最大堆、最大堆的应用及其python实现
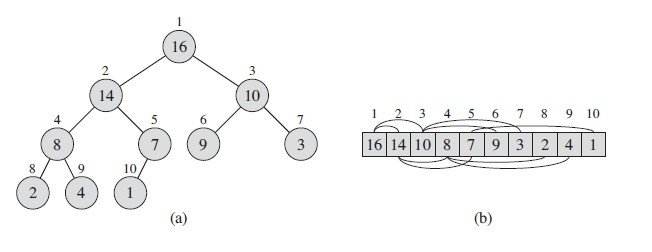
堆是一个数组,它可以被看成一个近似的完全二叉树,树上的每一个节点对应数组的一个元素。除了最底层外,该树是完全充满的,而且是从左到右填充的。
堆一般可以分为两种形式:最大堆和最小堆。最大堆是指,根节点的值大于其孩子节点的值;最小堆是指,根节点的值小于其孩子节点的值。
A.length表示数组元素的个数,A.heap-size表示有多少个堆元素,left表示i节点的左节点,如下图所示,left = 2*i,同理right = 2*i+1
堆的一些基本过程:
1.堆的维护:
假如下图的根节点不是16而是0,那么这显然违反了最大堆的性质,这时候需要让该元素在最大堆中逐级下降,维护最大堆的性质。
其伪代码为:
MAX—HEAPIFY(A,i)
1 L = left(i)
2 R = right(i)
3 if L<=A.heap-size and A[L]>A[i]
4 largest = L
5 else largest = i
6 if R<=A.heap-size and A[R]>A[largest]
7 largest = R
8 if largest != i
9 exchange A[i] and A[largest]
10 MAX-HEAPIFY(A2.堆的建立
可以自底向上的方法利用堆的维护过程把一个大小n = A.length的数组转化为最大堆。
因为数组A(n/2+1,...,n)的所有元素都在输的叶节点中,因此可以看成只包含一个元素的堆,因此,只需要对其他的节点调用MAX-HEAPIFY即可。
伪代码:
BUILD-MAX-HEAP(A)
1 A.heap-size = A.length
2 for i = A.length/2 downto 1
3 MAX-HEAPIFY(A,i)3.堆排序算法
初始的时候,堆排序利用堆的建立过程,建立最大堆,因此,数组的最大元素处于根节点的位置,也就是A[1],通过把它与A[n]交换,可以让最大元素处于正确的位置。这个时候,从堆中去掉该元素,对剩下的n-1个元素利用对的维护过程,建立大小为n-1的最大堆。如此重复,知道堆的大小降到2,完成了排序。
伪代码:
HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i = A.length downto 2
3 exchange A[1] with A[i]
4 A.heap-size = A.heap-size - 1
5 MAX-HEAPIFY(A,1)4.堆排序的python实现
def heap_adjust(A,i,size):
left = 2*i+1
right = 2*i+2
max_index = i
if(left5.利用堆获取 top K
问题描述:有N(N>>10000)个整数,求出其中的前K个最大的数。(称作Top k或者Top 10)
思路分析:
方法一:我们首先会想到排序(外排):因为是N个数据,并且N个数据是比较大的,有的读者可能会想到用数组进行存储,但是当数据非常大的时候,内存会不足,我们总不可能要买内存吧。但是外排是在磁盘上的,效率会很低。时间复杂度是Nlg(N).
方法二:利用堆来进行实现
*我们首先建立一个K大小的堆,
*接着,我们是要找最大的前K个数,我们应该建大堆还是小堆呢,可能很多读者会不假思索的说建大堆,但是我们来仔细的考虑下,如果建大堆的话,堆顶的元素就是最大的,那么后面的元素就进不来了,只会找到一个最大的元素,所以我们要建小堆。
*我们建好堆后,每次将来的一个元素和堆顶的元素进行比较,如果大于堆顶的元素的话,那么我们就将此元素直接赋给堆顶的元素。然后进行向下调整。
给出python实现的代码:
###最小堆实现topK
def heap_adjust(A,i,size):
left = 2*i+1
right = 2*i+2
min_index = i
if(leftA[left]):
min_index = left
if(rightA[right]):
min_index = right
if(min_index!=i):
temp = A[min_index]
A[min_index] = A[i]
A[i] = temp
heap_adjust(A,min_index,size)
return A
def build_heap(A,size):
for i in range(int(size/2),-1,-1):
heap_adjust(A,i,size)
return A
arr = [1,2,3,4,5,6,7,8,9]
b = build_heap(arr[:3],3)
for i in range(3,len(arr)):
if(arr[i]>b[0]):
b[0] = arr[i]
b = heap_adjust(b,0,3)
print(b) 由于仅仅保存了K个数据,调整最小堆的时间复杂度为O(lnK),因此top K算法(问题)时间复杂度为O(nlnK).
参考文献:
1.算法导论第3版(Introduction to Algorithms - Third Edition)
2.《数据结构::堆及堆的应用~》https://blog.csdn.net/lalu58/article/details/53954465
3.《海量数据处理的 Top K算法(问题) 小顶堆实现》https://www.cnblogs.com/xudong-bupt/archive/2013/03/20/2971262.html