GNNExplainer: Generating Explanations for Graph Neural Networks 个人总结
GNNExplainer: Generating Explanations for Graph Neural Networks 个人总结
写在前面:为方便阅读,尽量使用中文总结,对于翻译无把握或专有词汇,在中文后附上原文字段。此外,水平有限,对文章理解有偏差部分恳请大家海涵, 指正。
0. 原作信息
@inproceedings{ying2019gnnexplainer,
title={Gnnexplainer: Generating explanations for graph neural networks},
author={Ying, Zhitao and Bourgeois, Dylan and You, Jiaxuan and Zitnik, Marinka and Leskovec, Jure},
booktitle={Advances in Neural Information Processing Systems},
pages={9240--9251},
year={2019}
}
1. Contribution 本文贡献
-
提出第一款通用,模型无关的(model-agnostic)对于GNN模型的解释器GNNEXPLAINER
-
形式化描述GNNEXPLAINER为最大化互信息的优化任务
-
抽取重要的子图结构及节点特征子集,作为模型解释。
2. Background 背景信息
对于非图结构的神经网络,解释方法主要有如下两个方向:
- 为整个网络构建简单的代替模型
常为模型无关的(model-agnostic),在待解释样本点的局部建立可信的估计。
E.g., 线性模型如LIME,规则集合如ANN_DT
- 识别模型计算过程中的重要层面
E.g. 关注特征梯度(feature gradients)等。
对于图神经网络设计解释方法,除去节点特征外,还需要结合考虑图的结构特征。
3. Problem Formulation 问题定义
3.1 GNN回顾
抽象GNN基本操作如下:
给定GNN模型 Φ \Phi Φ , 对于 l l l 层节点 v v v的特征表达求取,共经过如下3步。
-
与其邻居节点进行信息传递:
m i j l = MSG ( h i l − 1 , h j l − 1 , r i j ) m_{i j}^{l}=\operatorname{MSG}\left(\mathbf{h}_{i}^{l-1}, \mathbf{h}_{j}^{l-1}, r_{i j}\right) mijl=MSG(hil−1,hjl−1,rij)
-
聚合邻居节点信息:
M i l = AGG ( { m i j l ∣ v j ∈ N v i } ) M_{i}^{l}=\operatorname{AGG}\left(\left\{m_{i j}^{l} | v_{j} \in \mathcal{N}_{v_{i}}\right\}\right) Mil=AGG({mijl∣vj∈Nvi})
-
结合自身节点上层表达,生成本层节点表达
h i l = UPDATE ( M i l , h i l − 1 ) \mathbf{h}_{i}^{l}=\operatorname{UPDATE}\left(M_{i}^{l}, \mathbf{h}_{i}^{l-1}\right) hil=UPDATE(Mil,hil−1)
3.2 GNNEXPLAINER: Problem formulation
对于节点 v v v,其经过图神经网络后得到的embedding,由其对应的邻居节点及特征决定,分别计邻居组成的子图结构为 G c ( v ) G_{c}(v) Gc(v),特征集合为 X c ( v ) X_{c}(v) Xc(v),
则节点的预测输出为
y ^ = Φ ( G c ( v ) , X c ( v ) ) \hat{y}=\Phi\left(G_{c}(v), X_{c}(v)\right) y^=Φ(Gc(v),Xc(v))
解释器GNNEXPLAINER目标,即是提取出具备解释性的子图、特征子集 ( G S , X S F ) \left(G_{S}, X_{S}^{F}\right) (GS,XSF)
具象化表示为下图:
4. GNNEXPLAINER
一系列公式推导,说明如何提取子图、子特征。
4.1 单一样本的解释 Single-instance explanations
设节点 v v v的子图为 G S G_S GS,有 G S ⊆ G c G_{S} \subseteq G_{c} GS⊆Gc,对应的有特征子集 X S = { x j ∣ v j ∈ G S } X_S=\left\{x_{j} | v_{j} \in G_{S}\right\} XS={xj∣vj∈GS}
我们想选取解释性的子图,则通过最大化互信息实现:
- max G S M I ( Y , ( G S , X S ) ) = H ( Y ) − H ( Y ∣ G = G S , X = X S ) \max _{G_{S}} M I\left(Y,\left(G_{S}, X_{S}\right)\right)=H(Y)-H\left(Y | G=G_{S}, X=X_{S}\right) maxGSMI(Y,(GS,XS))=H(Y)−H(Y∣G=GS,X=XS)
对于上式,由于GNN模型已经确定,故 H ( Y ) H(Y) H(Y)是常数。
展开第二项条件熵, H ( Y ∣ G = G S , X = X S ) = − E Y ∣ G S , X S [ log P Φ ( Y ∣ G = G S , X = X S ) ] H\left(Y | G=G_{S}, X=X_{S}\right)=-\mathbb{E}_{Y | G_{S}, X_{S}}\left[\log P_{\Phi}\left(Y | G=G_{S}, X=X_{S}\right)\right] H(Y∣G=GS,X=XS)=−EY∣GS,XS[logPΦ(Y∣G=GS,X=XS)],为了求解一个紧致解,我们约束 ∣ G S ∣ ≤ K M \left|G_{S}\right| \leq K_{M} ∣GS∣≤KM,可以理解为降噪,滤去无效邻居。
因而,我们得到:
- min G E G S ∼ G H ( Y ∣ G = G S , X = X S ) \min _{\mathcal{G}} \mathbb{E}_{G_{S} \sim \mathcal{G}} H\left(Y | G=G_{S}, X=X_{S}\right) minGEGS∼GH(Y∣G=GS,X=XS)
基于Jensen不等式,假设为凸函数,我们能得到上界:
- min G H ( Y ∣ G = E G [ G S ] , X = X S ) \min _{\mathcal{G}} H\left(Y | G=\mathbb{E}_{\mathcal{G}}\left[G_{S}\right], X=X_{S}\right) minGH(Y∣G=EG[GS],X=XS)
有意思的地方来了,作者大意是:效果很好,原理就别纠结了直接用就是。
显然,GNN是不满足凸函数假设的,但工作中发现基于上述目标函数,结合正则项,对于所学的局部最优解已经有较好的解释能力。
对于期望 E G [ G S ] \mathbb{E}_{\mathcal{G}}\left[G_{S}\right] EG[GS],通过一个掩码来实现, A c ⊙ σ ( M ) , A_{c} \odot \sigma(M), Ac⊙σ(M), where M ∈ R n × n M \in \mathbb{R}^{n \times n} M∈Rn×n。即,实际解释器要学习的,即是掩码M。
进一步,一般我们希望了解“此样本为何被预测为某一个类别”,而不是对全局模型的理解。故进一步修改目标函数为:
- min M − ∑ c = 1 C 1 [ y = c ] log P Φ ( Y = y ∣ G = A c ⊙ σ ( M ) , X = X c ) \min _{M}-\sum_{c=1}^{C} \mathbb{1}[y=c] \log P_{\Phi}\left(Y=y | G=A_{c} \odot \sigma(M), X=X_{c}\right) minM−∑c=1C1[y=c]logPΦ(Y=y∣G=Ac⊙σ(M),X=Xc)
4.2 节点特征选择 Node feature information
同理,也使用掩码实现。
X S F = { x j F ∣ v j ∈ G S } , x j F = [ x j , t 1 , … , x j , t k ] X_{S}^{F}=\left\{x_{j}^{F} | v_{j} \in G_{S}\right\}, \quad x_{j}^{F}=\left[x_{j, t_{1}}, \ldots, x_{j, t_{k}}\right] XSF={xjF∣vj∈GS},xjF=[xj,t1,…,xj,tk] for F t i = 1 F_{t_{i}}=1 Fti=1
综上,对于整个解释器,要优化的目标函数即是:
max G S , F M I ( Y , ( G S , F ) ) = H ( Y ) − H ( Y ∣ G = G S , X = X S F ) \max _{G_{S}, F} M I\left(Y,\left(G_{S}, F\right)\right)=H(Y)-H\left(Y | G=G_{S}, X=X_{S}^{F}\right) maxGS,FMI(Y,(GS,F))=H(Y)−H(Y∣G=GS,X=XSF)
此外,paper中提到使用reparametrization的trick来学习参数掩码。
除却上述目标函数外,解释器还加入若干正则项限制,如
- element-wise entropy,鼓励掩码离散
- 惩罚过多非零项的掩码
4.3 样本子集的解释 Multi-instance explanations through graph prototypes
未完全看懂。
除了对于单个样本的解释,GNNEXPLAINER也能对样本子集进行解释,如给出某类样本的解释。
实现思路,个人理解为“想办法将问题转化为单样本的解释。故需要设计算法实现代表节点的创建及响应的邻接矩阵生成”。
基本步骤有2:
- 选择参考节点(可通过对节点子集embeddings求平均实现)
- 创建对应的邻接矩阵
5. Experiments 实验
实验设计、呈现都很巧妙,值得分析学习。
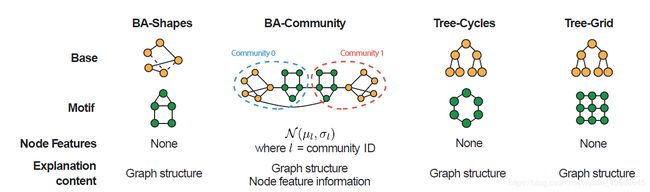
5.1 数据集
5.2 Baselines
做一个迁移当baselines。
- GRAD,基于梯度。
- ATT,使用GAT中的注意力权重。
5.3 Results 结果
-1. One More Thing
个人思考:
对于单样本的输出解释,若是做一个模型无关的解释器,如下两个步骤的设计是关键:
-
采样。
对于GNN这样基于消息传递的模型,每个节点的输出肯定受其邻居节点的影响。如何有效采样,构建子图,值得考量。
-
目标函数设计。
如何设计一个目标函数?本篇工作使用最大化互信息,还可以设计别的吗,如何优化?
扩展阅读:
- LIME
- GraphLIME
参考资料:
略去了文章中关于平均场部分,相关数据知识补充在此:
- 平均场近似
- 各种熵的理解