Python 刷题笔记:二叉树专题一
今天来看二叉树专题,首先我们先整理下基础知识点;基于在 LeetCode 推荐题解中发现的一个适用于二叉树遍历的套路解法,我们今天也会连刷三道关于前序、中序和后序遍历的题目。
这个改变对二叉树认知的神奇解法,真的非常值得一看!
基础知识点
树
首先看下“树”的概念:
树是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由 n(n>0) 个有限节点组成一个具有层次关系的集合。
链接:https://leetcode-cn.com/tag/tree/
来源:力扣(LeetCode)
之所以把它称为树,是因为它形似一棵倒着的树,由一个根不断拓展出枝桠。
二叉树
二叉树就是一种使用普遍的树结构:
在计算机科学中,二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
维基百科-二叉树
这里我们举一个二叉树的例子:
示例来源:
https://blog.csdn.net/google19890102/article/details/53926704
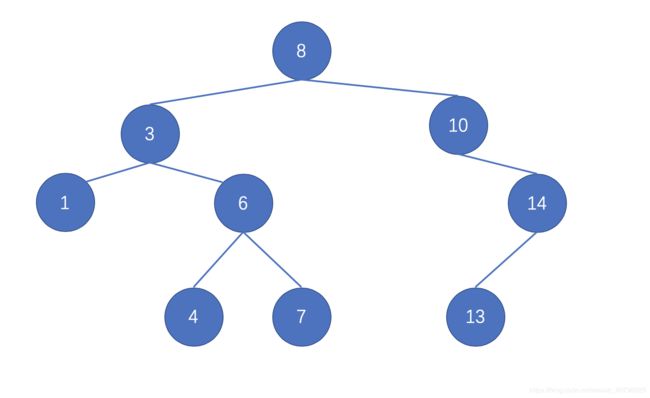
图是用 ppt 做的,有些简陋,以最上面的 8 为根节点,那么其左侧分支即左子树、右侧分支即右子树;我们把 3 称为根节点 8 的左子节点、10 为其右子节点。
那么我们可以发现,图里最左侧的 1 节点没有子节点了,可以把它称之为叶子节点,以及最右侧的 14 节点只有一个左子节点——这是一棵并不圆满的二叉树。
这样我们可以得出“圆满的二叉树”即满二叉树的定义:
如果每一个非叶子节点都存在左右子树,并且二叉树中所有的叶子节点都在同一层中,这样的二叉树称为满二叉树。
二叉树的表示
除了用图来展示,放到代码里我们怎么表示二叉树呢?通常有两种方法:
- 顺序存储结构
从上至下、由左及右,将所有节点值填入一维数据(比如列表)中,若某位置节点缺失,可以填充 None,所以上图中的二叉树我们可以记为:
[8,3,10,1,6,None,14,None,None,4,7,None,None,13,None]
- 链式存储结构
定义节点类,在其属性中定义左子节点、右子节点以及该节点值:
# Definition for a binary tree node.
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
二叉树遍历
我们可以看到,在顺序存储结构中,可能会充斥大量的 None 空节点,这些其实是用不到的数据,所以在二叉树遍历时,有如下几种遍历模式,它们按照固定的顺序只遍历非空的节点:
- 前序遍历
按照 根节点 - 左子树 - 右子树 的顺序遍历,结合刚二叉树例子,如图:
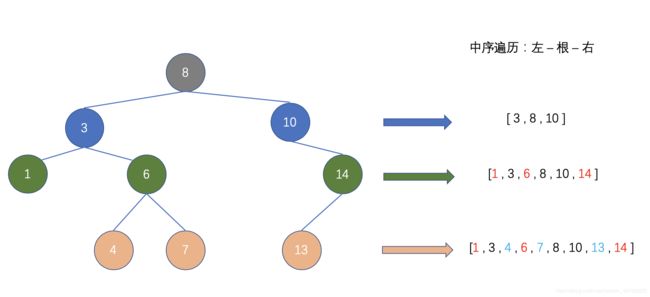
- 中序遍历
按照 左子树 - 根节点 - 右子树 的顺序遍历:
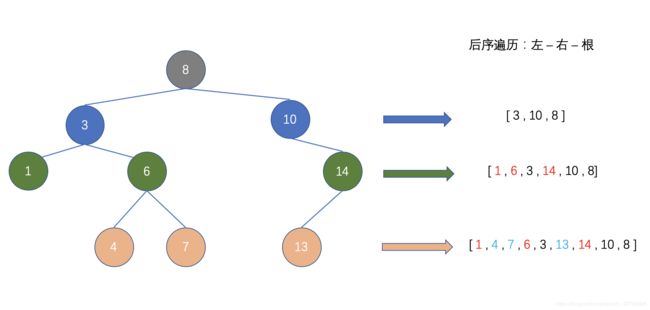
- 后序遍历
按照 左子树 - 右子树 - 根节点 顺序遍历:
此外,还有层次遍历,即按从上至下、从左到右每层遍历得到 [ 8 , 3 , 10 , 1 , 6 , 14 , 4 , 7 , 13 ]
代码套路解法
回顾上面三种遍历二叉树的过程,其实每次都是用特定的顺序继续填充子树数据到节点附近,那么在代码中如何实现呢?这里就给大家推荐这个作者自称为“颜色标记”的方法。
解法来源:
https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/yan-se-biao-ji-fa-yi-chong-tong-yong-qie-jian-ming/
这里以中序遍历即左 - 根 - 右 顺序遍历代码为例,首先会设定 white、gray 两种颜色,用处是用来区分此时节点是否作为结果输出、还是要继续填充子树数据信息。每个节点都会与颜色组成元组存入一个暂存栈 stack 中,后进先出,从栈中取出节点后依据其颜色判断是否继续存入子树信息还是要输出节点信息。
中序遍历为 左 - 根 - 右 顺序,那么存入栈时顺序要反着来,这样在后进先出的原则下才能达到中序规则,具体代码如下:
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
# 两种颜色标记状态
WHITE, GRAY = 0, 1
# 用来输出结果的列表
res = []
# 暂存节点的栈
stack = [(WHITE, root)]
# 栈不为空
while stack:
# 提取栈中最新的元素
color, node = stack.pop()
# 如果节点为空,继续下一循环
if node is None: continue
# 如果为白色,要继续将节点数据存入栈中
if color == WHITE:
# 注意,这里存入的顺序是中序 左-根-右 的相反顺序
# 先右节点,搭配白色
stack.append((WHITE, node.right))
# 再根节点,搭配灰色
stack.append((GRAY, node))
# 最后左节点,搭配白色
stack.append((WHITE, node.left))
# 若颜色为灰色
else:
# 将节点值添加到结果列表中
res.append(node.val)
# 返回结果列表
return res
#作者:hzhu212
#链接:https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/yan-se-biao-ji-fa-yi-chong-tong-yong-qie-jian-ming/
这段代码,如果干看不好理解的话,以我们之前的例子来逐步分解参考:
最初的根节点 8,其左子节点 3、右子节点 10,最初 stack 中存的是 ( 白色 0,根节点 8);
栈非空进入循环,从 stack 中提取出( 白色 0,根节点 8)赋值给 color 和 node,此时颜色为白色,便将根节点附近左右子节点数据按照中序倒序存入 stack 中;
继续提取 stack 中元素,此时提取的顺序是按照中序正常顺序了,继续根据颜色判断是否要继续扩展子节点数据,若否,则会逐步将节点值添加到结果中。
以上代码如果能够理解,那么,接下来三道针对不同二叉树遍历的题目,只需要调整下存入 stack 时节点的先后顺序,便可轻松解决了!
题目一
第 144 题:二叉树的前序遍历
难度:中等
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,2,3]
题目分析
前序排列是 根 - 左 - 右 的顺序,那么将套路代码中入栈顺序改为 右 - 左 - 根,即可完成任务,只要能记住刚刚大致逻辑,便可自行写出如下代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
white,gray = 0,1
res = []
stack = [(white,root)]
while stack:
color,node = stack.pop()
if node == None:
continue
if color == white:
# 区别在这,根-左-右 前序的相反 右-左-根
stack.append((white,node.right))
stack.append((white,node.left))
stack.append((gray,node))
else:
res.append(node.val)
return res
提交测试表现:
执行用时 : 32 ms, 在所有 Python3 提交中击败了 92.57% 的用户
内存消耗 : 13.7 MB, 在所有 Python3 提交中击败了 7.14% 的用户
题目二
第 94 题:二叉树的中序遍历
难度:中等
给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
题目分析:
就是我们套路代码展示的例子,这次我们独立默写:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
white,gray = 0,1
res = []
stack = [(white,root)]
while stack:
color,node = stack.pop()
if node==None:
continue
if color==white:
# 中序倒序
stack.append((white,node.right))
stack.append((gray,node))
stack.append((white,node.left))
else:
res.append(node.val)
return res
提交测试表现:
执行用时 : 40 ms, 在所有 Python3 提交中击败了 61.12% 的用户
内存消耗 : 13.6 MB, 在所有 Python3 提交中击败了 7.84% 的用户
题目三
第 145 题:二叉树的后序遍历
难度:困难
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
题目分析
当同一份代码写三遍,下次遇到应该出不了错了!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
white,gray = 0,1
res = []
stack = [(white,root)]
while stack:
color,node = stack.pop()
if node is None:
continue
if color==white:
# 区别在这,后序倒序
stack.append((gray,node))
stack.append((white,node.right))
stack.append((white,node.left))
else:
res.append(node.val)
return res
提交测试表现:
执行用时 : 36 ms, 在所有 Python3 提交中击败了 79.41% 的用户
内存消耗 : 13.7 MB, 在所有 Python3 提交中击败了 7.41% 的用户
结论
因为一个解题套路,LeetCode 三连斩,还有比这更爽的么?借助这个解法,我们也能大致理解整个代码的设计思路,通过练习熟悉掌握这解法。当然,还有很多其它更抓问题本质的解法,但说实话、新手不友好,配合着其各种术语,可能这次勉强理解,但下次写的时候便忘掉甚至混淆了。所以,这里还是表达对这个解法的赞赏、仰慕和推荐!
基于这三个题目练习,我们对二叉树的前序遍历、中序遍历和后序遍历应该是可以轻松掌握了。明天我们再琢磨二叉树相关的其它知识点和题目~