数学建模之十分钟学会LINGO(附建模实战)
Lingo 基本界面
- 打开lingo后会弹出一个对话框,点击 Cancel 左边的 Never Register 即可,其余内容用不到。
- 界面自动弹出名为“Lingo Model – Lingo 1”的窗口,用于书写代码。
- 以解方程的题目: x + 1 = 2 x+1=2 x+1=2为例,写完代码后,点击“红色的靶心”运行程序。
- 首先 Lingo 会弹出一个名为“Solver Status”的对话框,它显示运行时间等信息。读取到运行时间是 0 时 0 分 0 秒,充分证明了 Lingo 的强大之处。

5. 然后,弹出一个名为“Solution Report”的界面。
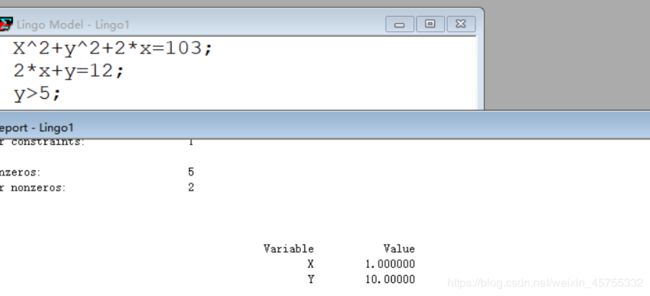
6. 由此可知变量 x 的数值为 1。
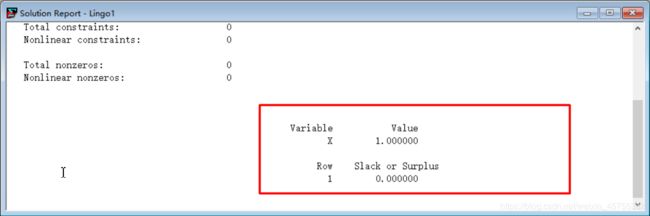
7. 如果是求解线性规划的话,目标值也会在“Solution Report”中给出,到时再说。
用 Lingo 解方程
① 每个方程必须以分号“;”结束。
② 请注意:Lingo 的所有符号都是英文格式下的符号。
③ Lingo 的加减乘除分别是: + − ∗ / + - * / +−∗/。
【特别注意】
(1) 2 ∗ x 2*x 2∗x 在 Lingo 中不可以简写为 2 x 2x 2x ,乘号不能省略。
(2) 注意除号“/”的形状
【例题】求解方程组
2 ∗ x + 2 ∗ y + 1 = 5 3 ∗ x − 5 ∗ y + 5 = 3 2*x+2*y+1=5\\ 3*x-5*y+5=3 2∗x+2∗y+1=53∗x−5∗y+5=3
【易错点】
① 不写结尾的分号。
② 不写乘号。
Lingo 变量
- Lingo 默认所有变量为大于等于 0 的数字,因而非负的条件不必多写。
- 万一遇到一个变量可以小于 0,后面会讲到一个函数叫做@free,来使其定义域为 R。
- m 和 M 等价,Lingo 不区分大小写,所以 mmm、mMm、MMM 被视作同一个变量。
- 无论是 C、Matlab 还是 Lingo,变量均由字母数字下划线组成,且字母在首位。
【例题】求解方程组:
X 2 + y 2 + 2 ∗ x = 103 2 ∗ x + y = 12 x > 0 y > 5 X^2+y^2+2*x=103\\ 2*x+y=12\\ x>0\\ y>5 X2+y2+2∗x=1032∗x+y=12x>0y>5
线性规划基础
① 一个线性规划中只含一个目标函数。(两个以上是多目标线性规划,Lingo 无法直接解)
② 求目标函数的最大值或最小值分别用 max = …或 min = …来表示。
③ 以 !开头,以 ;结束的语句是注释语句;
④ 线性规划和非线性规划的本质区别是目标函数是否线性,其余一致,故不需要区分。
但值得注意的是,非线性规划的求解十分困难,基本得不到全局最优解。
矩阵工厂
矩阵工厂:生产一维矩阵
先来看看例子,当然不必在意其中的空格(Lingo 不读取空格):
sets:
factory /1..6/ : a,b;
plant /1..3/ : x,y;
endsets
以上程序对应知识点:
① factory 和 plant 都是制造矩阵的工厂,但它们是两家不同的工厂。
② factory 工厂后面的 /1…6/ 说明它专门生产 1 ∗ 6 1*6 1∗6 的矩阵。
factory 工厂最后面出现的 a 和 b,都是 1 ∗ 6 1*6 1∗6的矩阵。
③ plant 工厂后面的 /1…3/ 说明它专门生产 1 ∗ 3 1*3 1∗3 的矩阵。
plant 工厂最后面出现的 x 和 y,都是 的矩阵。
④ 矩阵工厂的名字 factory 是随便起的,工厂所生产行矩阵的名字 a 和 b 也是随便起的。
⑤ 以上这四句话,本质是定义了四个行矩阵的大小,矩阵工厂只是中介。
⑥ 生产完矩阵后,工厂和矩阵之间将脱开联系。
⑦ Lingo 不是一行一行读代码的,所以用 sets:和 endsets 表示矩阵工厂生产流程的起止。
【例 】阅读以下 Lingo 代码,请问 a 和 b 两个矩阵有联系吗?
sets:
nanfu /1..6/ : a,b;
endsets
没有特殊联系,只是 a 和 b 都是一行六列的矩阵。
【例 】阅读以下 Lingo 代码,请问代码可否简洁一点?
sets:
ctgu /1..6/ : a;
mcm /1..6/ : b;
endsets
a,b可以合并
sets:
easy /1..6/ : a, b;
endsets
【例 3】阅读以下 Lingo 代码,请问有何问题?
sets:
ceshi /1..6/ : apple, Apple;
endsets
Lingo 不区分大小写,所以 apple 和 Apple 是同一个矩阵,应该换个名字。
矩阵的赋值
矩阵工厂不能只生产矩阵,还要给矩阵赋初值才行,例子如下:
sets:
factory /1..6/ : a,b;
plant /1..3/ : c,x;
endsets
data:
a = 1, 2, 3, 4, 5, 6;
b = 6.0, 5.0, 4.0, 3.0, 2.0, 1.0;
c = 10, 20, 30;
enddata
以上程序对应以下知识点:
① 不是每个矩阵都要赋值,有些矩阵正是我们要求解的变量。
② 需要赋值的矩阵必须赋满,不能给 6 个元素的矩阵只赋 3 个数值。
③ Lingo 中可以给矩阵赋整数,也可以赋小数。
④ Lingo 不是一行一行读代码的,所以用 data:和 enddata 表示矩阵赋值的起止。
循环与求和

【for 循环】
题中约束条件: S = a i x i , i = 1 , 2 , . . . 5 S=a_ix_i,i=1,2,...5 S=aixi,i=1,2,...5 可以利用 for 循环一步到位。
@for( gc(i) : a(i)*x(i) = S );
① for 循环,括起整行语句,因为 S = a i x i , i = 1 , 2 , . . . 5 S=a_ix_i,i=1,2,...5 S=aixi,i=1,2,...5 相当于 5 个约束条件:
S = a 1 x 1 . . . S = a 5 x 5 S=a_1x_1\\ .\\.\\.\\ S=a_5x_5 S=a1x1...S=a5x5
② for 循环内部,先写工厂,以告诉 for 循环几次,之后再上接约束条件。
③ 此处的 i 可带可不带,甚至可以换成 j、k 或 m 等等。
④ 二维矩阵工厂出现后,同时会出现 i 和 j,那时必须带 i 和 j。
【sum 求和】
题中约束条件: ∑ i = 1 5 = 5000 \sum_{i=1}^{5}=5000 ∑i=15=5000可以利用 sum 求和一步到位。
@sum( gc(i) : x(i) ) = 5000;
① sum 求和,不可以括起完整的约束条件,因为一般的求和的结构是这样的: x 1 + . . . + x 5 = 5000 x_1+...+x_5=5000 x1+...+x5=5000
② sum 求和内部,先写工厂,以告诉 sum 求和几次,之后再上接约束条件。
③ 此处的 i 可带可不带。
④ 二维矩阵工厂出现后,同时会出现 i 和 j,那时必须带。
【for 与 sum 出现的标志】
① 约束条件后面有 i = 1 , 2 , . . 5 i=1,2,..5 i=1,2,..5,一定在最外层套上 for。
② 约束条件前面是 ∑ i = 1 5 \sum_{i=1}^{5} ∑i=15 ,一定在中间加sum
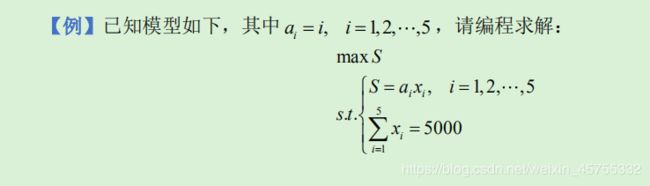
程序自己打一遍才会理解

model:
sets:
gc /1..5/ : a,x;
endsets
data:
a = 1,2,3,4,5;
enddata
max = S;
@for( gc(i) : a(i)*x(i) = S );
@sum( gc(i) : x(i) ) = 5000;
end
工厂合并
工厂合并——生产二维矩阵
先来看看例子:
sets:
factory /1..6/ : a;
plant /1..8/ : d;
Cooperation(factory,plant) : c, x;
endsets
以上程序可以得到以下结论:
① Cooperation 大工厂是由 factory 和 plant 两家小工厂合并而办,可生产 6x8的矩阵。
② a 是1x6 的矩阵,d 是1x8 的矩阵,c 和 x 都是4x8 的矩阵。
③ 如果将 Cooperation(factory,plant)中的 factory 与 plant 调换位置,则生产 8x6的矩阵。
④ 工厂合并的名字 Cooperation 是随便起的,矩阵的名字 c 和 x 也是随便起的。
矩阵的赋值
data:
c=6,2,6,7,4,2,5,8
4,9,5,3,8,5,8,2
5,2,1,9,7,4,3,3
7,6,7,3,9,2,7,1
2,3,9,5,7,2,6,5
5,5,2,2,8,1,4,3;
enddata
model:
sets:
factory /1..6/ : a;
plant /1..8/ : d;
Cooperation(factory,plant) : c, x;
endsets
data:
a=60,55,51,43,41,52;
d=35,37,22,32,41,32,43,38;
c=6,2,6,7,4,2,5,8
4,9,5,3,8,5,8,2
5,2,1,9,7,4,3,3
7,6,7,3,9,2,7,1
2,3,9,5,7,2,6,5
5,5,2,2,8,1,4,3;
enddata
min = @sum( Cooperation(i,j) : c(i,j)*x(i,j) );
@for( factory(i): @sum(plant(j):x(i,j)) <= a(i) );
@for( plant(j): @sum(factory(i):x(i,j)) = d(j) );
end
本篇博客主要参考与[B站爆肝杰哥](https://space.bilibili.com/358229576?spm_id_from=333.788.b_765f7570696e666f.2)
弄懂上面那个例题建模题基本就差不多了,但我们的最终目的还是建模应用,这里没有具体的讲解求解窗口各个值的含义,具体线性规划建模实战可以看这里