GeniePath：Graph Neural Networks with Adaptive Receptive Paths 论文详解 KDD 2018

论文：GeniePath: Graph Neural Networks with Adaptive Receptive Paths
一种自适应感知路径的GNN：GeniePath

作者：蚂蚁金服的刘子奇、陈超超、李龙飞、周俊、李小龙、宋乐等人

来源：KDD 2018
KDD的全称是ACM SIGKDD Conference on Knowledge Discovery and Data Mining

论文链接：https://arxiv.org/abs/1802.00910

github链接：无

GeniePath，一种可扩展的能够学习自适应感受路径的图神经网络框架。它定义在具有排列不变性的图数据上（permutation invariant graph data）。它的自适应路径层（adaptive path layer）包括两个互补的功能单元，分别用来进行广度与深度的探索，前者用来学习一阶邻居节点的权重，后者用来提取和过滤高阶邻居内汇聚的信息。在直推（transductive）和归纳（inductive）两种学习任务的实验中，在大型图上均达到了 state-of-the-art 的效果。

1 相关介绍

图数据是不规则的，非欧氏距离的，图中的每个顶点的感受野都不同。
这篇文中定义的感受野（receptive field）：图中一个节点的感受野为包含从这个节点出发到目标节点的路径上的所有节点构成的子图。

考虑一个经典的GCN网络
$$H^{(t+1)}=\sigma \left(\varphi (A)H^{(t)}{W}^{(t)}\right)$$
其中

• $H^{(t)}\in {\mathbb{R}}^{N\times K}$为第$t$层N个节点的中间embedding
• 对$T$层的GCN网络，$T$决定了利用了多少邻居节点
• 任何两个节点的最短路径$d$都满足$d(i,j)\le T$（文中的意思就是对于一个$T$层的网络，只有距离节点$i$不超过$T$的节点$j$对节点$i$的embedding有贡献)

1.1 感受野的定义

• 基于谱域的图卷积网络通过拉普拉斯矩阵为每个节点定义邻居的重要性，因此邻居就是感受野。
• 基于空间域的图卷积网络的感受野或多或少都通过手动定义，比如GraphSage中用节点的固定size的邻居的均值或最大值定义感受野，或用一个需要预先选择邻居节点顺序的LSTM聚合器定义感受野。

上述两种定义方式都限制了在图中找到一种有意义的自适应的感受野。例如简单堆叠多层GCN(Kipf
and Welling 2016)使得感受野变大或路径变深，但是性能会急剧下降。（一些论文中使用残差连接使得性能稍有提升）

此文解决了下面两个没有解决的问题：

• 在图卷积中是否存在一条对表示最有贡献的路径？
• 在图卷积网络中是否存在一种自适应、能自动选择感受野或路径的方式？

贡献

（1）构造了排列不变性的图数据的函数空间，其中任何符合条件的聚合函数都应该满足这个空间
（2）提出了由两部分构成的能自适应的路径层：

• 能适应广度的函数：能够自动选择重要性最大的one-hop邻居
• 能适应深度的函数：可以提取和过滤有用的、有噪声的的信号

（3）在Pubmed、BlogCatalog、Alipay dataset数据集上进行实验，实验结果表明GeniePath算法的有效性，在大图上有state-of-the-art的效果。此外，GeniePath对卷积层的深度不是很敏感，可以考虑GCN的加深。

文中提出了一个自适应路径层，可以指导感受野的深度和广度的探索，并把这种自适应学习的感受野命名为感受路径。

2 图卷积网络GCN

GCN、GraphSAGE、GAT

将卷积推广到图上的目的是用感受野中的信号编码节点。输出编码的embedding，然后可以进一步用于端到端的半监督学习(Semi-supervised classification with graph convolutional networks)或者非监督学习任务(Deepwalk: Online learning of social representations)

下面分别介绍了：
Kipf and Welling (2016)的GCN，可以参考：
论文详解：Semi-Supervised Classification with Graph Convolutional Networks用图卷积进行半监督分类

介绍了GraphSAGE，可以参考：
论文详解：GraphSAGE：Inductive Representation Learning on Large Graphs

介绍了Graph Attention Networks (GAT)，可以参考：
论文详解：Graph Attention Network (GAT) 图注意力网络 论文详解 ICLR2018

Discussions

上面的这些网络的主要工作都是设计有效的聚合器函数，使得可以在每个节点的T-th邻居周围传播信号。但是很少有人试图研究指导传播有意义的路径问题。

为什么感受路径是重要的？

• graphs could be noisy
• 不同节点的感受路径不同

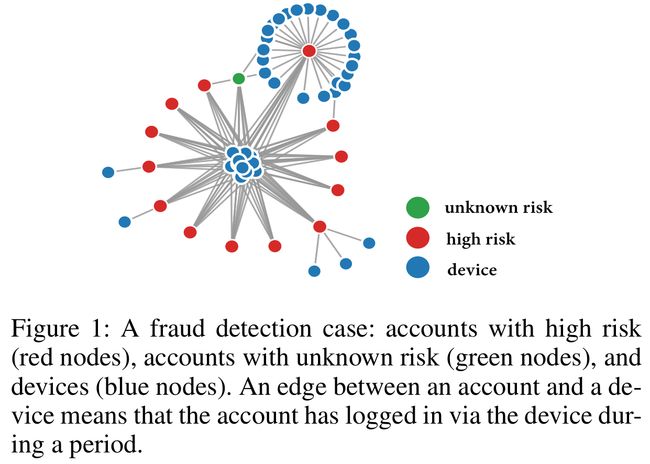
• 图1展示了诈骗数据的图模式
• 此图是一个二部图，图中有两种类型的节点：帐户和设备(例如IP代理)
• 红色表示恶意账户，恶意帐户倾向于聚合在一起，实际上，普通账号和恶意帐户可以连接到同一个IP代理。因此，不能简单地从图中看出标记为“绿色”的帐户是否是恶意的
• 根据每个节点的特征，可以验证此绿色账号是否与其他恶意账号具有类似的行为模式。因此，节点的特征可以作为额外的信息来细化邻居和路径的重要性

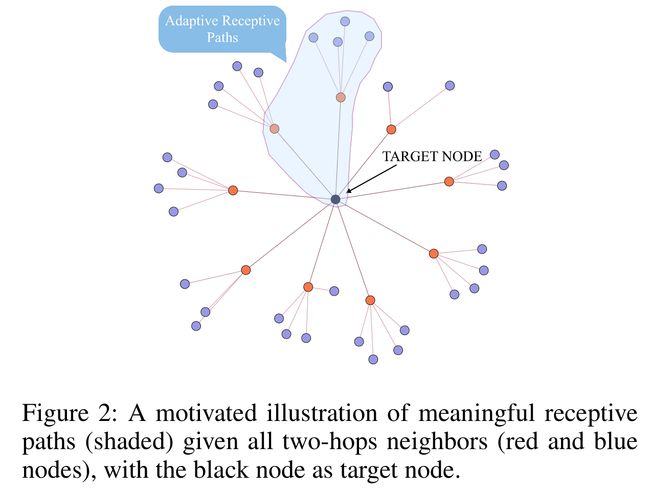
• 图2是一个以中心黑色的目标节点的two-hops邻居的自适应感受野路径的示意图
• 可以看出，图中阴影区域是文中认为的有意义的感受路径，而不是简单的对邻居信号进行聚合
• 其中有意义的路径可以看作是和目标节点相关的一个子图

现在，需要做的是广度/深度的探索和过滤有用的/有噪声的信号。广度的探索决定了哪些邻居是重要的，即引导探索的方向，而深度的探索决定了距离目标节点多少hop的邻居仍然有用。子图上的这种信号过滤本质上就是学习感受路径。

3 GeniePath

核心内容

• 讨论了满足图数据排列不变性要求的泛函空间
• 设计了具有学习图上“接受路径”的能力的神经网络层来满足这种要求

3.1 Permutation Invariant 排列不变性

排列不变性就是，输入参数顺序不影响输出结果的函数，如$f(a,b,c)=f(a,c,b)=f(b,a,c)$

函数空间要满足图数据所需要的排列不变性。要学的是一个函数$f$，将图 G 映射到embedding H。
假设作用在邻居上的（聚合）函数$f$具有排列不变性，学习任务与邻居节点的顺序是无关的，则在任何随机的排列$\sigma$下，下式都成立

$$f\left(\left\{h_1,\dots ,h_j,\dots \right\}|j\in \mathcal{N}(i)\right)=f\left(\left\{h_{\sigma (1)},\dots ,h_{\sigma (j)},\dots \right\}|j\in \mathcal{N}(i)\right),\text{\hspace{1em}(4)}$$

Theorem 1 (Permutation Invariant 排列不变性)

另一描述: 作用在节点$i$的邻居节点上的函数$f$满足排列不变性当且仅当$f$可以用映射$\varphi$和$\rho$分解成$\rho \left({\sum }_{j\in \mathcal{N}(i)}\varphi \left(h_j\right)\right)$。

定理1可以根据对称函数的基本定理(Zaheer et al. 2017)证明。

Remark 2 (Associative Property 结合律)

两个具有排列不变形的函数的复合函数$g\circ f$ 可以等价于$g(f(x))$,也是满足排列不变性的。

GraphSAGE 提供 LSTM 的聚合器，这种聚合器是不具有 Permutation Invariant 的，因为 LSTM 接收的是遍历节点的隐变量序列，排序是敏感的。此外，这里的 Permutation Invariant 也指图是静态的，不随时间演化。 因为文章中提到 “This is in opposition to temporal graphs.”

接下来，文中使用排列不变性的条件和结合律来设计传播层。

GeniePath算法的核心：当沿着已经学过的路径传播信号时学习感受路径，而不是根据预先定义的路径。这个问题就等价于对每一个节点通过广度（哪个one-hop邻居是重要的）和深度（邻居的重要性被忽略了）扩展检测一个子图。

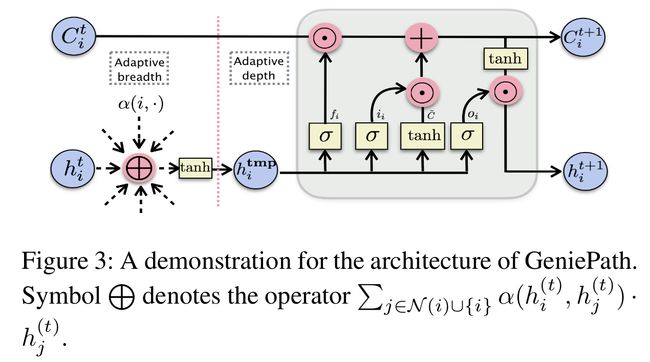
3.2 Adaptive Path Layer 自适应的路径层

Adaptive Path Layer 由Adaptive Breadth和Adaptive Depth 两个模块构成：

• Adaptive Breadth基于GAT学习一跳邻居（隐）特征的重要性，决定继续探索的方向
• Adaptive Depth 则是引入LSTM的长短记忆，保存和更新每一跳邻居信息：基于新观察到的邻居聚合信息$h_i^{(\mathrm{tmp})}$，更新门将新的有用信息加到到记忆中，遗忘门参考过滤掉无用的老记忆，故在探索更远的邻居时起到了选择抽取与过滤的作用。 并基于输出门和最新的记忆，输出节点$i$的第$t+1$层embeddng$h_i^{(t+1)}$

GeniePath算法如下

• 输入：深度$T$，节点的特征矩阵$H^{(0)}=X$，邻居矩阵$A$
• 输出：参数矩阵$\Theta ,\Phi$
• 自适应广度函数定义为：$H^{(tmp)}=\varphi \left(A,H^{(t-1)};\Theta \right)$
• 自适应深度函数定义为：$H^{(t)}=\phi (H^{(tmp)}|\{H^{(\tau )}|\tau \in \{t-1,\dots ,0\}\};\Phi )$
• 参数通过loss$\mathcal{L}\left(H^{(T)},\cdot \right)$进行反向传播优化

接下来需要具体化自适应的广度和深度函数，也就是$\varphi (\cdot )$和$\phi (.)$。

自适应路径层可以更具体的写为

$$h_i^{(\mathbf{t}\mathbf{m}\mathbf{p})}=\tanh \left({W^{(t)}}^{\top }\sum _{j\in \mathcal{N}(i)\cup \{i\}}\alpha \left(h_i^{(t)},h_j^{(t)}\right)\cdot h_j^{(t)}\right)\text{\hspace{1em}(5)}$$
其中

• ${W^{(t)}}^{\top }$是对加权聚合邻居的特征做线性转换，使之更强大
• $\alpha \left(h_i^{(t)},h_j^{(t)}\right)$即为线性attention操作，目的是学习节点$i$和邻居$j$的权重参数（基于它们的(隐)特征），结构如下（将节点（隐）特征$h_i$和$h_j$经线性转换后拼接，输入到一个NN神经元，用BP学习参数，softmax起归一化的作用）

那么
$$新增信号：\tilde{C}=\tanh \left({W_c^{(t)}}^{\top }{h}_i^{(\mathbf{t}\mathbf{m}\mathbf{p})}\right)$$

$$更新门:i_i=\sigma \left({W_i^{(t)}}^{\top }{h}_i^{(\mathbf{t}\mathbf{m}\mathbf{p})}\right)$$

$$遗忘门:f_i=\sigma \left({W_f^{(t)}}^{\top }{h}_i^{(\mathbf{t}\mathbf{m}\mathbf{p})}\right)$$
$$记忆更新：C_i^{(t+1)}=f_i\odot C_i^{\top }+i_i\odot \tilde{C}$$

$$O_i=\sigma \left({W_o^{(t)}}^{\top }{h}_i^{(\mathbf{t}\mathbf{m}\mathbf{p})}\right)$$

$$输出：h_i^{(t+1)}=o_i\odot \tanh \left(C_i^{(t+1)}\right)\text{\hspace{1em}(6)}$$

• 公式（5）对应于$\varphi (\cdot )$，剩余的门单元对应于$\phi (.)$
• 初始化$C_i^{(0)}\leftarrow 0\in {\mathbb{R}}^K$

在第$l+1$层，也就是在探索在$\{j|d(i,j)\le t+1\}$范围内的邻居时，有下面两个互补函数。

Adaptive breadth function

公式（5）通过线性attention操作$\alpha (\cdot ,\cdot )$对所有one-hop邻居的embedding$h_j^{(t)}$分配重要性

$$\alpha (x,y)={\mathrm{softmax}}_y\left(v^{\top }\tanh \left(W_s^{\top }x+W_d^{\top }y\right)\right),\text{\hspace{1em}(7)}$$
其中

$${\mathrm{softmax}}_{y}f(\cdot ,y)=\frac{\exp f(\cdot ,y)}{{\sum }_{y^{\prime }}\exp f\left(\cdot ,y^{\prime }\right)}$$

Adaptive depth function

A variant：GeniePath-lazy

先通过叠加Adaptive Breadth 函数传播T阶内的邻居信息，得到$\left\{h_i^{(0)},h_i^{(1)},\dots ,h_i^{(T)}\right\}$，再通过adaptive depth函数作用在它们上面进一步提取和过滤在不同深度层的信号。
初始化${\mu }_i^{(0)}=W_x^{\top }{X}_i$，并且${\mu }_i^{(T)}$放入最终的损失函数中。
输出$\left\{h_i^{(t)}\right\}$:
$$\begin{array}{rl}& i_i=\sigma \left({W_i^{(t)}}^{\top }\mathrm{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right)\\ & f_i=\sigma \left({W_f^{(t)}}^{\top }\mathrm{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right)\\ & o_i=\sigma \left({W_o^{(t)}}^{\top }\mathrm{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right)\\ & \tilde{C}=\tanh \left({W_c^{(t)}}^{\top }\mathrm{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right)\\ & C_i^{(t+1)}=f_i\odot C_i^{(t)}+i_i\odot \tilde{C}\\ & {\mu }_i^{(t+1)}=o_i\odot \tanh \left(C_i^{(t+1)}\right)\end{array}$$

Permutation invariant

自适应广度函数$\varphi (\cdot )$作用在邻居的一个线性转换，因此满足Theorem 1的排列不变性要求。
自适应深度函数$\phi (.)$作用在不同深度的层上，和任何一阶邻居的顺序无关。
因此，$\varphi \circ \phi$复合函数也是排列不变的。

3.3 Efficient Numerical Computation 高效的数值计算

• GeniePath算法能根据线性代数公式化表示，因此可以高效地在Intel MKL (Intel 2007) on CPUs or cuBLAS (Nvidia 2008) on GPUs上运行
• GeniePath算法的核心计算在公式（5）上
• GAT计算和存储复杂度需要$\mathcal{O}(N^2)$，而GeniePath只需$\mathcal{O}(|\mathcal{E}|)$

4 实验

4.1 数据集

Transductive setting

• Pubmed
• BlogCatalog，社交网络数据集，节点代表bloggers，边代表blogger之间的关系。这个数据集用于处理多标签分类问题。BlogCatalog 1数据集的节点没有显式特征，因此，用节点的第编码成one-hot的向量作为特征（10312维）。文中进一步在邻接矩阵A上通过SVD分解，建立了数据集128维的数据集BlogCatalog2。
• Alipay（来源于：2017. Poster: Neural network-based graph embedding for malicious accounts detection），是一种Account-Device Network类型的数据，用于检测支付宝在线无现金支付系统中的恶意账户。节点对应于由这些帐户登录的用户的帐户和设备。边对应于帐户和设备在一段时间内的登录关系。节点特征是将登录行为以小时计数和帐户配置文件。这个数据集中有两个类，恶意帐户和正常帐户。支付宝数据集在一周内随机采样。数据集由82,246个不相交子图组成。

Inductive setting

• PPI，蛋白质相互作用关系的数据集，由24个子图构成，每个子图对应于人体的一个组织。通过定位基因集、motif基因集和免疫标记提取节点特征。在基因论中，每个节点有121个类。每个节点可以有多个标签，从而导致一个多标签分类问题。文中使用GraphSAGE提供的预处理过的数据。训练用图20张，验证用图2张，测试用图2张。

4.2 实验设置

baselines

• MLP (multilayer perceptron)，只是用节点特征而不使用图的结构特征
• node2vec (Grover and Leskovec 2016)，基于查找embedding的方法不能处理多图问题（例如，PPI和支付宝数据集）
• Chebyshev (Defferrard, Bresson, and Vandergheynst 2016)，用切比雪夫多项式的T-th阶近似的普图卷积
• GCN (Kipf and Welling 2016)
  对称归一化版本（GCN）：$H^{(t+1)}=\sigma \left({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{H}^{(t)}{W}^{(t)}\right)$，只能用于transductive的任务；
  非对称版本（文中定义为GCN-mean）：$H^{(t+1)}=\sigma \left({\hat{D}}^{-1}\hat{A}{H}^{(t)}{W}^{(t)}\right)$ ， 可以处理inductive的任务
• GraphSAGE (Hamilton, Ying, and Leskovec 2017a)，有一组pooling操作和skip连接（残差连接）组成。文中用GraphSAGE∗代表不同的pooling策略中效果最好的
• Graph Attention Networks (GAT) (Veličković et al. 2017)，GAT类似于文中只有自适应广度函数的简化版本。有助于理解自适应广度和深度函数的实用性。

GeniePath∗表示文中GeniePath或GeniePath-lazy中效果最好的。实验中还发现，各种不同方法使用残差连接（跳跃连接）对堆叠多层卷积都是有益的。

Experimental Setups

• Tensorflow实现，使用Adam优化器
• 所有图卷积方法的embedding维度、学习率等超参数都相同
• node2vec：$p=q=1$
• 每个节点采样10条路径，长度为80
• 不同方法使用$l_2$正则化惩罚

Transductive setting

• 在这种条件下，使用整图训练，包括所有节点的所有边，所有节点的特征向量
• Pubmed数据集：两层卷积，隐藏单元数16
• BlogCatalog1和BlogCatalog2：3层卷积，隐藏单元数量128
• Alipay：7层卷积，隐藏单元数16

Inductive setting

• 在这种条件下，测试节点在训练过程中是不可观测的
• PPI数据集：3层卷积，隐藏单元数量256

4.3 Classification

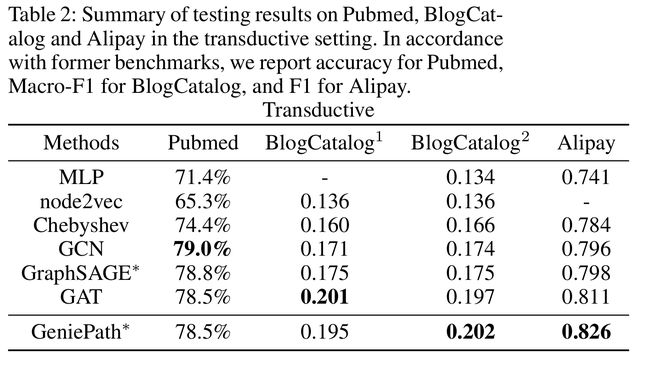
• 表2是transductive settings的对比
• Pubmed数据集只有60个标签可以用于训练
• 2 hidden convolutional layers时，GCN表现最好，当超过两层时，性能会降低
• 数据集太小限制了GeniePath的能力
• Alipay中的图比较稀疏，GeniePath在这种大图上性能很好，node2vec不能用于这种数据

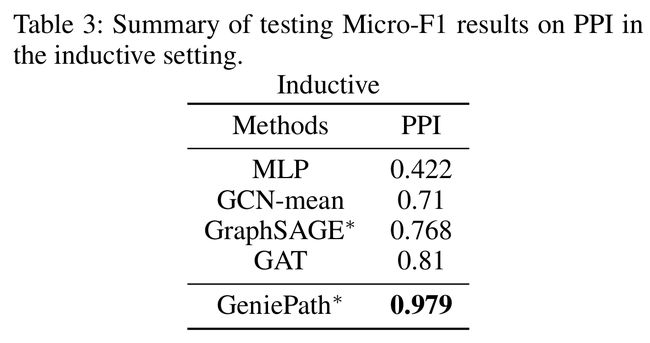
• 表3是inductive settings的对比
• GCN-mean在PPI数据集上的准确率可以达到0.71
• GAT只用了自适应广度函数，而GeniePath结合了自适应广度函数和自适应深度函数，图中GeniePath∗中的准确率比GAT高

• 表4展示了残差连接的作用
• GAT更依赖于残差结构，而GeniePath对残差连接不敏感

4.4 Depths of Propagation

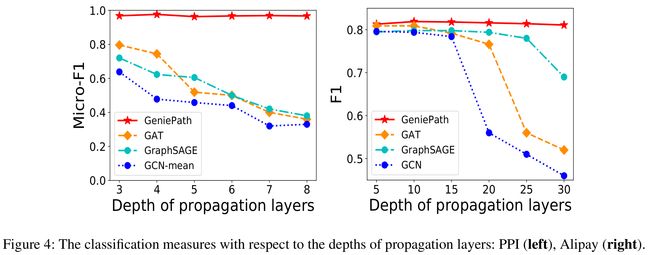
• 图4对比了传播层的深度对分类准确率的影响
• 层数加深，感受野变宽变深，GCN，GAT，GraphSAGE的分类准确率都会降低
• GeniePath能自适应的学习感知路径，随着层数增加，分类准确率并不会受到太大影响，效果remarkable

4.5 Qualitative Analysis

• 图5是关于一个通过GeniePath学到的采样节点的感知路径的定性分析
• 左图：图拉普拉斯同样程度地分配重要性给邻居节点，也就是说在路径很深的时候，每个邻居都是一样重要的
• 右图：GeniePath能够帮助选择非常重要的路径（红色）传播而忽略掉其他不重要的，最终的路径更稀疏。这种“邻居选择”的方式指导了感知路径的方向，并且提升了传播效率
• 图中用不同颜色的边来表示边$(i,j)$的重要性$w_{i,j}=\alpha \left(h_i,h_j\right)$：绿色（$w_{i,j}<0.1$），蓝色（$0.1\le w_{i,j}<0.2$），红色（$w_{i,j}\ge 0.2$）

5 小结

• 研究了图卷积网络寻找有意义的感受路径的问题
• 提出了能指导寻找感受路径，由自适应广度函数和自适应深度函数构成的自适应路径层
• 实验表明， 在大型数据上，GeniePath比当前state-of-the-art的方法效果都好，并且对叠加层的深度不敏感
• GeniePath的成功表明对不同节点选择合适的感受路径是很重要的
• 在研究邻居节点顺序很重要的temporal graphs上具有很大的挑战