树链剖分瞎入门
本文旨在让读者背代码
前言
在做题时,我们可能会遇到这样一类问题:
给定一棵 n n n 个结点的树和 m m m 次操作,操作有两种,一种是给定两个结点,让连接两个结点的路径上的所有点权值加上一个值,另一种是查询路径上所有点的权值和。 n ≤ 1 e 5 n\le 1e5 n≤1e5, m ≤ 2 e 5 m\le 2e5 m≤2e5。
如果是最后统一输出结点权值,用树上差分+ DFS \text{DFS} DFS 就能轻松水过,而对于在线查询,如果数据范围小的话暴力即可 AC \text{AC} AC,时间复杂度 O ( n m ) \text{O}(nm) O(nm),但是很明显,这个数据范围肯定不能这么写了。此时,就需要树链剖分出场了。
树链剖分
原理
树链剖分是根据轻重儿子,将一棵树剖成多条链,然后就可以用数据结构来维护这些链了,听着似乎还是有点像暴力,不过因为一条链有多个结点,所以可以优化时间复杂度。
至于轻重儿子的定义,请见下一块。
实现
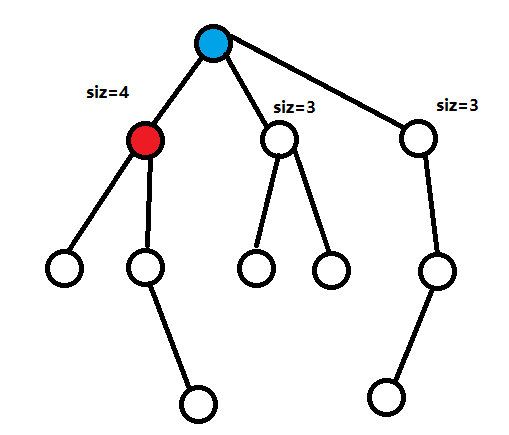
既然要把树剖成一堆链,那么我们就要有一种标准来剖这棵树,树链剖分的标准是什么呢?我们定义:一个结点的所有子树中,结点数最多的子树的根节点是这个结点的“重儿子”,比如下面这张图中,红点就是蓝点的重儿子。
递归进行这个过程,我们可以得到一堆的“重儿子”,将这些重儿子连起来,我们就会得到一根“重链”,最后对整棵树完成这个过程后,我们就将一棵树剖成了若干个“重链”。
剖完之后,还有一些点,它们则称为“轻儿子”,一些轻边连成的链则称为轻链。(然而这个并没有什么卵用)
此时我们已经剖完了树,我们就要考虑怎么维护这些链了。在说怎么维护之前,我们先把怎么剖用代码的方式表示出来。
对于树链剖分,我们需要维护以下的数组:
| 名称 | 含义 |
|---|---|
| s i z [ u ] siz[u] siz[u] | 以 u u u 为根的子树的结点个数 |
| s o n [ u ] son[u] son[u] | u u u 的重儿子的编号 |
| t o p [ u ] top[u] top[u] | u u u 所在链的深度最小的结点编号 |
| d e p [ u ] dep[u] dep[u] | u u u 的深度 |
| f a z [ u ] faz[u] faz[u] | u u u 的父亲的编号 |
| d f n [ u ] dfn[u] dfn[u] | u u u 的 DFS \text{DFS} DFS 序 |
| r k [ u ] rk[u] rk[u] | u u u 树中的编号 |
注:每个轻儿子的 t o p top top 就是它本身。
首先,因为我们在 DFS \text{DFS} DFS 时应该先往重儿子搜索,所以一个 DFS \text{DFS} DFS 肯定是不能完成任务,所以我们需要两个 DFS \text{DFS} DFS 函数。
这两个 DFS \text{DFS} DFS 函数分别完成什么呢?
Dfs1 \text{Dfs1} Dfs1:预处理 s i z siz siz, s o n son son, d e p dep dep, f a z faz faz 数组。
void Dfs1(int u)
{
siz[u]=1;
son[u]=0;
for(int i=fst[u];i;i=nxt[i])
{
int v=to[i];
if(v==faz[u]) continue;
dep[v]=dep[u]+1;
faz[v]=u;
Dfs1(v);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
Dfs2 \text{Dfs2} Dfs2:预处理 d f n dfn dfn, t o p top top, r k rk rk 数组。其中 r k rk rk 数组一般用不到,在大部分题目中可以省略。
void Dfs2(int u,int rt)
{
dfn[u]=++Index;
rk[Index]=u;
top[u]=rt;
if(son[u]) Dfs2(son[u],rt);
for(int i=fst[u];i;i=nxt[i])
{
int v=to[i];
if(v==faz[u] || v==son[u]) continue;
Dfs2(v,v);
}
}
注意点: Dfs1 \text{Dfs1} Dfs1 没有什么好注意的, Dfs2 \text{Dfs2} Dfs2 的时候记得先往重儿子搜,至于为什么?
维护链
DFS \text{DFS} DFS 序
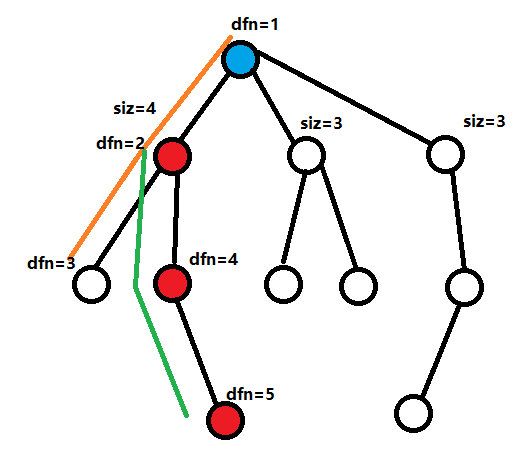
首先讲一下,为什么要先搜重儿子。因为我们要维护的是重链,而一条链的要求必须是连续的,而我们维护时使用数据结构,必然是要将它转换到数列上来做的,如何转换呢?最好的方法就是按照 DFS \text{DFS} DFS 序,此时如果不先搜重儿子的话,重链上的 DFS \text{DFS} DFS 序就可能会断掉,如下图(橙、绿线是 DFS \text{DFS} DFS 搜索顺序):
这条链的 DFS \text{DFS} DFS 序就断开了,此时就无法用数据结构去维护了。
如何维护
这一节很简单,没什么好讲的,因为要维护的是链,而且我们现在已经保证链上的 DFS \text{DFS} DFS 序连续了,所以我们直接取结点的 t o p top top 到它自己这一段进行修改或查询(即使用 DFS \text{DFS} DFS 序修改),然后再将当前结点跳到它 t o p top top 的 f a z faz faz 即可。为了防止一个结点无限往上跳,我们先选 t o p top top 比较深的那个结点进行修改/查询,再往上跳,就可以防止无限跳的情况了。而如果选的是浅的,而它又往上跳,则深度越来越浅,必然会无限跳,最终死循环。
最后,这两个结点一定会到一条链上,而且必然有一个点会是 LCA \text{LCA} LCA,我们最后进行一次操作即可。
至于为什么是跳到 t o p top top 的 f a z faz faz,因为 t o p top top 已经被修改/查询过了,跳到上一个结点防止重复操作。
修改:
void ModifyOnTree(int u,int v,int val)
{
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
Modify(1,1,n,dfn[top[u]],dfn[u],val);
u=faz[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
Modify(1,1,n,dfn[u],dfn[v],val);
}
查询(根据求和、求最小值、求最大值修改,仅给出求和):
int QueryOnTree(int u,int v)
{
int res=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
res+=Query(1,1,n,dfn[top[u]],dfn[u]);
u=faz[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
res+=Query(1,1,n,dfn[u],dfn[v]);
return res;
}
至于其中的 Modify \text{Modify} Modify 和 Query \text{Query} Query 函数,根据不同的需求和使用的数据结构的不同,应自行修改。
例题
P3384 【模板】树链剖分
链接
操作涉及区间加、区间和、子树加、子树和,区间的两种操作直接用线段树配合上面的模板可以轻松过去,而子树加和子树和这两个新操作呢?其实更简单。我们知道,一个子树的 DFS \text{DFS} DFS 序必然是连续的,所以我们直接对 d f n [ x ] dfn[x] dfn[x] 到 d f n [ x ] + s i z [ x ] − 1 dfn[x]+siz[x]-1 dfn[x]+siz[x]−1 这个序列进行区间加、区间和的操作即可,使用线段树即可无脑水过。
代码因为年代久远,码风太丑,不贴了。
P2590 [ZJOI2008]树的统计
链接
操作涉及单点修改、区间最大值、区间和,无脑水过。
#includeP3178 [HAOI2015]树上操作
链接
操作涉及单点加、子树加、区间和,依然无脑水过。
#includeP4315 月下“毛景树”
链接
操作涉及单点覆盖、区间覆盖、区间加、区间最大值,本来应该是无脑水过,但是因为要将边权转成点权,然后忽略掉 LCA \text{LCA} LCA,还是有点难度,具体解析见:题解 P4315 【月下“毛景树”】
#includeP4114 Qtree1
链接
和上一题一样,边权转点权,无脑操作即可。
#includeP1505 [国家集训队]旅游
链接
最后一道,来道毒瘤的,操作涉及单点修改,区间取相反数,区间和,区间最大值,区间最小值,其他的都简单,就是区间取相反数较难,我们在取相反时,将最大值和最小值交换,然后将和、最大值、最小值全部乘上 − 1 -1 −1 就行,码量较大,耐心码耐心调还是可以比较轻松的 A \text{A} A 掉的。
#include总结
无。
树链剖分是树上操作强大的工具,配合着数据结构对大部分操作有奇效,需要认真学习巩固。
FIN. \text{FIN.} FIN.