LeetCode精选好题(四)
文章目录
- 1、位1的个数
- 方法 1:循环和位移动
- 方法 2:位操作的小技巧
- 代码实现:
- 2、汉明距离
- 思路:
- 代码实现:
- 3、旋转数组
- 4、除自身以外数组的乘积
- 思路:
- 代码实现:
- 5、合并K个有序链表(困难)
- 思路:
- 代码实现:
- 6、数组中第K个最大元素
- 思路:
- 复杂度分析:
- 代码实现:
1、位1的个数
编写一个函数,输入是一个无符号整数,返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
方法 1:循环和位移动
这个方法比较直接。我们遍历数字的 32 位。如果某一位是 111 ,将计数器加一。
我们使用 位掩码 来检查数字的第 ithi^{th}ith 位。一开始,掩码 m=1m=1m=1 因为 111 的二进制表示是
0000 0000 0000 0000 0000 0000 0000 00010000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0001 0000 0000 0000 0000 0000 0000 0000 0001
显然,任何数字跟掩码 111 进行逻辑与运算,都可以让我们获得这个数字的最低位。检查下一位时,我们将掩码左移一位。
0000 0000 0000 0000 0000 0000 0000 00100000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0010 0000 0000 0000 0000 0000 0000 0000 0010
并重复此过程。
方法 2:位操作的小技巧
我们可以把前面的算法进行优化。我们不再检查数字的每一个位,而是不断把数字最后一个 111 反转,并把答案加一。当数字变成 000 的时候偶,我们就知道它没有 111 的位了,此时返回答案。
这里关键的想法是对于任意数字 nnn ,将 nnn 和 n−1n - 1n−1 做与运算,会把最后一个 111 的位变成 000 。为什么?考虑 nnn 和 n−1n - 1n−1 的二进制表示。
在二进制表示中,数字 nnn 中最低位的 111 总是对应 n−1n - 1n−1 中的 000 。因此,将 nnn 和 n−1n - 1n−1 与运算总是能把 nnn 中最低位的 111 变成 000 ,并保持其他位不变。
代码实现:
public int hammingWeight(int n) {
int sum = 0;
while (n != 0) {
sum++;
n &= (n - 1);
}
return sum;
}
2、汉明距离
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数 x 和 y,计算它们之间的汉明距离。
示例:
输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
思路:
异或,计数
我也不知道题解里讲的是啥,这样不好吗?
代码实现:
int hammingDistance(int x, int y) {
int z = x^y;
int count = 0;
while(z){
z&=(z-1);
count++;
}
return count;
}
3、旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
说明:
尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。 要求使用空间复杂度为 O(1) 的 原地 算法。
思路与代码:
奇技淫巧 – 原地旋转数组
4、除自身以外数组的乘积
给你一个长度为 n 的整数数组 nums,其中 n > 1,返回输出数组 output ,其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
示例:
输入: [1,2,3,4]
输出: [24,12,8,6]
提示:题目数据保证数组之中任意元素的全部前缀元素和后缀(甚至是整个数组)的乘积都在 32 位整数范围内。
说明: 请不要使用除法,且在 O(n) 时间复杂度内完成此题。
进阶:
你可以在常数空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组不被视为额外空间。)
思路:
左一遍,右一遍,得到两个乘积数组,再对号乘起来。
进阶:右一遍直接不要存数组里了,边循环边对号乘起来。
代码实现:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> ans(nums.size(),1);
int prods=1;
for(int i=0;i<nums.size()-1;i++){
ans[i+1]=ans[i]*nums[i];
}
for(int i=nums.size()-1;i>0;i--){
prods*=nums[i];
ans[i-1]*=prods;
}
return ans;
}
进阶版代码实现:
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
vector<int> answer(length);
// answer[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素, 所以 answer[0] = 1
answer[0] = 1;
for (int i = 1; i < length; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
// R 为右侧所有元素的乘积
// 刚开始右边没有元素,所以 R = 1
int R = 1;
for (int i = length - 1; i >= 0; i--) {
// 对于索引 i,左边的乘积为 answer[i],右边的乘积为 R
answer[i] = answer[i] * R;
// R 需要包含右边所有的乘积,所以计算下一个结果时需要将当前值乘到 R 上
R *= nums[i];
}
return answer;
}
};
5、合并K个有序链表(困难)
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6
思路:
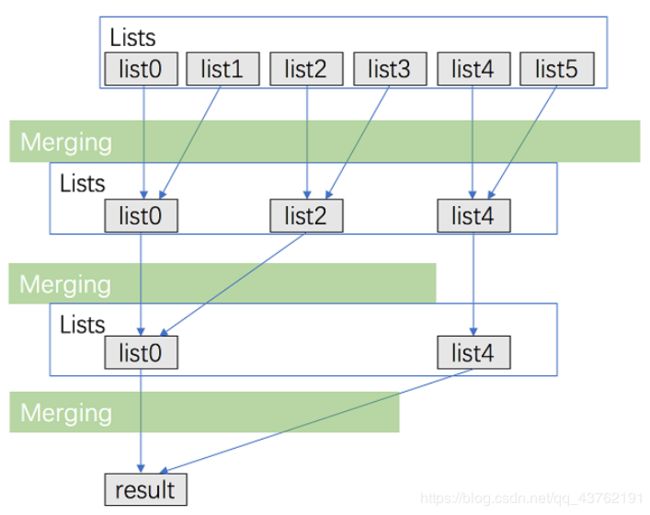
将 k 个链表配对并将同一对中的链表合并;
第一轮合并以后, k 个链表被合并成了 k\2个链表,平均长度为 2n\k,然后是 k\4个链表, k\8 个链表等等;
重复这一过程,直到我们得到了最终的有序链表。
代码实现:
class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* merge(vector <ListNode*> &lists, int l, int r) {
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
};
6、数组中第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
思路:
我们可以改进快速排序算法来解决这个问题:在分解的过程当中,我们会对子数组进行划分,如果划分得到的 q 正好就是我们需要的下标,就直接返回 a[q];否则,如果 q 比目标下标小,就递归右子区间,否则递归左子区间。这样就可以把原来递归两个区间变成只递归一个区间,提高了时间效率。这就是「快速选择」算法。
我们知道快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n的问题我们都划分成 1和 n−1,每次递归的时候又向 n−1的集合中递归,这种情况是最坏的,时间代价是O(n ^ 2)。我们可以引入随机化来加速这个过程,它的时间代价的期望是 O(n)
复杂度分析:
时间复杂度:O(n)。
空间复杂度:O(logn),递归使用栈空间的空间代价的期望为 O(logn)。
代码实现:
class Solution {
public:
int quickSelect(vector<int>& a, int l, int r, int index) {
int q = randomPartition(a, l, r);
if (q == index) {
return a[q];
} else {
return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
}
}
inline int randomPartition(vector<int>& a, int l, int r) {
int i = rand() % (r - l + 1) + l;
swap(a[i], a[r]);
return partition(a, l, r);
}
inline int partition(vector<int>& a, int l, int r) {
int x = a[r], i = l - 1;
for (int j = l; j < r; ++j) {
if (a[j] <= x) {
swap(a[++i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
int findKthLargest(vector<int>& nums, int k) {
srand(time(0));
return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
}
};