考研数学高等数学-函数

一、函数

1 函数

1.1 函数的定义

设x和y是两个变量(均在实数集R内取值)，D是一个给定的非空数集，如果对于每个数x∈D，按照某个对应法则f，变量y都有唯一确定的数值和它对应，则称变量y是变量x的函数，记作y=f(x)。其中D称为函数y=f(x)的定义域，x称为自变量，y称为因变量。函数值f(x)的全体所构成的集合称为函数f的值域。

1.2 函数的性质

1.2.1 有界性

设y=f(x)在区间I上有定义，如果存在正数M，对于任意x∈I，恒有|f(x)|≤M，则称y=f(x)在区间I上有界；否则称为无界。
如果存在实数M1，对于任意x∈I，恒有f(x)≤M1，则称y=f(x)在区间I上有上界；
如果存在实数M2，对于任意x∈I，恒有f(x)≥M2，则称y=f(x)在区间I上有下界；
y=f(x)在区间I上有界⟺既有上界又有下界。

1.2.2 单调性

设y=f(x)在区间I上有定义，如果∀x1，x2∈I，当x1f(x2))，则称y=f(x)在区间I上是单调增加(或单调减小)的。

1.2.3 周期性

设f(x)的定义域为D，如果存在一个不为零的常数T，使得对于任一x∈D，有x±T∈D且f(x±T)=f(x)，则f(x)称为周期函数，T称为f(x)的周期。通常把满足上式的最小正数T称为f(x)的周期。

1.2.4 奇偶性

设f(x)的定义域D关于原点对称，如果对于任一x∈D，恒有f(-x)=f(x)(或f(-x)=-f(x))，则称f(x)为偶函数(或奇函数)。偶函数的图形关于y轴对称，奇函数的图形关于原点对称。

1.3 复合函数

设y=f(u)，u=φ(x)，若φ(x)的值域与f(u)的定义域有非空交集，则由y=f(u)及u=φ(x)可复合而成复合函数y=f[φ(x)]，u称为中间变量。

1.4 反函数

设y=f(x)的定义域为D，值域为W。若∀y∈W，存在唯一确定的x∈D，满足y=f(x)，则得到的x是y的函数，记为x=φ(y)，称为y=f(x)的反函数，习惯成记为y=f-1(x)。

1.5 隐函数

设有关系式F(x,y)=0，若对∀x∈D，存在唯一确定的y满足F(x,y)=0与x相对应，由此确定的y与x的函数关系y=y(x)称为由方程F(x,y)=0所确定的隐函数。

2 基本初等函数及初等函数

2.1 基本初等函数

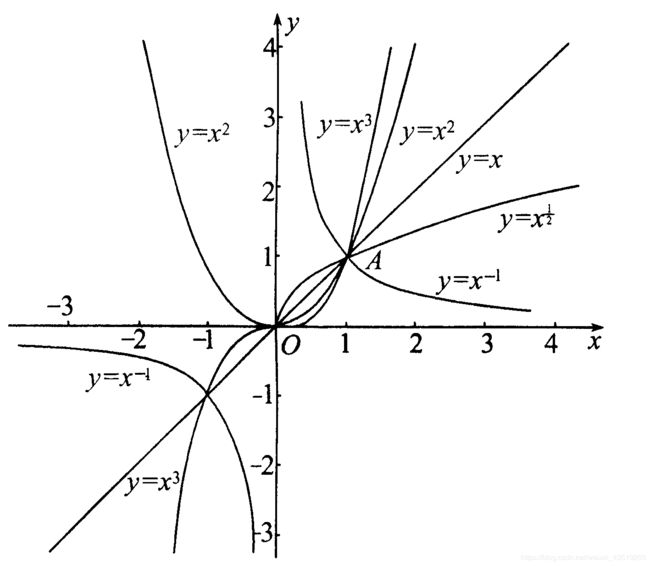
2.1.1 幂函数

$y=x^{\alpha },(\alpha \in N)$

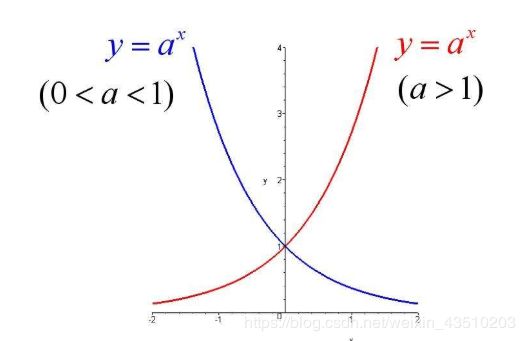
2.1.2 指数函数

$y=a^x,(a>0,a\ne 1)$

2.1.3 对数函数

$y={\log }_{a}x,(a>0,a\ne 1)$

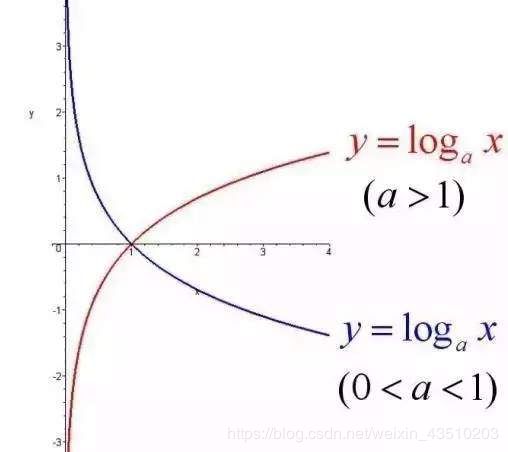
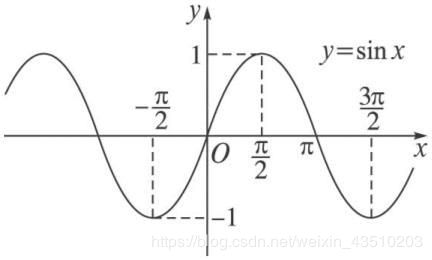
2.1.4 三角函数

• 正弦函数
  $y=\sin x，x\in (-\infty ,+\infty ),y\in [-1,1],T=2\pi$
  
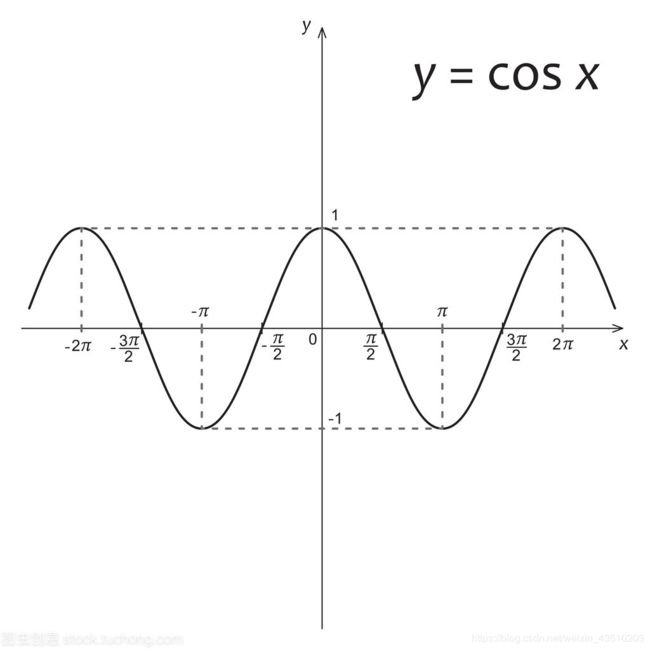
• 余弦函数
  $y=\cos x,x\in (-\infty ,+\infty ),y\in [-1,1],T=2\pi$
  
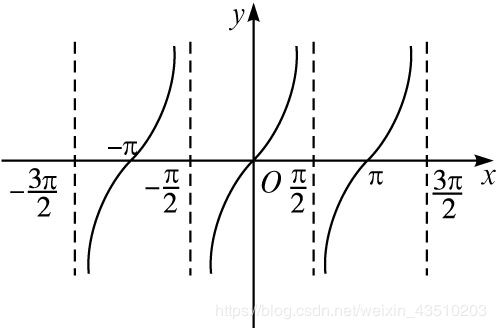
• 正切函数
  $y=\tan x,x\in \{x|x\ne K\pi \pm \frac{\pi }{2},K\in Z\},y\in (-\infty ,+\infty ),T=\pi$
  
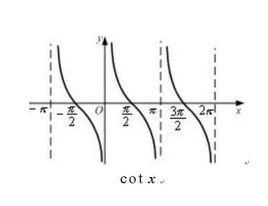
• 余切函数
  $y=\cot x,x\in \{x|x\ne K\pi ,K\in Z\},y\in (-\infty ,+\infty ),T=\pi$
  
• 正割函数
  $y=\sec x=\frac{1}{\cos x},x\in \{x|x\ne K\pi \pm \frac{\pi }{2},K\in Z\},y\in (-\infty ,1]\cup [1,+\infty ),T=2\pi$
  
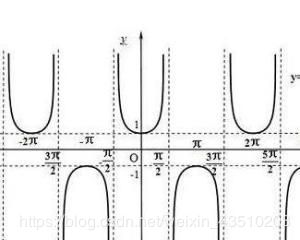
• 余割函数
  $y=\csc x=\frac{1}{\sin x},x\in \{x|x\ne K\pi ,K\in Z\},y\in (-\infty ,1]\cup [1,+\infty ),T=2\pi$
  

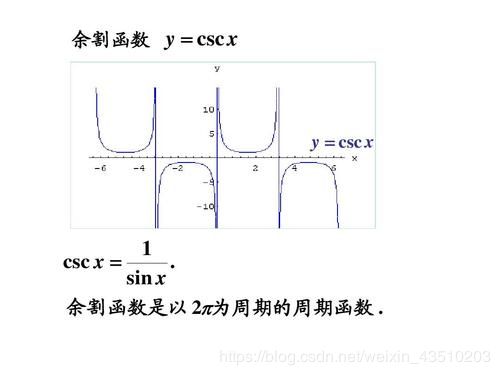
2.1.5 反三角函数

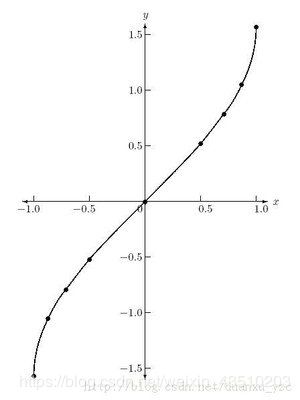
• 反正弦函数
  $y=\arcsin x,x\in [-1,1],y\in [-\frac{\pi }{2},\frac{\pi }{2}]$
  
• 反余弦函数
  $y=\arccos x,x\in [-1,1],y\in [0,\pi ]$
  
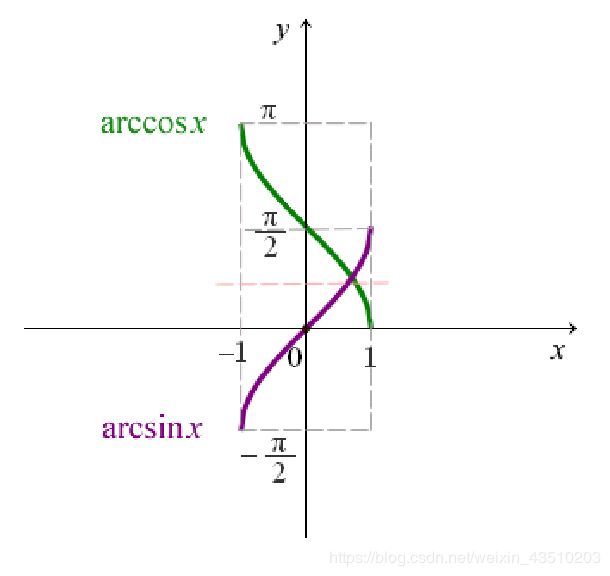
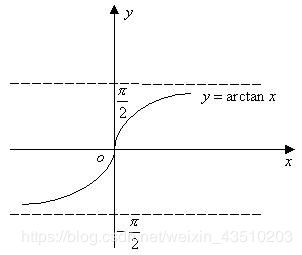
• 反正切函数
  $y=\arctan x,x\in (-\infty ,+\infty ),y\in (-\frac{\pi }{2},\frac{\pi }{2})$
  
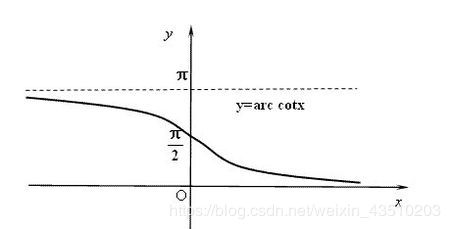
• 反余切函数
  $y=arccotx,x\in (-\infty ,+\infty ),y\in (0,\pi )$
  

2.2 初等函数

由常数和基本初等函数经过有限次四则运算和有限次的复合运算所构成并可用一个式子表示的函数称为初等函数。

3 常用函数

3.1 绝对值函数

$y=|x|=\{\begin{array}{r}x,当x\ge 0\\ -x,当x<0\end{array}$

3.2 符号函数

$y=sgnx=\{\begin{array}{r}1,当x>0\\ 0,当x=0\\ -1,当x<0\end{array}$

3.3 取整函数

$y=[x]$

3.4 狄利克雷函数

$y=D(x)=\{\begin{array}{r}1,当x是有理数时\\ 0,当x是无理数时\end{array}$

3.5 最值函数

$y=max\{f(x),g(x)\},y=min\{f(x),g(x)\}.$

3.6 变积分上限函数

设函数f(x)在区间[a,b]上连续，且x∈[a,b]，如果${\int }_a^{x}f(t)dt$的上限x在区间[a,b]上任意变动，则对于每一个取定的x值，定积分有一个对应值，所以它在[a,b]上定义了一个函数，记
$\Phi (x)={\int }_a^{x}f(t)dt$