【机器学习系列】之SVM核函数和SMO算法
作者:張張張張
github地址:https://github.com/zhanghekai
【转载请注明出处,谢谢!】
【机器学习系列】之SVM硬间隔和软间隔
【机器学习系列】之SVM核函数和SMO算法
【机器学习系列】之支持向量回归SVR
【机器学习系列】之sklearn实现SVM代码
一、SVM核函数
SVM基本型假设的是训练样本是线性可分的,即存在一个划分超平面能将训练样本正确分类。然而在现实任务中,原始样本空间内也许并不存在一个能正确划分两类样本的超平面,如下图所示的“异或”问题就不是线性可分的。

对于这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。如果原始空间是有限维,即特征数有限,那么一定存在一个高维特征空间使样本可分。
1.核函数的介绍
定义一个低维特征空间到高维特征空间的映射 ϕ \phi ϕ,令 ϕ ( x ) \phi(x) ϕ(x)表示将 x x x映射后的特征向量,将所有特征映射到一个更高的维度,让数据线性可分。此时,SVM的优化目标函数变成:
m i n ⎵ α 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) − ∑ i = 1 m α i s . t . ∑ i = 1 m α i y i = 0 0 ≤ α i ≤ C \underbrace{min}_{\alpha}\;\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_i y_j\phi(x_i)^T\phi(x_j)-\sum_{i=1}^{m}\alpha_i\\ s.t.\;\sum_{i=1}^{m}\alpha_iy_i=0\\ 0\leq\alpha_i\leq C α min21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj)−i=1∑mαis.t.i=1∑mαiyi=00≤αi≤C
由此可见,和线性可分SVM的优化目标函数的区别仅仅是将内积 x i T x j x_i^T x_j xiTxj替换为 ϕ ( x i ) T ϕ ( x j ) \phi(x_i)^T\phi(x_j) ϕ(xi)Tϕ(xj)。
若低维特征过多,映射到高维的维度特征是程几何暴增的,解决低维特征过多的问题,于是就引出了“核函数”。
“核函数”的定义: 假设 χ \chi χ为低维输入空间, κ ( ⋅ , ⋅ ) \kappa(\cdot,\cdot) κ(⋅,⋅)是定义在 χ × χ \chi\times\chi χ×χ上的对称函数,则 κ \kappa κ是核函数的充要条件是当且仅当对于任意数据 D = { x 1 , x 2 , ⋯ , x m } D=\{x_1,x_2,\cdots,x_m\} D={x1,x2,⋯,xm},“核矩阵(kernel matrix)” k k k 总是半正定的:
其中: κ ( x i , x j ) = ϕ ( x i ) T ϕ ( x j ) \kappa(x_i,x_j)=\phi(x_i)^T\phi(x_j) κ(xi,xj)=ϕ(xi)Tϕ(xj)
那么我们就称 κ ( x i , x j ) \kappa(x_i,x_j) κ(xi,xj)为核函数。上述定义表明:只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用。 κ ( x i , x j ) \kappa(x_i,x_j) κ(xi,xj)的计算是在低维特征空间来计算的,它避免了在高维空间计算内积的恐怖计算量。
线性不可分核函数的引入过程: 我们遇到线性不可分的样例时,常用做法是把样例特征映射到高维空间中去,但是遇到线性不可分的样例,若一律映射到高维空间,那么这个维度大小是会高到令人恐怖的。此时,核函数就体现出它的价值了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,核函数是在低维空间上进行计算,而将实质上的分类效果(利用内积)表现在了高维上,这样避免了直接在高维空间中的复杂计算,真正解决了SVM线性不可分的问题。
2.几种常用的核函数
- 若 κ 1 \kappa_1 κ1和 κ 2 \kappa_2 κ2为核函数,则对于任意正数 γ 1 、 γ 2 \gamma_1、\gamma_2 γ1、γ2,其线性组合
γ 1 κ 1 + γ 2 κ 2 \gamma_1\kappa_1+\gamma_2\kappa_2 γ1κ1+γ2κ2
也是核函数。 - 若 κ 1 \kappa_1 κ1和 κ 2 \kappa_2 κ2为核函数,则核函数的直积
κ 1 ⨂ κ 2 ( x , z ) = κ 1 ( x , z ) κ 2 ( x , z ) \kappa_1\bigotimes\kappa_2(x,z)=\kappa_1(x,z)\kappa_2(x,z) κ1⨂κ2(x,z)=κ1(x,z)κ2(x,z)
也是核函数。 - 若 κ 1 \kappa_1 κ1为核函数,则对于任意函数 g ( x ) g(x) g(x),
κ ( x , z ) = g ( x ) κ 1 ( x , z ) g ( z ) \kappa(x,z)=g(x)\kappa_1(x,z)g(z) κ(x,z)=g(x)κ1(x,z)g(z)
也是核函数。
3.分类SVM算法流程
引入核函数后,SVM算法才算是比较完整了,现在对分类SVM的算法过程做一个总结,不再区分是否线性可分。

二、SMO算法
首先回顾下SVM的优化目标函数,SMO算法要求解如下凸二次规划的对偶问题:
m i n ⎵ α 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j κ ( x i , x j ) − ∑ i = 1 m α i s . t . ∑ i = 1 m α i y i = 0 0 ≤ α i ≤ C \underbrace{min}_{\alpha}\;\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_i y_j\kappa(x_i,x_j)-\sum_{i=1}^{m}\alpha_i\\ s.t.\;\sum_{i=1}^{m}\alpha_iy_i=0\\ 0\leq\alpha_i\leq C α min21i=1∑mj=1∑mαiαjyiyjκ(xi,xj)−i=1∑mαis.t.i=1∑mαiyi=00≤αi≤C
其应满足如下KKT条件:
{ α i ≥ 0 , μ i ≥ 0 , y i ( w T x i + b ) − 1 + ξ i ≥ 0 , α i ( y i ( w T x i + b ) − 1 + ξ i ) = 0 ξ i ≥ 0 , μ i ξ i = 0 \begin{cases}\alpha_i\geq0, \qquad \mu_i \geq0,\\[2ex] y_i(w^Tx_i+b)-1+\xi_i \geq 0,\\[2ex] \alpha_i(y_i(w^Tx_i+b)-1+\xi_i)=0\\[2ex] \xi_i\geq0,\quad \mu_i\xi_i=0\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧αi≥0,μi≥0,yi(wTxi+b)−1+ξi≥0,αi(yi(wTxi+b)−1+ξi)=0ξi≥0,μiξi=0
SMO是一种启发式算法,其基本思路是: 它每次只优化两个变量,将其它的变量都视为常数。由于 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m}\alpha_iy_i = 0 ∑i=1mαiyi=0,假如将 α 3 , α 4 , ⋯ , α m \alpha_3,\alpha_4,\cdots,\alpha_m α3,α4,⋯,αm固定,那么 α 1 、 α 2 \alpha_1、\alpha_2 α1、α2之间的关系也确定了,这样SMO算法将一个复杂的优化算法转化为一个比较简单的两变量优化问题,这样目标优化函数变为:
m i n ⎵ α 1 , α 2 1 2 κ 11 α 1 2 + 1 2 κ 22 α 2 2 + y 1 y 2 κ 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 ∑ i = 3 m y i α i κ i 1 + y 2 α 2 ∑ i = 3 m y i α i κ i 2 ( 1 ) s . t . α 1 y 1 + α 2 y 2 = − ∑ i = 3 m y i α i 0 ≤ α i ≤ C i = 1 , 2 \underbrace{min}_{\alpha_1,\alpha_2}\;\frac{1}{2}\kappa_{11}\alpha_1^2+\frac{1}{2}\kappa_{22}\alpha_2^2+y_1y_2\kappa_{12}\alpha_1\alpha_2-(\alpha_1+\alpha_2)+y_1\alpha_1\sum_{i=3}^{m}y_i\alpha_i\kappa_{i1}+y_2\alpha_2\sum_{i=3}^{m}y_i\alpha_i\kappa_{i2}\qquad\qquad(1)\\ s.t.\quad \alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^{m}y_i\alpha_i\\ 0\leq\alpha_i\leq C\quad i=1,2 α1,α2 min21κ11α12+21κ22α22+y1y2κ12α1α2−(α1+α2)+y1α1i=3∑myiαiκi1+y2α2i=3∑myiαiκi2(1)s.t.α1y1+α2y2=−i=3∑myiαi0≤αi≤Ci=1,2
注释:
- 由于 y y y只能取 + 1 +1 +1或 − 1 -1 −1,所以 y i 2 y_i^2 yi2总为1;
- 上式省略了不含 α 1 、 α 2 \alpha_1、\alpha_2 α1、α2的常数项。
这样,在参数初始化后,SMO不断执行如下两个步骤直至收敛:
- 选取一对需要更新的变量 α i \alpha_i αi和 α j \alpha_j αj
- 固定 α i \alpha_i αi和 α j \alpha_j αj以外的参数,求解式(1)获得更新后的 α i \alpha_i αi和 α j \alpha_j αj
SMO伪代码大致如下
创建一个 alpha 向量并将其初始化为0向量
当迭代次数小于最大迭代次数时(外循环)
\qquad 对数据集中的每个数据向量(内循环):
\qquad\qquad 如果该数据向量可以被优化
\qquad\qquad\qquad 随机选择另外一个数据向量
\qquad\qquad\qquad 同时优化这两个向量
\qquad\qquad\qquad 如果两个向量都不能被优化,退出内循环
\qquad 如果所有向量都没被优化,增加迭代数目,继续下一次循环
1.SMO算法目标函数的优化
为了求解上面含有这两个变量的目标优化问题,我们首先分析约束条件,所有的 α 1 、 α 2 \alpha_1、\alpha_2 α1、α2都要满足约束条件,然后在约束条件下求最小值。根据上面的约束条件 α 1 y 1 + α 2 y 2 = k , 0 ≤ α i ≤ C i = 1 , 2 \alpha_1y_1+\alpha_2y_2=k,\quad0\leq\alpha_i\leq C\quad i=1,2 α1y1+α2y2=k,0≤αi≤Ci=1,2 ,又由于 y 1 , y 2 y_1,y_2 y1,y2均只能取值 1 1 1或者 − 1 -1 −1, 这样 α 1 , α 2 \alpha_1,\alpha_2 α1,α2在 [ 0 , C ] [0,C] [0,C]和 [ 0 , C ] [0,C] [0,C]形成的盒子里面,并且两者的关系直线的斜率只能为 1 1 1或者 − 1 -1 −1,也就是说 的关系直线平行于 [ 0 , C ] [0,C] [0,C]和 [ 0 , C ] [0,C] [0,C]形成的盒子的对角线。
由于 α 1 , α 2 \alpha_1,\alpha_2 α1,α2的关系被限制在盒子里的一条线段上,所以两变量的优化问题实际上仅仅是一个变量的优化问题。不妨我们假设最终是 α 2 \alpha_2 α2的优化问题。由于我们采用的是启发式的迭代法,假设我们上一轮迭代得到的解是 α 1 o l d , α 2 o l d \alpha_1^{old},\alpha_2^{old} α1old,α2old,假设沿着约束方向 α 2 \alpha_2 α2未经剪辑的解是 α 2 e w , u n c \alpha_2^{ew,unc} α2ew,unc(即:未考虑不等式约束 α \alpha α的取值范围 [ 0 , C ] [0,C] [0,C]的最优解),本轮迭代完成后的解为 α 1 n e w , α 2 n e w \alpha_1^{new},\alpha_2^{new} α1new,α2new(即:考虑不等式约束 α \alpha α的取值范围的最优解)。
由于 α 2 n e w \alpha_2^{new} α2new必须满足上图中的线段约束。假设 L L L和 H H H分别是上图中 α 2 n e w \alpha_2^{new} α2new所在的线段的边界。那么很显然有:
L ≤ α 2 n e w ≤ H L\leq\alpha_2^{new}\leq H L≤α2new≤H
初中数学知识: 我们把函数f(x)左移一个单位得到的函数就是f(x+1) 同样我们面对一个f(x+1)的函数 他的图像就是f(x)左移一个单位,即:“左加右减”原则。
- 当 y 1 y_1 y1不等于 y 2 y_2 y2时:
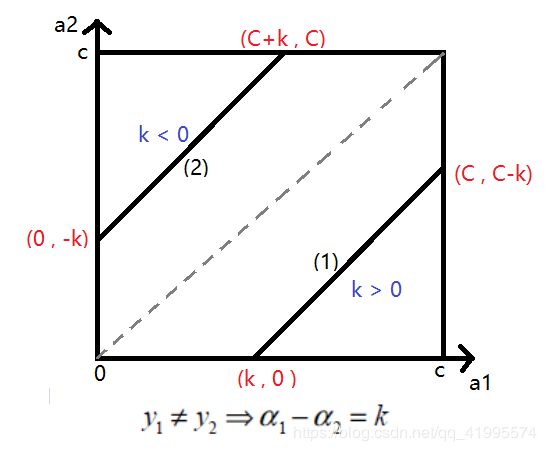
- 当 y 1 = 1 , y 2 = − 1 y_1=1,y_2=-1 y1=1,y2=−1时:有 α 1 − α 2 = k \alpha_1-\alpha_2=k α1−α2=k,此时 k > 0 k >0 k>0,如图中线段(1)所示。 α 2 \alpha_2 α2的取值范围为 α 2 ∈ ( 0 , C + α 2 − α 1 ) \alpha_2\in(0,C+\alpha_2-\alpha_1) α2∈(0,C+α2−α1)。当线段(1)移动到虚线上半部分后,此时情况为 y 1 = − 1 , y 2 = 1 y_1=-1,y_2=1 y1=−1,y2=1
- 当 y 1 = − 1 , y 2 = 1 y_1=-1,y_2=1 y1=−1,y2=1时:有 α 1 − α 2 = k \alpha_1-\alpha_2=k α1−α2=k,此时 k < 0 k<0 k<0,如图中线段(2)所示。 α 2 \alpha_2 α2的取值范围为 α 2 ∈ ( α 2 − α 1 , C ) \alpha_2\in(\alpha_2-\alpha_1,C) α2∈(α2−α1,C)。
- 此时 α 2 \alpha_2 α2的取值范围为: L = m a x ( 0 , α 2 o l d − α 1 o l d ) L=max(0,\alpha_2^{old}-\alpha_1^{old}) L=max(0,α2old−α1old); H = m i n ( C + α 2 o l d − α 1 o l d , C ) H=min(C+\alpha_2^{old}-\alpha_1^{old},C) H=min(C+α2old−α1old,C)
- 当 y 1 y_1 y1等于 y 2 y_2 y2时:
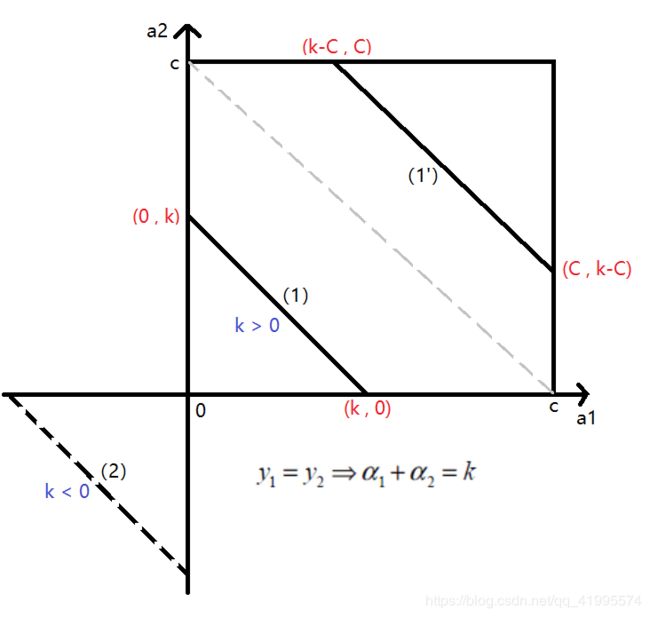
- 当 y 1 = y 2 = 1 y_1=y_2=1 y1=y2=1时:有 α 1 + α 2 = k \alpha_1+\alpha_2=k α1+α2=k,此时 k > 0 k>0 k>0,如图中线段(1)所示。此时 α 2 \alpha_2 α2的取值范围为 α 2 ∈ ( 0 , α 1 + α 2 ) \alpha_2\in(0,\alpha_1+\alpha_2) α2∈(0,α1+α2);当线段(1)移动到虚线上半部分后,如图中线段(1’),此时 α 2 \alpha_2 α2的取值范围为 α 2 ∈ ( α 1 + α 2 − C , C ) \alpha_2\in(\alpha_1+\alpha_2-C,C) α2∈(α1+α2−C,C)。
- 当 y 1 = y 2 = − 1 y_1=y_2=-1 y1=y2=−1时:有 α 1 + α 2 = k \alpha_1+\alpha_2=k α1+α2=k,此时 k < 0 k<0 k<0,如图中线段(2)所示。由于此线段并没有与 [ 0 , C ] [0,C] [0,C]和 [ 0 , C ] [0,C] [0,C]形成的盒子相交,所以不符合要求,在这种情况下 α 2 \alpha_2 α2没有极值。
- 此时 α 2 \alpha_2 α2的取值范围为: L = m a x ( 0 , α 1 o l d + α 2 o l d − C ) L=max(0,\alpha_1^{old}+\alpha_2^{old}-C) L=max(0,α1old+α2old−C); H = m i n ( α 1 o l d + α 2 o l d , C ) H=min(\alpha_1^{old}+\alpha_2^{old},C) H=min(α1old+α2old,C)
注释:
- 以上线段图像均可根据“左加右减”原则得到。
- L L L和 H H H指的是取二者中的最大/最小值,而不是范围。
- L L L取 m a x max max是因为 α 2 n e w \alpha_2^{new} α2new要比最小值中最大的那个值大; H H H取 m i n min min是因为 α 2 n e w \alpha_2^{new} α2new要比最大值中最小的那个值小,这样才能确保 α 2 n e w \alpha_2^{new} α2new完全在 L L L和 H H H之间
综上所述: 假如通过求导得到 α 2 n e w , u n c \alpha_2^{new,unc} α2new,unc,则最终的 α 2 n e w \alpha_2^{new} α2new应该为:
α 2 n e w = { H α 2 n e w , u n c > H α 2 n e w , u n c L ≤ α 2 n e w , u n c ≤ H L α 2 n e w , u n c < L \alpha_2^{new}=\begin{cases}H\qquad\qquad\alpha_2^{new,unc}>H\\ \alpha_2^{new,unc}\quad\;\; L\leq\alpha_2^{new,unc}\leq H\\ L\qquad\qquad\;\alpha_2^{new,unc}<L\end{cases} α2new=⎩⎪⎨⎪⎧Hα2new,unc>Hα2new,uncL≤α2new,unc≤HLα2new,unc<L
2. α 2 n e w , u n c 的 求 解 \;\;\alpha_2^{new,unc}的求解 α2new,unc的求解
令:
g ( x ) = w ∗ ⋅ ϕ ( x ) + b = ∑ j = 1 m α j ∗ y j κ ( x , x j ) + b ∗ E i = g ( x i ) − y i = ∑ j = 1 m α j ∗ y j κ ( x i , x j ) + b − y i v i = ∑ j = 3 m y j α j κ ( x i , x j ) = g ( x i ) − ∑ j = 1 2 y j α j κ ( x i , x j ) − b g(x)=w^*\cdot \phi(x)+b=\sum_{j=1}^{m}\alpha_j^*y_j\kappa(x,x_j)+b^* \\ E_i=g(x_i)-y_i=\sum_{j=1}^{m}\alpha_j^*y_j\kappa(x_i,x_j)+b-y_i \\v_i=\sum_{j=3}^{m}y_j\alpha_j\kappa(x_i,x_j)=g(x_i)-\sum_{j=1}^{2}y_j\alpha_j\kappa(x_i,x_j)-b g(x)=w∗⋅ϕ(x)+b=j=1∑mαj∗yjκ(x,xj)+b∗Ei=g(xi)−yi=j=1∑mαj∗yjκ(xi,xj)+b−yivi=j=3∑myjαjκ(xi,xj)=g(xi)−j=1∑2yjαjκ(xi,xj)−b
这样优化目标函数,即公式(1)进一步化简为:
W ( α 1 , α 2 ) = 1 2 κ 11 α 1 2 + 1 2 κ 22 α 2 2 + y 1 y 2 κ 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 v 1 + y 2 α 2 v 2 ( 2 ) W(\alpha_1,\alpha_2)=\frac{1}{2}\kappa_{11}\alpha_1^2+\frac{1}{2}\kappa_{22}\alpha_2^2+y_1y_2\kappa_{12}\alpha_1\alpha_2-(\alpha_1+\alpha_2)+y_1\alpha_1v_1+y_2\alpha_2v_2\qquad\qquad(2) W(α1,α2)=21κ11α12+21κ22α22+y1y2κ12α1α2−(α1+α2)+y1α1v1+y2α2v2(2)
由于 α 1 y 1 + α 2 y 2 = ζ \alpha_1y_1+\alpha_2y_2=\zeta α1y1+α2y2=ζ,并且 y i 2 = 1 y_i^2=1 yi2=1,可以得到 α 1 \alpha_1 α1用 α 2 \alpha_2 α2表达的式子为:
α 1 = y 1 ( ζ − α 2 y 2 ) ( 3 ) \alpha_1=y_1(\zeta-\alpha_2y_2)\qquad\qquad(3) α1=y1(ζ−α2y2)(3)
将式(3)带入到式(2)中,就可以消除 α 1 \alpha_1 α1,得到仅仅包含 α 2 \alpha_2 α2的式子:
W ( α 2 ) = 1 2 κ 11 ( ζ − α 2 y 2 ) 2 + 1 2 κ 22 α 2 2 + y 2 κ 12 ( ζ − α 2 y 2 ) α 2 − ( ζ − α 2 y 2 ) y 1 − α 2 + ( ζ − α 2 y 2 ) v 1 + y 2 α 2 v 2 ( 4 ) W(\alpha_2)=\frac{1}{2}\kappa_{11}(\zeta-\alpha_2y_2)^2+\frac{1}{2}\kappa_{22}\alpha_2^2+y_2\kappa_{12}(\zeta-\alpha_2y_2)\alpha_2-(\zeta-\alpha_2y_2)y_1-\alpha_2+(\zeta-\alpha_2y_2)v_1+y_2\alpha_2v_2\qquad\qquad(4) W(α2)=21κ11(ζ−α2y2)2+21κ22α22+y2κ12(ζ−α2y2)α2−(ζ−α2y2)y1−α2+(ζ−α2y2)v1+y2α2v2(4)
通过对式(4)求偏导数来得到 α 2 n e w , u n c \alpha_2^{new,unc} α2new,unc:
∂ W ∂ α 2 = κ 11 α 2 + κ 22 α 2 − 2 κ 12 α 2 − κ 11 ζ y 2 + κ 12 ζ y 2 + y 1 y 2 − 1 − v 1 y 2 + y 2 v 2 = 0 ( 5 ) \frac{\partial W}{\partial\alpha_2}=\kappa_{11}\alpha_2+\kappa_{22}\alpha_2-2\kappa_{12}\alpha_2-\kappa_{11}\zeta y_2+\kappa_{12}\zeta y_2+y_1y_2-1-v_1y_2+y_2v_2=0\qquad\qquad(5) ∂α2∂W=κ11α2+κ22α2−2κ12α2−κ11ζy2+κ12ζy2+y1y2−1−v1y2+y2v2=0(5)
整理上式(5),得:
( κ 11 + κ 22 − 2 κ 12 ) α 2 = y 2 ( y 2 − y 1 + ζ κ 11 − ζ κ 12 + v 1 − v 2 ) = y 2 ( y 2 − y 1 + ζ κ 11 − ζ κ 12 + ( g ( x 1 ) − ∑ j = 1 2 y j α j κ 1 j − b ) − ( g ( x 2 ) − ∑ j = 1 2 y j α j κ 2 j − b ) ) ( 6 ) (\kappa_{11}+\kappa_{22}-2\kappa_{12})\alpha_2=y_2(y_2-y_1+\zeta\kappa_{11}-\zeta\kappa_{12}+v_1-v_2)\\ =y_2(y_2-y_1+\zeta\kappa_{11}-\zeta\kappa_{12}+(g(x_1)-\sum_{j=1}^{2}y_j\alpha_j\kappa_{1j}-b)-(g(x_2)-\sum_{j=1}^{2}y_j\alpha_j\kappa_{2j}-b))\qquad\qquad(6) (κ11+κ22−2κ12)α2=y2(y2−y1+ζκ11−ζκ12+v1−v2)=y2(y2−y1+ζκ11−ζκ12+(g(x1)−j=1∑2yjαjκ1j−b)−(g(x2)−j=1∑2yjαjκ2j−b))(6)
将 ζ = α 1 y 1 + α 2 y 2 \zeta=\alpha_1y_1+\alpha_2y_2 ζ=α1y1+α2y2带入上式(6)中,得:
( κ 11 + κ 22 − 2 κ 12 ) α 2 n e w , u n c = y 2 ( ( κ 11 + κ 22 − 2 κ 12 ) α 2 o l d y 2 + y 2 − y 1 + g ( x 1 ) − g ( x 2 ) ) = ( κ 11 + κ 22 − 2 κ 12 ) α 2 o l d + y 2 ( E 1 − E 2 ) (\kappa_{11}+\kappa_{22}-2\kappa_{12})\alpha_2^{new,unc}=y_2((\kappa_{11}+\kappa_{22}-2\kappa_{12})\alpha_2^{old}y_2+y_2-y_1+g(x_1)-g(x_2))\\ =(\kappa_{11}+\kappa_{22}-2\kappa_{12})\alpha_2^{old}+y_2(E_1-E_2) (κ11+κ22−2κ12)α2new,unc=y2((κ11+κ22−2κ12)α2oldy2+y2−y1+g(x1)−g(x2))=(κ11+κ22−2κ12)α2old+y2(E1−E2)
最终得到了 α 2 n e w , u n c \alpha_2^{new,unc} α2new,unc的表达式:
α 2 n e w , u n c = α 2 o l d + y 2 ( E 1 − E 2 ) κ 11 + κ 22 − 2 κ 12 \alpha_2^{new,unc}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\kappa_{11}+\kappa_{22-2\kappa_{12}}} α2new,unc=α2old+κ11+κ22−2κ12y2(E1−E2)
利用上面讲到的 α 2 n e w , u n c \alpha_2^{new,unc} α2new,unc和 α 2 n e w \alpha_2^{new} α2new的关系式,就可以得到新的 α 2 n e w \alpha_2^{new} α2new了,利用 α 2 n e w \alpha_2^{new} α2new和 α 1 n e w \alpha_1^{new} α1new的线性关系,就可以得到新的 α 1 n e w \alpha_1^{new} α1new。
3.SMO算法两个变量的选择
3.1 第一个变量的选择
SMO算法称选择第一个变量为外层循环,这个变量需要选择在训练集中违反KKT条件最严重的样本点。直观来看,KKT条件违背的程度越大,则变量更新后可能导致的目标函数值增幅越大。于是,SMO先选取违背KKT调价程度最大的变量。
一般来说,首先选择违反 0 < α j ∗ < C ⟹ y i g ( x i ) = 1 0<\alpha_j^*<C\implies y_ig(x_i)=1 0<αj∗<C⟹yig(xi)=1这个条件的点。如果这些支持向量都满足KKT条件,再选择违反 α i ∗ = 0 ⟹ y i g ( x i ) ≥ 1 \alpha_i^*=0\implies y_ig(x_i)\geq 1 αi∗=0⟹yig(xi)≥1和 α i ∗ = C ⟹ y i g ( x i ) ≤ 1 \alpha_i^*=C\implies y_ig(x_i)\leq 1 αi∗=C⟹yig(xi)≤1的点。
3.2 第二个变量的选择
SMO算法称选择第二个变量为内层循环,第二个变量应选择一个使目标函数值增长最快的变量,即:让 ∣ E 1 − E 2 ∣ |E_1-E_2| ∣E1−E2∣有足够大的变化。由于 α 1 \alpha_1 α1定了的时候, E 1 E_1 E1也确定了,所以想要 ∣ E 1 − E 2 ∣ |E_1-E_2| ∣E1−E2∣最大,只需要在 E 1 E_1 E1为正时,选择最小的 E i E_i Ei作为 E 2 E_2 E2,在 E 1 E_1 E1为负时,选择最大的 E i E_i Ei作为 E 2 E_2 E2,可以将所有的 E i E_i Ei保存下来加快迭代。
如果内存循环找到的点不能让目标函数有足够的下降, 可以采用遍历支持向量点来做 α 2 \alpha_2 α2 ,直到目标函数有足够的下降, 如果所有的支持向量做 α 2 \alpha_2 α2都不能让目标函数有足够的下降,可以跳出内层循环,重新选择 α 1 \alpha_1 α1。
两个变量选择的总结: 这样的两个变量有很大的差别,与对两个相似的变量进行更新相比,对它们进行更新会带给目标函数值更大的变化。
4.计算阈值 b b b和差值 E i E_i Ei
在每次完成两个变量的优化之后,需要重新计算阈值 b b b
-
当 0 < α 1 n e w < C 0<\alpha_1^{new}<C 0<α1new<C时, 由 y i ( w i T + b ) = 1 y_i(w^T_i+b)=1 yi(wiT+b)=1知:
y 1 − ∑ i = 1 m α i y i κ i 1 − b 1 = 0 y_1-\sum_{i=1}^{m}\alpha_iy_i\kappa_{i1}-b_1=0 y1−i=1∑mαiyiκi1−b1=0新的 b 1 n e w 为 : b_1^{new}为: b1new为:
b 1 n e w = y 1 − ∑ i = 3 m α i y i κ i 1 − α 1 n e w y 1 κ 11 − α 2 n e w y 2 κ 21 ( 7 ) b_1^{new}=y_1-\sum_{i=3}^{m}\alpha_iy_i\kappa_{i1}-\alpha_1^{new}y_1\kappa_{11}-\alpha_2^{new}y_2\kappa_{21}\qquad\qquad(7) b1new=y1−i=3∑mαiyiκi1−α1newy1κ11−α2newy2κ21(7)计算出 E 1 E_1 E1为:
E 1 = g ( x 1 ) − y 1 = ∑ i = 3 m α i y i κ i 1 + α 1 o l d y 1 κ 11 + α 2 o l d y 2 κ 21 + b o l d − y 1 E_1=g(x_1)-y_1=\sum_{i=3}^{m}\alpha_iy_i\kappa_{i1}+\alpha_1^{old}y_1\kappa_{11}+\alpha_2^{old}y_2\kappa_{21}+b^{old}-y_1 E1=g(x1)−y1=i=3∑mαiyiκi1+α1oldy1κ11+α2oldy2κ21+bold−y1可以看到上述两式都有 y 1 − ∑ i = 3 m α i y i κ i 1 y_1-\sum_{i=3}^{m}\alpha_iy_i\kappa_{i1} y1−∑i=3mαiyiκi1,因此可以将 b 1 n e w b_1^{new} b1new用 E 1 E_1 E1表示:
b 1 n e w = − E 1 − y 1 κ 11 ( α 1 n e w − α 1 o l d ) − y 2 κ 21 ( α 2 n e w − α 2 o l d ) + b o l d ( 8 ) b_1^{new}=-E_1-y_1\kappa_{11}(\alpha_1^{new}-\alpha_1^{old})-y_2\kappa_{21}(\alpha_2^{new}-\alpha_2^{old})+b^{old}\qquad\qquad(8) b1new=−E1−y1κ11(α1new−α1old)−y2κ21(α2new−α2old)+bold(8)注释: 其实用公式(7)即可求出 b 1 n e w b_1^{new} b1new,但 E 1 E_1 E1是我们已知的值,为了避免冗余计算,所以用带有 E i E_i Ei的表达式来计算 b n e w b^{new} bnew。
-
同理得:当 0 < α 2 n e w < C 0<\alpha_2^{new}<C 0<α2new<C时,有:
b 2 n e w = − E 2 − y 1 κ 12 ( α 1 n e w − α 1 o l d ) − y 2 κ 22 ( α 2 n e w − α 2 o l d ) + b o l d ( 9 ) b_2^{new}=-E_2-y_1\kappa_{12}(\alpha_1^{new}-\alpha_1^{old})-y_2\kappa_{22}(\alpha_2^{new}-\alpha_2^{old})+b^{old}\qquad\qquad(9) b2new=−E2−y1κ12(α1new−α1old)−y2κ22(α2new−α2old)+bold(9)
最终的 b n e w b^{new} bnew为:
b n e w = b 1 n e w + b 2 n e w 2 ( 10 ) b^{new} = \frac{b_1^{new}+b_2^{new}}{2}\qquad\qquad(10) bnew=2b1new+b2new(10)
得到了 b n e w b^{new} bnew需要更新 E i E_i Ei:
E i = ∑ S y j α j κ ( x i , x j ) + b n e w − y i ( 11 ) E_i=\sum_{S}y_j\alpha_j\kappa(x_i,x_j)+b^{new}-y_i\qquad\qquad(11) Ei=S∑yjαjκ(xi,xj)+bnew−yi(11)
其中, S S S是所有支持向量 x j x_j xj的集合。
注释: S S S之所以是所有支持向量的集合,是因为初始化的 α \alpha α是一个全为 0 0 0的向量,即 α 1 = α 2 = ⋯ = α m = 0 \alpha_1=\alpha_2=\cdots=\alpha_m=0 α1=α2=⋯=αm=0, w w w的值即为 0 0 0。进行SMO算法时,每轮挑选出两个变量 α i \alpha_i αi,固定其他的 α \alpha α值,也就是说,那些从来没有被挑选出来过的 α \alpha α,值始终为 0 0 0,而根据前面所述,支持向量对应的 α i \alpha_i αi是一定满足 0 < α i ≤ C 0<\alpha_i\leq C 0<αi≤C的。由于不是支持向量的样本点,对应的 α i \alpha_i αi值为 0 0 0,加起来也没有意义,对 w w w产生不了影响,只有支持向量对应的点 ( x i , y i ) (x_i,y_i) (xi,yi)与对应的 α i \alpha_i αi相乘,产生的值才对 w w w有影响。
5.SMO算法总结
【参考文献】
- 刘建平 博客园:https://www.cnblogs.com/pinard/
- 周志华 《机器学习》
- 李航 《统计学方法》

