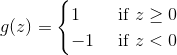支持向量机（SVM）（一）----介绍SVM

    ====================================    

本文根据Andrew NG的课程来梳理一下svm的思路。如有错误，欢迎指正。

==============================================

    支持向量机(Support Vector Machine，SVM)是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析。有很多人认为SVM是最好的监督学习算法。blablabla..........，SVM的思想很简单，为了让SVM更好的分类， 我们的任务就是最大化“间隔”，大量的公式就是为了解决这个最大间隔。

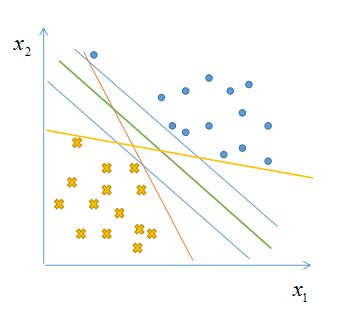
    给定一组数据，该数据集可以分为两类，我们的根本任务就是要找出一个超平面，将这两个类别分别开来。但是这样的超平面可能不止一个（如下图），那么我们怎么才能找出一个最佳的呢？以及如何判断最佳呢？

    直觉来看，上图中绿色划分超平面是最好的，为什么呢？以图来说比较显而易见，对于新来的两个正、负样本，如下图。可能会使得很多超平面分类错误，而中间的绿色超平面却依然可以分类正确，故而他是最鲁棒的，也是泛化能力最强的。

    那么如何求出最佳的呢？我们就要引出“间隔”这个概念。

    函数间隔（functional margin）和几何间隔（Geometric margin）

    我们先说明一下预测结果的可信度。若某一训练样本集中有如下一些样本点，假设其是线性可分的，代表正类，代表负类，图中有三个样本点A,B,C。

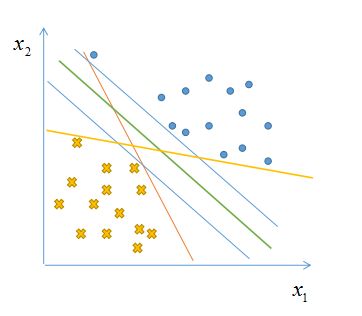
    从图中，我们可以看到C点在划分超平面的上方，并且距离划分超平面很远，直觉上，我们可以很确定的预测，该样本属于正类，其可信度是很高的。对于A点，它也在划分超平面的上方，并且距离划分超平面很近，其预测值同样也为正类，由于其距离划分超平面很近，如果因为某些outlier使得超平面有稍微的变动，那么我们很容易把它预测为负类！所以A点预测的确信度不高。因此，为使得训练样本中的样本分类结果可信度更高，我们就要尽可能使正、负类样本点尽可能的远离划分超平面。如下图的绿色划分超平面，两类样本到它的距离是最远的，故而他是相对最好的。

    为了描述方便，在此用方程来定义超平面。对于给定的样本集合，划分超平面的线性方程可表示为：

    其中，表示超平面的法向量，b表示截距，所以划分平面可以被w和b确定，那么:

    若,在超平面的上方，为正类，若，在超平面的下方，为负类。

    另外，我们引入阶跃函数：

    令，给定一个样本，表示分类结果，则当，,当，。

    函数间隔

    对于给定一个训练样本，我们对该样本的，定义函数间隔（functional margin）为：

    如果该样本的类别，只要越大，那么函数的间隔也就也大，也就是说我们对该样本的分类，即正确，可信度又高。同理，如果，只要越小（是一个负值），那么函数间隔也就越大。因此，一个大的函数间隔可以表达出一个既可信又正确的预测。

    但是对于一个线性可分的集合，我们选择上述分类函数g，此时函数间隔有一个不好的性质，就成倍地放缩w和b时，并没有实际意义的改变，因为，所以的值并没有任何改变，只依赖于的符号，并不依赖于它的变化幅度，因此成倍地放缩w和b没有任何意义。由此我们引入几何间隔。

    我们知道随意放缩w,b并没有实质的改变，那么我们可以把函数间隔的法向量w变为单位向量，截距b同比例放缩， 即：

     之所以这么做是因为，由几何的基本知识可知，某样本点到划分超平面的距离，可表示为：

    我们知道对于正类，有，，对于负类有，，那么我们对距离可以去掉绝对值，则有：

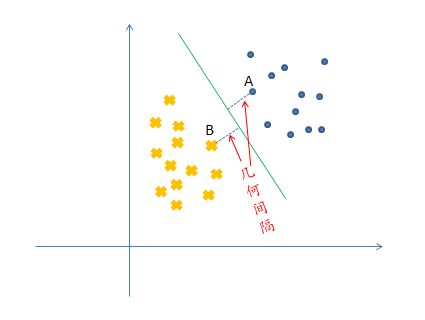
    我们称此式为几何间隔，对于此式我们可以看出来，无论我们怎么放缩w和b，都不会有什么改变，这就克服了函数间隔的弊端。特别地当时，几何间隔与函数间隔是一样的。几何间隔如下图：

    若某样本点满足：或者，则我们称这样的样本点为“ 支持向量”（support vector）。

    到此我们已经说明什么是函数间隔和几何间隔，那么什么是“间隔”呢？我们定义：

    为“间隔”，其表示的意义是两个不同类别的支持向量到划分超平面距离之和，如图所示：

    由此我们可以知道，我们要使分类结果可信度最大，我们就要最大化“间隔”，即：

    但是是非凸的，这对于我们的计算是非常困难的，因此我们要转换他的形式，我们知道最大化等同于最小化因此上式可以转化为：

    这样做的目的，是把原问题转化为凸优化问题，我们有现成的软件可以解决掉它。好了，到此我们把支持向量机求超平面问题转化为求最大间隔问题，而且该问题是凸的。如何解决他呢？请看支持向量机SVM（二）