机器学习----SVM(3)核函数
本文主要参考了了博客:http://blog.pluskid.org/?p=685 更详细的讲解可以参考原博客。
1、为什么引入核函数呢?
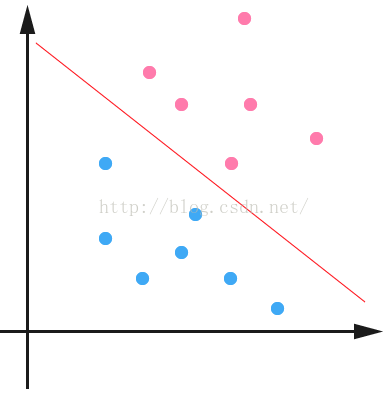
为了回答这个问题,我们先来说明什么是线性不可分数据。如下左图所示,如果数据能用一条直线或一个超平面分开的数据,就是线性不可分数据。那么什么是线性不可分数据呢?如下右图所示,我们无法用一条直线或一个超平面分开的数据。
很不幸的是我们之前介绍的SVM是一个线性分类器,也就是处理线性可分数据,对于上右图的数据前面介绍SVM就无可奈何了。
但是这里有个问题----为什么我们不学习一个针对上右图这种非线性的分类器呢?我个人觉得这样的非线性分类没有通用性,因为线性不可分的情况可能有多种,我们不能针对每一种类型学习一种分类器。因此唯一的办法就是想办法把线性不可分数据转换成线性可分的。
2、怎样将线性不可分数据转换成线性可分的呢?
将低维数据转换成高维数据,就可以实现将线性不可分数据转换成线性可分的。我们以上右图为例。
对于上右图的数据,一个一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用 X1 和 X2 来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:
![]() (1)
(1)
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2,那么显然,上面的方程在新的坐标系下可以写作:
![]() (2)
(2)
说明:对上面做个简单的解释。X1,X2是二维平面的两个轴,x轴和y轴。(1)式是二维平面圆的表达式,如果我们把X1, X1^2,X2,X2^2, X1X2五个变量看成新的轴,就可以得到(2)式。我们发现(2)式在5维空间中是一个超平面。这样我们就右回到求解超平面的问题了。是不是很开心呢?
3.维度爆炸怎么办?核函数隆重登场
也许有人已经发现了,二维线性不可分数据转换成线性可分需要转换到五维,那如果维度变大,转换后的维度岂不是更大了,甚至是无穷维。这样我们就根本没有办法计算了。这时核函数就隆重登场了。核函数的目的就是在低维计算但是效果等同于在高维计算,这样就可以简化我们的计算了。这里偷个懒贴两张图片吧。
从上面我们可以看到二维到五维的转化,我们只需要在低维计算,就可以实现和在高维运算一样的结果,这就是和函数的作用。
我们把这里的计算两个向量在映射过后的空间中的内积的函数叫做核函数 (Kernel Function) ,例如,在刚才的例子中,我们的核函数为:
![]() (3)
(3)
4、SVM中怎样用核函数呢?
先回顾一下我们最原始的分类函数,![]() ,根据上一篇博客(7)式有
,根据上一篇博客(7)式有![]() ,则分类函数变成了:
,则分类函数变成了:
![]() (4)
(4)
上式中
上式中的x还是二维的,映射到五维后的分类函数为:
![]() (5)
(5)
同理,我们上一篇博客最后得到的目标函数转换到五维空间后得到:
![]() (6)
(6)
我们将前面定义的核函数的形式也就是(3)式,带入(6)中有下式:
![]() (7)
(7)
这样一来,我们就不用在高维空间计算了。
但是有个问题,前面我们说的映射是我们手工构造的,那对于其他数据我们怎样构造映射呢?还好核函数的类型并不是很多,我们只要选择自适合自己数据的就可以了。
5、核函数的类型
1、多项式核,显然刚才我们举的例子是这里多项式核的一个特例(R=1,d=2)。虽然比较麻烦,而且没有必要,不过这个核所对应的映射实际上是可以写出来的,该空间的维度是
![]() ,其中 m 是原始空间的维度。
,其中 m 是原始空间的维度。
2、高斯核![]() ,这个核就是最开始提到过的会将原始空间映射为无穷维空间的那个家伙。不过,如果 σ 选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果 σ 选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数 σ ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。
,这个核就是最开始提到过的会将原始空间映射为无穷维空间的那个家伙。不过,如果 σ 选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果 σ 选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数 σ ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。
3、线性核 κ(x1,x2)=⟨x1,x2⟩ ,这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了。
总结:(借大神之言)对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。由于核函数的优良品质,这样的非线性扩展在计算量上并没有比原来复杂多少,这一点是非常难得的。当然,这要归功于核方法——除了 SVM 之外,任何将计算表示为数据点的内积的方法,都可以使用核方法进行非线性扩展。