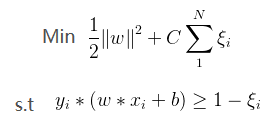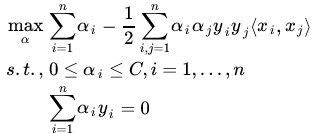机器学习算法之 支持向量机( SVM )之SMO方法

 本文记录最成功的监督机器学习算法之一，支持向量机SVM（Support VectorMachines）之SMO（Sequential Minimal

Optimization）序列最小化算法算法。

过程中处了图书，参考了不少csdn博客，整理下整个过程记的理解，包括推理、迭代、代码等
 
 

1、SVM原理简述

 
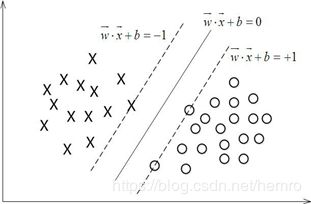
 如下图，两种类型数据点可以通过一条直线分开，叫做线性可分。如果数据点为二维分割线为一条直线，三维的一个

平面，更高维平面上就会是其他的分界表现形式，将这个分界称为超平面（hyper plane）。

 线性分类器的学习目标便是要在n维的数据空间中找到一个分界使得数据可以分成两类，即寻找最佳分隔超平面，找到离超

平面距离最近的那些点，这些点称作为支持向量，再从这些点到分隔面的距离最大化。就是寻找最佳分隔面。

 分隔超平面表示为 Wtx+b=0（ w为法向量，x为数据点，b为常数） 当Wtx+b >0 时对应数据类型1，Wt*x+b >0 时对应数据

类型-1，等于0时落再分隔面上不能区分了。

 怎么确定最佳分隔超平面，下面以以二维平面为例，看看SVM的原理。如下图，不难发现能够实现分类的超平面（二维平面

上就是一条直线）会有很多条，如何确定哪个是最优超平面呢？直观而言，最优超平面应该是最适合分开两类数据的直线。而判定

“最适合”的标准就是这条直线距直线两边最近数据的间隔最大，也就是“使样本中离超平面最近的点到超平面的距离最远”–最大间隔。

所以，得寻找有着“最大间隔”的超平面。下面的问题是–如何求“最大间隔”

2、寻找最大间隔

 在超平面wx+b=0确定的情况下，|wx+b|能够表示点x到距离超平面的远近，而通过观察w*x+b的符号与类标记y的符号是否一致

可判断分类是否正确（这是为什么类别标签采用+1和-1，而不是不是0和1的原因，除了这个下面会看到采用+1和-1后我们可以统一的

公式来表示数据点到分隔面的距离），所以，可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔

（functional margin）的概念。

定义函数间隔为：

再假设

为T中所有样本点(xi，yi)中具有最小距离的数据点，而

这些数据点也就是前面提到支持向量。为什么定义这个后面再讲。

 但这样定义的函数间隔有问题，即如果成比例的改变w和b（如将它们改成2w和2b），则函数间隔的值f(x)却变成了原来的2倍（

虽然此时超平面没有改变），所以只有函数间隔还远远不够。

几何间隔

 几何间隔可以|WtA +b|/||W||来表示，推导过程

假定对于一个点 x ，令其垂直投影到超平面上的对应点为 x0 ，w 是垂直于超平面的一个向量，为样本x到分类间隔的距离，如下图所示：

有，||w||^2=wT*w，是w的二阶泛数。
又由于 x0是超平面上的点，满足 f(x0)=0 ，代入超平面的方程即可算出：

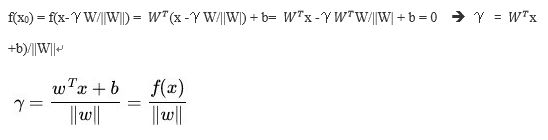
数据点到超平面的几何间隔定义为：

几何间隔就是函数间隔除以||w||，可以理解成函数间隔的归一化。
 
 

寻找最大间隔

 找到描述超平面和数据点的间隔的公式（即几何间隔）后，我们来看寻找最大间隔优化问题。首先找到具有最小间隔的数据点，

即前面提到的支持向量，然后再这些点和超平面的间隔最大化。即：

换做上面的记法

 
转化为最小求解问题

 
 

3、推理过程 - 拉格朗日乘子法、KKT条件、对偶问题

3.1KKT条件

 
先看下KKT条件

假设有一个优化问题：

其中f(x)是原目标函数，hj(x)是第j个等式约束条件，λj是对应的约束系数，gk是不等式约束，uk是对应的约束系数。

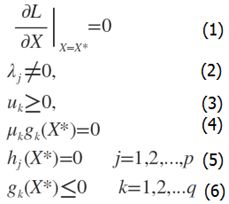
 这些求解条件就是KKT条件。(1)是对拉格朗日函数取极值时候带来的一个必要条件，(2)是拉格朗日系数约束（同等式情况），

(3)是不等式约束情况，(4)是互补松弛条件，(5)、(6)是原约束条件。

 将上述带约束的优化问题转化为无约束优化问题, 定义拉格朗日(Lagrangian)函数如下:

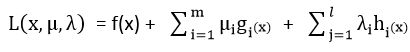
令

z(x)满足原始约束条件的x, 其值等于f(x)
满足初始约束,拉格朗日函数变成:

 
 

3.2目标函数

 
好，我们再回到我们目标优化函数

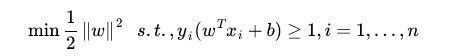
KKT条件变成以下拉格朗日函数，其中

再通过对偶性：

先求最大值，后求最小值，求最小值时，将是w,b的函数了。极值在导数为0的点处取到（KKT条件一部分），因此分别求L对w,b的导数，并令其为0，得如下结果。

把这结构带入到L

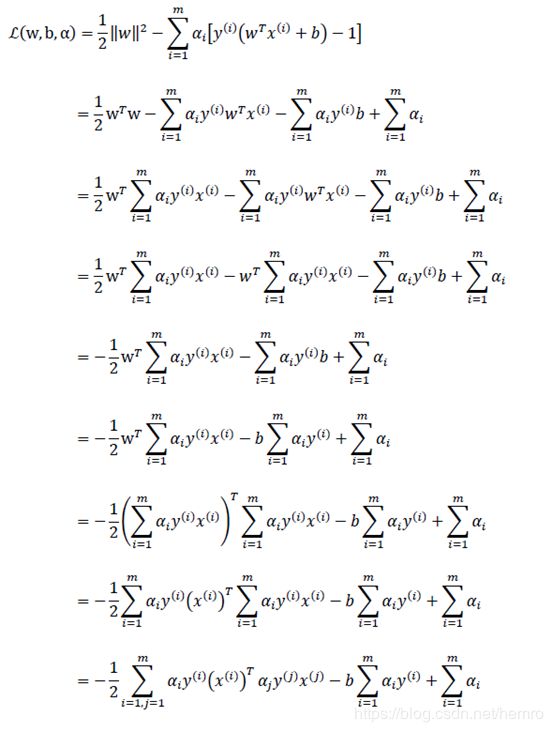
最终得到

那么我们优化函数最终变成

此外，从KKT条件应该满足：

(1)，(3) KTT转化约束条件，(2) 原始条件

变化下符号变成极小值

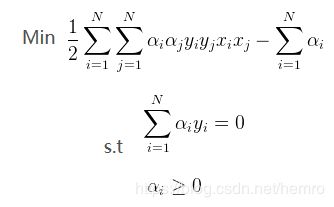
最终求得结果后，可以反过来求解得到w和b的值。

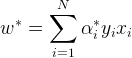
增加松弛变量

目标函数增加一个松弛变量

最终变成


 
 

4、核函数

 
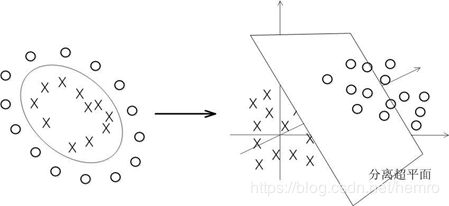
 数学原理：数据映射到高维空间上，最简单的如下，从二维空间的数据映射到三维空间使得线性可分。原则上任意数据都可以

通过高维空间映射线性可分，可以映射到无穷维空间，当然维度过大后出现一个非常严重问题，过拟合，这个后面再讲

 核函数的作用是避免底维到高维映射，维度爆发性增长，从而增加计算复杂度，甚至无法计算。核函数作用就是事先在底维

空间上计算，而实际分类在表现在高维空间上，避免了直接在高维空间中的复杂计算。

 特征空间的映射：低维空间到高维空间映射

 如下二分类问题，分别分布为两个圆圈的形状，这样的数据本身就是线性不可分的，此时咱们该如何把这两类数据分开呢？

一个理想的分界应该是一个“圆圈”而不是一条线（超平面）。如果用和来表示这个二维平面的两个坐标的话，我们知道一条二次曲线

（圆圈是二次曲线的一种特殊情况）的方程可以写作这样的形式：

因此我只需要把它映射到后的结果，将坐标轴经过适当的

旋转，就可以很明显地看出，数据是可以通过一个平面来分开的

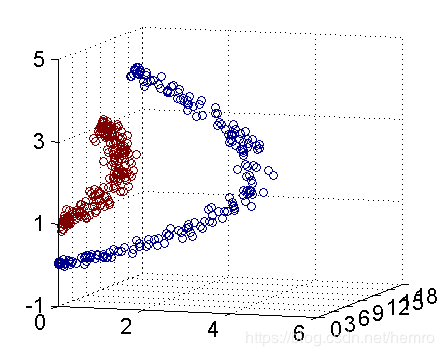
核函数相当于把原来的分类函数：

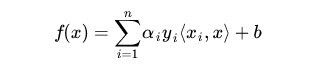
映射成：

而其中的可以通过求解如下 dual 问题而得到的：

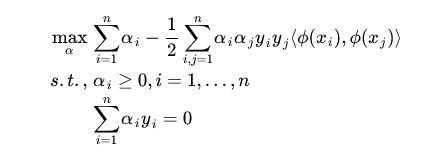
 这样一来问题就解决了吗？似乎是的：拿到非线性数据，就找一个映射，然后一股脑把原来的数据映射到新空间中，再做线性

SVM 即可。回想上面的例子。我们对一个二维空间做映射，选择的新空间是原始空间的所有一阶和二阶的组合，得到了五个维度；

 如果原始空间是三维（一阶、二阶和三阶的组合），那么我们会得到：3(一次)+3(二次交叉)+3(平方)+3(立方)+1(x1x2x3)+2*3

(交叉，一个一次一个二次，类似x1*x2^2) = 19维的新空间，这个数目是呈指数级爆炸性增长的，这个给计算带来非常大的困难，

而且如果遇到无穷维的情况，就根本无从计算了。

 这时需要Kernel函数了，

 我们把这里的计算两个向量在隐式映射过后的空间中的内积的函数叫做核函数 (Kernel Function) ，例如，在刚才的例子中，我们的

核函数为：

 核函数能简化映射空间中的内积运算——刚好“碰巧”的是，在我们的 SVM 里需要计算的地方数据向量总是以内积的形式出现的。

对比刚才我们上面写出来的式子，现在我们的分类函数为：

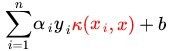
其中由如下 dual 问题计算而得

 
 

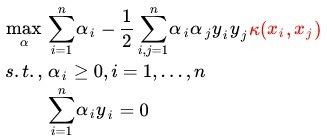
5、迭代过程

 
 上一节叙述了推理过程，但具体算法迭代过程没有讲，如怎么计算a、w、b及迭代，从而得到最终w和b。下面看SMO算法详细

求解过程：
 
 

5.1转化为两个乘子的优化

 
 首先回归前面得到最终结果

改变为最小化问题
(1)

 
 

5.2优化方向

 
 

5.3 求解alpha2 new取值范围

 
 

5.4 求解alpha2 new

 
 

5.5 求解alpha1 new

 
 

5.6 求解b的值

 
 

5.7 分类函数

 
 

6、代码实例

 
看一个实例代码，前面推理过程理解之后代码本身不复杂。一个训练简单svm smo函数

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
    b = 0; m,n = shape(dataMatrix)
    alphas = mat(zeros((m,1)))
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0
        for i in range(m): #每次取一个条数据，对应的alpha1
            fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b #计算分类函数结果，直接套用分类函数公式(8)
            Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions  #计算结果和实际分类的差
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
               #这里用到迭代中不满足KKT条件的3个柜子，((labelMat[i]*Ei > toler) and (alphas[i] > 0)为例，假设此次为正分类，那么(labelMat[i]*Ei > toler)
               # Ei>0 并且Ei > toler，因为labelMat[i]=1， 从而得到yi*fXi>1, 此时alpha1>0则是不满足的，而原本alpha1=0
                j = selectJrand(i,m)
                fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b # alpha2随机选择
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                if (labelMat[i] != labelMat[j]):  # y1和y1不同符号，计算L和H
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print "L==H"; continue
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T #计算η
                if eta >= 0: print "eta>=0"; continue  #计算η =0 时，被0除，暂时这种情况跳过
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta #计算alpha2，参考公式(5)
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; continue  #达到优化门限
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
                                                                        #the update is in the oppostie direction  更新alpha1，公式(6)
                #计算b1,b2，公式(7)                                                        
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
        if (alphaPairsChanged == 0): iter += 1
        else: iter = 0
        print "iteration number: %d" % iter
    return b,alphas