机器学习(2) - SVM 推导
SVM的核函数,这里还剩一个核函数。
整个SVM比较难以理解的地方就是拉格朗日对偶求极值。整体感觉难点就是一个对偶性的问题,数学推导比较麻烦,坑太深,适合理论研究。网友的一些关于数学的理解和讨论还是比较有意思。
【Winston SVM课程总结】
【整体流程总结】
【对偶性,优化目标推导】
【参考链接】
1 : 这篇博客主要介绍了对偶性和拉格朗日乘子,Duality and Lagrange multipliers
https://www.svm-tutorial.com/2016/09/duality-lagrange-multipliers/
一个推导还行,一个有一个流出图总结的不错
2 : https://zhuanlan.zhihu.com/p/28804123
3 : https://zhuanlan.zhihu.com/p/33940537
4: http://jermmy.xyz/images/2017-12-23/support_vector_machines_succinctly.pdf -----老外的书,写的还是比较详细
5:https://zhuanlan.zhihu.com/p/26514613 KKT条件,判断是否是最优解
MIT Winston的教程是简化了推导,只关注了再gutter上的点,把不等式的约束条件,变成了等式约束条件,所以容易理解。关于拉格朗日对偶, 实际上Winston只关注了gutter上的点,回避了带不等式约束问题的求解,只考虑等式的情况。感觉数学公式模型建立好了以后,后面的工作就是数学优化的问题了,还是需要很多凸优化和数值计算的知识。数学优化方面,定理和公式坑太多。莫名其妙的上界证明。
【思考总结】
(1) 为什么要用对偶,为什么要把本来一个minmax问题转换为maxmin问题,网上解释五花八门,有说能把向量点乘导出,然后才能导出核函数。有的说方便求解,在参考链接1中的说法是,It turns out that sometimes, solving the dual problem is simpler than solving the primal problem.根据参考文献1,对偶性实际上就是本来求一个函数的极小值,转而求另外一个函数的极大值
实际上就是上面总结的两个优点:第一可以减少算法复杂度,第二在之后引入不同的kernel时从数学上讲更加自然
(2) 关于winston只考虑gutter上点的一些疑问: 如果只考虑gutter上点,也是能推导,只是最后全部剩下a的时候,怎么认为是max关于a的二次项目,因为这时候是一个带等式约束条件的,求极小值的问题。而且另外一个比较关键的问题是如果只认为是取边界上的点,那么实际上限制条件不是针对所有的点,而是边界上的点,问题是起初是不知道边界上有哪些点存在,所以是前提条件没有的问题。这里如果数学功底不强在设计算法的时候只能是找几个toy数据来进行试验,最后总结出规律。
(3)Lagrange multiplier方法总结--等式约束情况下
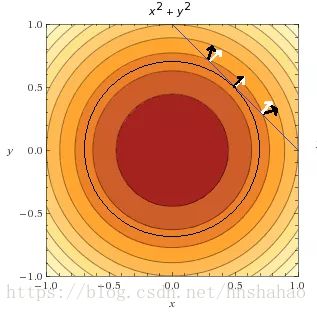
This function L called the Lagrangian, and solving for the gradient of the Lagrangian (solving ∇L(x,y,λ)=0,∇L(x,y,λ)=0) means finding the points where the gradient of f and g are parallel
在等式约束下,极值点是使得f函数和g函数在极值位置有平行梯度的点,满足一个λ的系数关系。这幅图展示的是带等号约束条件下,拉格朗日乘子法的原理。
(4)对偶问题成立和最优值唯一的条件
对偶性等价条件,意味着原始问题的解和对偶问题的解是同一解,这个是用Slater定理证明
另外KKT的定理保证了解是最优解
To sum up, if a solution satisfies the KKT conditions, we are guaranteed that it is the optimal solution
对于含有不等式约束的优化问题,如何求取最优值呢?常用的方法是KKT条件,同样地,把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + a*g(x)+b*h(x),KKT条件是说最优值必须满足以下条件:
1. L(a, b, x)对x求导为零;
2. h(x) =0;
3. a*g(x) = 0;
求取这三个等式之后就能得到候选最优值。其中第三个式子非常有趣,因为g(x)<=0,如果要满足这个等式,必须a=0或者g(x)=0. 这是SVM的很多重要性质的来源,如支持向量的概念
【后续可以继续研究的参考资料】
SMO----https://zhuanlan.zhihu.com/p/29212107 介绍SMO
SVM----https://zhuanlan.zhihu.com/p/31131842 SVM介绍的还行,关于对偶怎么得出的和我的思路类似
KKT条件 -- https://blog.csdn.net/xianlingmao/article/details/7919597 比较简单
拉格朗日对偶 --- https://www.zhihu.com/question/58584814 这里面的第二个解释,数学性比较好