目标分割(四)DeepLab v1讲解

原文：Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs
收录：ICLR 2015 (International Conference on Learning Representations)
          其中DeepLab 是由Google团队提出的，至今有四个版本(v1-v4)
 

---

 

ABSTRACT

        论文是通过结合深度卷积神经网络(DCNNs) 和概率图模型(DenseCRFs) 来解决像素级分类问题。

       Q1：由于DCNNs高级特征的平移不变性(即高层次特征映射)，实验中发现DCNNs的最后一层响应在做语义分割时精准度不够，怎么处理？
       A1：将DCNNs最后一层的响应和完全连接的条件随机场(CRF)结合。

• 定性上说，DeepLab对于边界的分割精度超过之前的方法。
• 定量来说，本文将PASCAL VOC-2012语义分割的准确率提高，在测试集上IOU准确率达到了71.6%。

       Q2：如何高效实现并获得结果？
       A2：将hole（即空洞卷积）算法应用到DCNNs模型上，最后在现代GPU上运行速度达到了8FPS。

 
※论文核心思想：

1. 将DCNNs的特征图与全连接CRF结合；
2. Hole（空洞卷积）应用在DCNNs中；

---

 

1. INTRODUCTION

       尽管深度卷积网络(DCNN)就在1998年被提出并被LeCun等人应用到了手写文件识别中，但直到最近，DCNN在高维视觉应用中才成为了主流。在过去两年，DCNNs将一系列高维应用的计算机视觉系统的性能提升到了一个新的高度，比如图像分类、目标检测、细粒度分类等。

       相比于传统视觉算法(SIFT或HOG)，DCNN以端到端(end-to-end) 的方式获得了很好的效果。主要归功于DCNN对图像转换的平移不变性(invariance) ,由于平移不变性增强了对数据分层抽象的能力，但同时会阻碍低级(low-level)视觉任务,例如姿态估计、语义分割等，因为在这些任务中更倾向于精确定位而不是抽象空间关系。

DCNN在图像标记任务中存在两个技术问题：

       Q1：由于DCNN中重复的最大池化和下采样造成分辨率下降，怎么处理？
       A1：通过 空洞算法(atrous) 来扩展感受野，获取更多的上下文信息。

       Q2：分类器获得以对象为中心的决策需要空间不变性，从而限制DCNN的空间定位精度
       A2：通过 条件随机场（DenseCRF） 提高模型捕获细节和边缘信息的能力

DeepLab有三大优点：

• 快速：使用atrous算法的DenseDCNN可以保持8FPS的速度，全连接CRF平均推断需要0.5s
• 精确：在PASCAL语义分割中获得了第一，比第二名(Mostajabi et al 2014)准确度多7.2%
• 简单：DeepLab由两个成熟的模块(DCNN和DenseCRF)级联而成

---

2. RELATED WORK

       DeepLab直接工作在逐像素分类，类似于FCN(Fully convolutional networks for semantic segmentation)，这与使用两阶段的DCNN方法形成对比(指R-CNN等系列的目标检测)，这种技术通常使用自底向上的图像分割和基于DCNN的区域分类的级联方法，R-CNN一系列的做法是在原图上获取候选区域(region proposal)，再送到DCNN中获取分割，重新排列得到结果，但是如果前端分割出现错误，则网络整体都会受到影响。虽然R-CNN一系列不断尝试处理前段分割算法的本质，但R-CNN没有完全利用DCNN的特征图。

       接下来研究人员已经开始考虑利用DCNN卷积计算的特征来进行密集图像的标记，虽然这些工作中分割算法与DCNN分类器的结果仍然是不挂钩(解耦)的，但我们认为只在后阶段进行分割是有利的，避免了过早决策对结果的影响。

       最近，对于DCNN的运用，第一种：FCN（2014）直接以滑动窗口的方式将DCNNs应用于整个图像，将DCNN最后全连接层替换为卷积层。为了处理开头所说的空间定位问题，他们对中间特征映射的分数进行上采样和级联。第二种：Eigen & Ferguez(2014)则是将粗糙的结果传递到另一个DCNN，从而将预测结果从粗到细进行细化。

       我们的模型与其他先进模型的主要区别在于DenseCRFs和DCNN的结合。我们将每个像素视为CRF节点，利用远程相关性，使用CRF推理直接优化DCNN的损失函数。Koltun(2011)的工作表明完全连接的CRF在语义分割下非常有效。

       也有其他组也采取非常相似的方向(DCNN和密集的CRF结合)

---

3. CONVOLUTIONAL NEURAL NETWORKS FOR DENSE IMAGE LABELING

       在此，我们描述如何重新使用和优化现有的Imagenet预训练的16层分类网络(Simonyan & Zisserman, 2014) (VGG-16)，使其成为一个高效的密集特征提取器，用于我们的密集语义图像分割系统。
       空洞算法好处：①能够密集特征提取，获取更多的上下文信息；②控制感受野大小，加快运算速率。

 

3.1. 利用空洞算法实现高效的密集滑动窗口特征提取

 
       由于密集空间特征图的正确评估是密集CNN特征提取器的基础

       作为实现这一目标的第一步，我们将VGG-16的全连接层FC转换成卷积层Conv，并以卷积方式在其原始分辨率的图像上运行网络。但这还不够，因为它产生非常稀疏的检测分数(stride = 32 pixels)。为了在我们目标步幅stride=8pixels上更密集地计算分数scores，我们开发基于Giusti、Sermanet以前使用方法的变体。我们在VGG网络中最后两个max-pooling之后跳过subsampling(下采样)，并通过引入零来修改随后各层的卷积滤波器，以增加其长度（在最后三个Conv中为2×，在第一个FC为4×)。我们可以通过保持过滤器不加改动来高效的实现这个操作(使用空洞算法)，而不是分别使用2或4像素的步幅稀疏地对特征图进行采样。

---

重点：※空洞卷积的理解

       ①首先简单介绍1-D图像下空洞卷积在卷积神经网络的使用(在DeepLabv3中有更详细的讨论)。
              
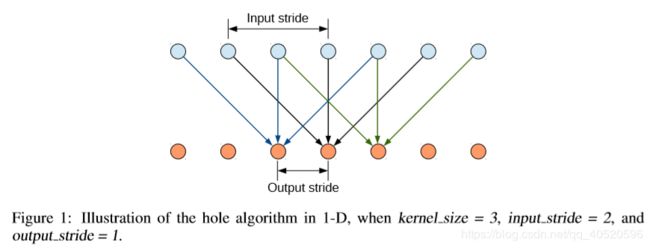
       ②在2-D图像上应用空洞卷积：
                                                        
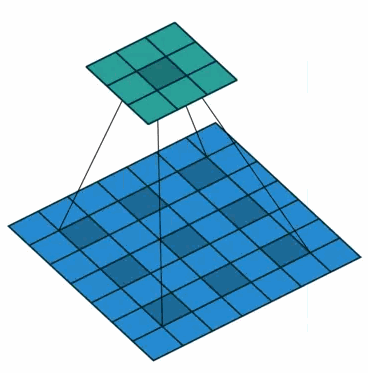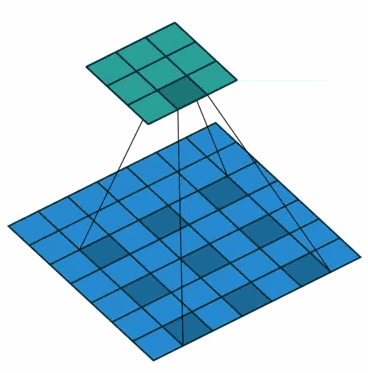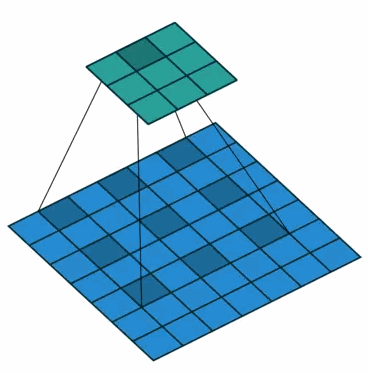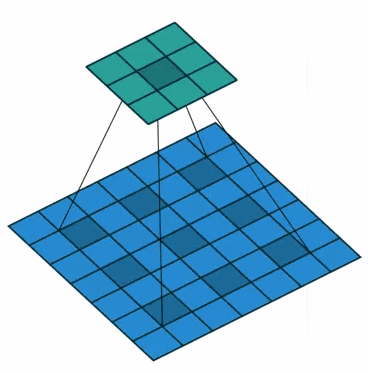
          蓝色部分是输入：7×7的图像；
          青色部分是输出：3×3的图像；
          空洞卷积核：3×3采样率(扩展率)为2 无padding。

       ③为什么空洞卷积更好，有什么好处？

              特征图变小主要是由于卷积层和池化层引起的，若令所有层的stride=1，输出feature map将会变大。

       情况一：原始情况下，Pooling layer(stride=2)，最后得到的感受野RF(receptive field) = 4；
                            
       情况二：若令Pooling layer(stride=1)，虽然输出更密集，但是感受野RF(receptive field) = 3，感受野变小；
                                

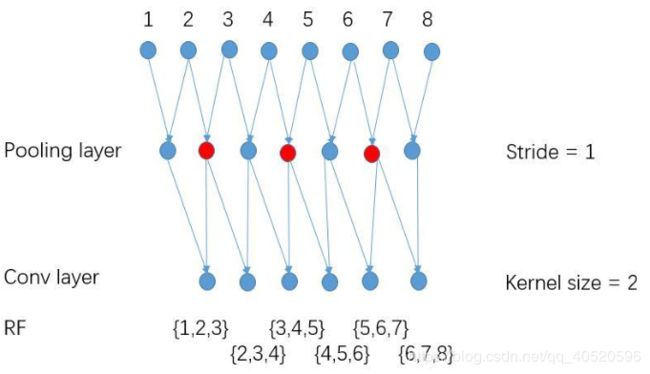
       情况三：若令Pooling layer(stride=1)，并且使用空洞卷积，好处则是感受野不变仍然是4，且输出更密集。
                             

---

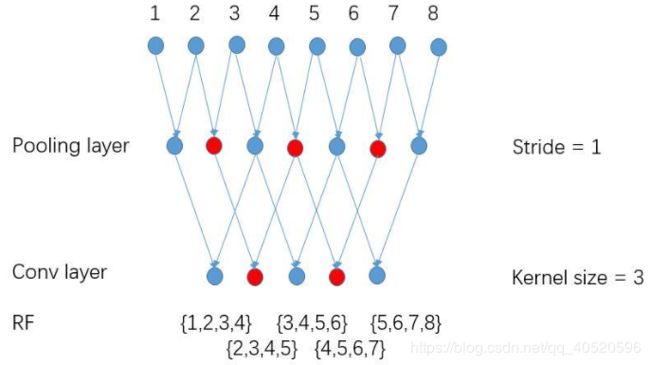
       我们微调Imagenet预先训练的VGG-16网络的模型权重，以简单的方式适应图像分类任务，遵循Long（FCN）等人的方式。 我们用21路替换最后一层VGG-16中的1000路Imagenet分类器。 我们的损失函数是CNN输出图中每个空间位置的交叉熵项的总和（与原始图像相比下采样了8倍）。所有位置和标签在整体损失函数中的权重相等。 我们的目标是真实值标签（8倍下采样）。 我们通过Krizhevsky等人的标准SGD程序来优化所有网络层的权重的目标函数。

3.2. 利用卷积网控制感受野大小，加速密集计算

       使用我们的网络进行密集分数计算的另一个关键因素是明确控制网络的感受野大小
密集分数图像计算存在两个实际问题：
       Q1：在我们考虑的VGG-16网络的情况下，如果网络应用卷积，其感受野是224×224（零填充）和404×404像素。 我们认为这种感受野大小太大，无法保证良好的定位精度；
       Q2：将网络转换为完全卷积的网络之后，第一个全连接层具有4,096个大的7×7空间大小的滤波器，并且成为我们密集分数图计算中的计算瓶颈。
       A：将第一个FC层空间抽样到4×4空间大小，这样之后能够将网络的感受野减少到128×128（零填充）或308×308（卷积模式），并将第一个FC层的计算时间缩短了3倍。

---

4. DETAILED BOUNDARY RECOVERY : FULLY-CONNECTED CONDITIONAL RANDOM FIELDS AND MULTI-SCALE PREDICTION

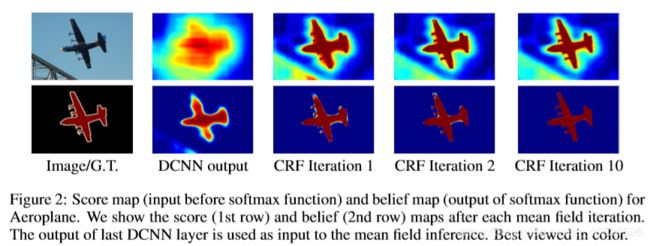
       如上图所示，DCNN可以可靠地预测图像中物体的存在和大致位置，但不太适合精确地定位它们的轮廓，在卷积网络中，分类精度和定位精度之间存在一种自然的平衡：例如具有多个max-pooling层的深度模型已被证明在分类任务中最成功，但是在定位方面效果不好。
       近期工作从两个方向来解决这个定位的挑战。 第一种方法是利用卷积网络中多层的信息来更好地估计对象边界(例如FCN)。 第二种方法是采用超像素表示，本质上是将定位任务委托给低层次的分割方法(例如Feedforward semantic segmentation with zoom-out features)。而我们则是通过耦合DCNN的识别能力和完全连接的CRF的细粒度定位精度来寻求新的替代方向，并表明它在解决定位挑战方面非常成功，产生了准确的语义分割结果， 以超出现有方法的详细程度恢复对象边界。

4.1. 全连通条件随机域CRF精确定位

       传统上，条件随机域(CRFs)已被用于平滑噪声分割图。通常，这些模型包含耦合相邻节点的能量项，有利于相同标签分配空间近端像素。定性的说，这些短程的CRF主要功能是清除在手工特征基础上建立的弱分类器的虚假预测。

       由上图可知，得分图通常相当平滑并产生均匀分类结果,使用短程CRFs可能是有害的，因为我们的目标应该是恢复详细的局部结构，而不是进一步平滑它。使用对比敏感能量函数(Rother et al.， 2004)结合局部范围的CRFs可以潜在地改善局部化。
 
       为了克服短距离CRF的这些限制，我们将我们系统与Krahenbuhl＆Koltun（2011）的完全连接的CRF模型相结合。该模型采用能量函数
                            
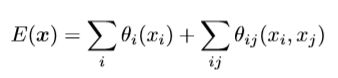
其中 x 是像素的分配标签，上面公式分为一元势能函数θ_i(x_i)和二元势能函数θ_ij(x_i,y_j)。

一元势能函数：
                                                 ${\Theta }_i(x_i)=-logP(x_i)$
 
                     其中$P(x_i)$为DCNN对像素 i 处分配的标签的概率
 
二元势能函数：刻画变量之间的相关性以及观测序列对其影响，实质是像素之间的相关性，对于图像中的任意一对像素 i 和 j ，无论它们之间的距离有多远，
                        即模型的因子图是完全连通的。
                                   ${\Theta }_{ij}(x_i,x_j)=\mu (x_i,x_j){\sum }_{m=1}^K{\omega }_m{k}^m(f_i,f_j)$
 
                     其中$\mu (x_i,x_j)=1$           (当$x_i\ne x_j$)
                            $\mu (x_i,x_j)=0$           (当$x_i=x_j$)             即Potts模型
                            $k^m$ 是高斯核，取决于为像素 i 和 j 提取的特征(表示为 f )，并由$w_m$加权，由于采用位置和颜色组合，因此内核：
 
                            $k^m=w_{1}exp(-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\alpha }^2}-\frac{||I_i-I_j|{|}^2}{2{\sigma }_{\beta }^2})+w_{2}exp(-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\gamma }^2})$
                     其中 p 表示像素位置， I 表示像素颜色强度，超参数σ_α，σ_β，σ_γ控制高斯核的“尺度”。

 

4.2. 多尺度预测

       继Hariharan.2014( Hypercolumns for object segmentation and fine-grained localization )和Long(FCN)的最新成果之后，我们还探讨一种多尺度预测方法来提高边界定位精度。具体来说，我们将前四个最大池化层中的每一个的输入图像和输出附加到一个两层多层感知机MLP(第一层是128个3×3卷积，第二层是128个1×1卷积)，其特征图连接到主网络最后一层特征图，最终输出的特征映射送到模型的最后一层辅助预测，合起来模型最后的softmax层输入特征多了5×128=640个通道，实验表示多尺度有助于提升预测结果，但是效果不如CRF明显。

 

Reference

1. 谷歌——DeepLab v1
2. 语义分割丨DeepLab系列总结「v1、v2、v3、v3+」