人体姿态2019（六）Unsupervised 3D Pose Estimation with Geometric Self-Supervision

原文：Unsupervised 3D Pose Estimation with Geometric Self-Supervision
收录：CVPR2019
代码：Pytorch

---

Abstract

不需要任何多视图图像数据，3D骨架，2D-3D点之间的对应关系，或使用之前所学习的3D先验。在训练期间，恢复的3D骨架被重新投影到随机的摄像机视点上，以产生新的“合成”2D姿态。通过将合成的2D姿态提升到3D，并在原始的相机视图中重新投射它们，我们可以定义自我一致性缺失3dandin2d
训练使用自监督方式，对 升维—投影—升维 过程的几何一致性来进行监督，但仅通过自一致性(self-consistency) 不足以生成逼真的骨架，但添加一个2D姿态鉴别器可以使lifter输出有效的3D姿态。

---

 
主要贡献：

• 受 Can 3D Pose be Learned from 2D Projections Alone? 的影响，提出一种将2D关节提升到3D骨架的无监督算法，不使用任何形式的3D数据，只通过观察真实的2D姿态样本来实现3D构建；
• 本文发现： 自一致性 是2D到3D升维过程的必要而不充分条件，当自一致性损失与对抗损失相结合时，可以提高网络性能；
• 提出一种 2D域适应技术，可以利用不同域的数据来提高目标域上的性能；
• 本文发现在训练中增加一个 时间判别器 可以进一步提高性能。

---

1. Unsupervised 2D-3D Lifting

 

Denotation	Meaning
xi $=(x_i,y_i)，i=1,\dots ,N$	N个2D位姿地标，其中根关节(髋关节之间的中点)位于原点
Xi	每个2D关节点对应的3D关节点位置
Xr	生成3D骨架的根关节点坐标
R	随机旋转矩阵
Yi	旋转之后的3D关节点位置
Q(Xi)	Transformation，从 X 到 Y 的变换
P(Yi)	透视投影，yi = P(Yi)
D(yi)	2D姿态判别器
T(·)	时间序列上的2D姿态判别器

       假设一个以原点(0,0,0)为中心、单位是焦距的照相机，并且将骨架到摄像机的距离固定为一个恒定的c单位，此外，本文对2D骨架进行标准化，使头关节到根关节的平均距离为1/c，这样生成3D骨架的头关节到根关节的距离将是1 unit。

---

1.1. Lifting Network

       Figure 1.的 Lifting Network 表示为G(x)，输出每个2D关节点的3D关节位置：

                                                                                $G_{{\theta }_G}($x$)=$ X

        where ${\theta }_G$ are the parameters of the lifter learned during training. 由于从2D到3D还需要深度信息，那么该部分网络还输出每个关节的深度偏移量 $d_i$，参考面是距离 c 个单位的平面。

                                                                          $z_i=max(1,c+d_i)$

        最后得到的3D点 X_i = [$z_i{x}_i,z_i{y}_i,z_i$]。

---

1.2. Random Projections

        将生成的3D骨架按随机相机方向投影到2D上，然后将2D姿态都输入到 Lifting Network 以及 鉴别器，R 则是通过均匀采样[-π, π]之间的方位角和[-π/9, π/9]之间的倾斜角来创建。

---

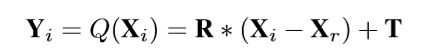
1.3. Self-Supervision via Loop Closure

        通过观察Figure 1.就大致能明白整个工作流程，对于这部分环形闭合结构的损失函数：
                                                                                $L_{3D}={\Vert Y-\tilde{Y}\Vert }^2$

                                                                                $L_{2D}={\Vert x-\tilde{x}\Vert }^2$

---

1.4. Discriminator for 2D Poses

        The 2D pose discriminator $D$ is a neural network (with parameters ${\theta }_D$) that takes as input a 2D pose and outputs a probability between 0 and 1. It classifies between real 2D poser (target probability of 1) and fake (projected) 2D pose y (target probability of 0).

                                      ${\min }_{{\theta }_G}{\max }_{{\theta }_D}{L}_{adv}=E(log(D(r)))+E(log(1-D(y)))$

---

1.5. Temporal Consistency

        注意，本文提出的方法不需要视频数据来进行训练。然而，在可行的情况下，2D位姿时间序列(如动作视频序列)可以提高单帧2D-3D网络的精度。通过利用时间平滑性以及附加的损失函数来优化 Lifting Network G(·) ，如图3所示。

       对于额外的鉴别器 T(·)，其损失函数为：

                                      ${\max }_{{\theta }_T}{L}_T=E(log(T(r_t-r_{t+1})))+E(log(1-T(y_t-y_{t+1})))$

---

1.6. Learning from 2D Poses in the Wild

       为了提高目标域的3D提升精度(例如Human 3.6M，x_t)，我们希望增加2D训练数据 from in the wild(例如OpenPose joint estimates on Kinetics dataset, x_s)，本文训练一个2D域适应网络 C 来将2D关节点目标域与2D关节点源域进行匹配，设x_sc表示校正后的2D关节点源域，那么就有：
                                                                                    x_sc = x_s + C(x_s)

                               ${\min }_{{\theta }_C}{\max }_{{\theta }_{D_D}}{L}_{adv}=E(log(D_D(x_p)))+\lambda {\Vert C(x_s)\Vert }^2+E(log(1-D_D(x_{sc})))$