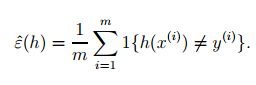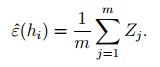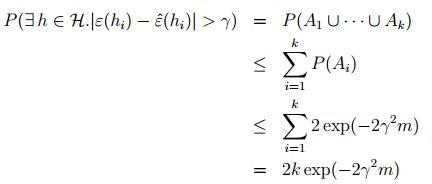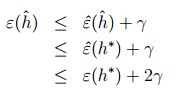机器学习笔记8——ERM
前言:在之前几章中我们已经了解到了很多算法,也知道了在人工智能领域中最强大的机器学习的工具。接下来需要理论结合实际将算法应用到实际问题中。这一笔记我们开始讲学习理论,了解理论知识。
下面开始介绍的第一个学习理论是偏差-方差权衡。
当我们讲线性回归时,我们讨论过一个问题:是使用简单的线性假设 y = θ 0 + θ 1 x y = \theta_0 + \theta_1x y=θ0+θ1x来拟合数据还是用更复杂一点的假设 y = θ 0 + θ 1 x + . . . + θ 5 x 5 y = \theta_0 + \theta_1x + ... + \theta_5x^5 y=θ0+θ1x+...+θ5x5来拟合数据呢?
从最右侧的图中可以看到,用五次多项式来拟合数据并不是一个好的模型。尤其是,即使五次多项式对训练样本做出了很好的预测,但我们把并不期待在不基于原有训练集的基础上该假设会有一个良好的预测效果。换句话说,该假设从训练集中习得的结果对其他训练样本并不具有良好的普适性。
这一假设的泛化误差是预期误差,但不必在训练集中存在。
在上述最左侧和最右侧的图都有泛化误差。然而,两种模型出现的问题不同。如果输入特征与输出变量的关系不是线性的,那么即使我们用线性模型去拟合大量的数据集,线性模型仍然不会成功捕获到数据中的结构。
因此,对于上述的问题,线性模型存在较大的偏差,也就是对数据的欠拟合。
除了偏差,泛化误差还有第二个部分,在模型拟合过程中的方差。尤其是当我们最右侧图中的五次多项式,在数据拟合过程中会存在很大的风险。因为在数据集中会偶然得到比平均房价高的数据样本,也会有比平均房价低的数据样本。为了拟合数据集中这些“有欺骗性”的模式,可能会再次出现较大的泛化误差。在这一过拟合过程中,模型有较大的方差。
而对于偏差与方差我们会找到一种折中的方案(平衡)。如果我们的模型太过简单有很少的参数,那么这个模型可能会有较大的偏差(较小的方差);相反如果模型太过复杂有很多的参数,那么这个模型可能会有较大的方差(但是较小的误差)。
在上述的问题中,用二次函数来拟合数据比前两者要好很多。
接下来我们将要更深入的理解过拟合与欠拟合,或者说高偏差与高方差。之后将会提出一个更为正式的机器学习模型,并且尝试证明这两个问题何时会出现。
首先考虑线性分类 h θ ( x ) = g ( θ T x ) h_\theta(x) =g( \theta^Tx) hθ(x)=g(θTx), g ( z ) = 1 { z ≥ 0 } g(z) = 1\{z \geq 0\} g(z)=1{z≥0},其中 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1}。我们可以将这个模型看作逻辑回归(该模型与逻辑回归非常相似,不同的一点是强制让逻辑回归输出0和1作为类标签)。
所以现在给定一组训练集, S = { ( x ( i ) , y ( i ) ) ; i = 1 , . . . , m } S =\{(x^{(i)},y^{(i)});i = 1,...,m\} S={(x(i),y(i));i=1,...,m},其中包含m个训练样本。假设每个样本之间是独立同分布的,并且服从某个分布 D D D。
为了理解偏差和方差,我们将会使用一个简化的机器学习模型(特别说一下,逻辑回归通过对数似然性来拟合参数)。但为了更深入的理解机器学习算法,我们要定义一个简化版的机器学习的模型。
首先定义一个训练误差/风险:
上述公式的含义很明确:被假设错误分类的训练样本之和/总训练样本数 = 被假设错误分类的训练样本所占比例。
我们将要讲的简化版的机器学习模型被称作ERM(经验风险最小化)。
学习算法的目的是选择参数使得训练误差最小化。我们认为ERM算法是最基础的学习算法。(像逻辑回归也可以看作是ERM的近似算法)
对于上述ERM的目的,与其看作是选择参数来使训练误差最小,不如可以等价看作选择一个函数。所以,接下来我们定义一个假设类 H H H——由所有假设(也可以说是所有线性分类器)构成的集合。
![]()
其中每个假设 h θ ∈ { 0 , 1 } h_\theta \in \{0,1\} hθ∈{0,1}。当你在改变参数时,实际上就是在选择不同的函数。
所以,我们需要重新定义ERM,相对于原来的选取参数使得训练误差最小化,改为从 H H H中选取函数。具体定义等式如下:
解析:为什么要用这样的等价形式来表示ERM呢?原因如下:是对接下来的课程内容的考虑,在更为一般的情况下, H H H可能代表其他类的函数,例如可能是一类由神经网络表示的函数,或者是算法需要的从中选取的其他一类的函数。这些情况下,我们会使用这种形式的ERM的定义。
我们接下来要做的就是:尝试理解ERM是一个合理的算法。那么我们需要怎么证明呢?
首先我们需要明确,我们的目的不是对于训练集合的预测有多么准确(也就是说我们的目的不是训练误差),我们的终极目的是:对于我们之前没有遇到过的训练样本的预测效果(也就是说我们的终极目的是一般误差)。
一般误差的定义是:对于一个新的、由某个分布 D D D生成的训练样本 ( x , y ) (x,y) (x,y),假设对该样本错误分类的概率。
接着,我们证明一些结论来表明ERM是一个合理的算法(因为它能带来较小的一般误差)。
两条引理
为了证明我们学到的这一理论的结论,我们先介绍两条引理。
引理1:联合界引理
让 A 1 , A 2 , . . . , A k A_1,A_2,...,A_k A1,A2,...,Ak代表k个不同的事件(一种概率事件,或者发生,或者不发生),这些事件不一定是独立的, A 1 A_1 A1到 A k A_k Ak之间可能是有关联的,那么有:
引理2:Hoeffding不等式
让 Z 1 , Z 2 , . . . , Z m Z_1,Z_2,...,Z_m Z1,Z2,...,Zm是m个独立同分布的随机变量,它们服从均值为 ϕ \phi ϕ的伯努力分布,这意味着 P ( Z i = 1 ) = ϕ P(Z_i = 1) = \phi P(Zi=1)=ϕ,所有对m个独立同分布的随机变量,其均值为 ϕ ^ = ( 1 / m ) ∑ i = 1 m Z i \hat{\phi} = (1/m) \sum_{i = 1}^m Z_i ϕ^=(1/m)∑i=1mZi,给定 γ > 0 \gamma > 0 γ>0,那么有:
上述不等式的含义是:估计的 ϕ \phi ϕ值与真实的 ϕ \phi ϕ值之间的差异,不会超过不等式右侧这个上界。关于不等式右侧的上界有一个理论:随着m的增长上界指数下降。
介绍过引理之后,我们回到ERM话题。
以逻辑回归为例。接下来我们要讲述ERM的性质,需要考虑有限假设类的情形。
令 H H H为一个包含k个假设的假设类。ERM要做的就是从给定的训练集合中,从这k个函数中选取一个,使得训练误差最小。
我们要证明的是:一般误差和最小误差之间的差值有上界,换句话说,如果训练误差不大,那么我们要证明一般误差也不会太大。
证明策略如下:
-
首先,我们要证明一般误差与训练误差近似 $\hat{\varepsilon} \approx \varepsilon $
-
其次,我们要证明ERM输出的假设的一般误差 ε ( h ^ ) \varepsilon(\hat{h}) ε(h^)存在上界
证明过程如下:
第一步
首先,我们不去考虑所有的假设,先考虑一个固定的假设 h j h_j hj,然后我们定义 Z j = 1 { h i ( x ( j ) ) ≠ y ( j ) } ∈ { 0 , 1 } Z_j = 1\{h_i(x^{(j)}) \neq y^{(j)}\} \in \{0,1\} Zj=1{hi(x(j))=y(j)}∈{0,1},含义是第j个样本是否被错误分类的指示函数的值。我们的训练样本是服从某个分布 D D D中随机生成的,每个样本之间都是独立同分布的。很明显, Z j Z_j Zj只能取0或1的值,这是一个伯努力随机变量,那么有 P ( Z j = 1 ) = h i P(Z_j = 1) = h_i P(Zj=1)=hi,伯努力随机变量的均值应该等于假设 h i h_i hi的一般误差。
h i h_i hi的训练误差等于:
再根据引理2可得:
这个结论证明了:对于给定的假设 h i h_i hi,训练误差将会以很大的概率近似于一般误差。随着m的增长,不等式右侧的上界会随之减小。所以,这说明如果训练集合足够大,那么训练误差和一般误差的差距很大。
为了后续的讲述,令A_i 代表 ∣ ε ( h i ) − ε ^ ∣ > γ |\varepsilon(h_i) -\hat{\varepsilon}| > \gamma ∣ε(hi)−ε^∣>γ,则有 P ( A i ) ≤ 2 e x p ( − 2 γ 2 m ) P(A_i) \leq 2exp(-2\gamma^2m) P(Ai)≤2exp(−2γ2m)。
现在我们希望证明:对于整个假设类 H H H,存在如下不等式:
也可以写成如下不等式:
所以,在不小于不等式右侧的概率的情况下,训练误差与一般误差的差距在 γ \gamma γ以内。这个结果被称之为一致收敛。一致收敛暗示了一个事实:当m很大时,所有的一般误差将同时收敛到训练误差。
接下来让我们看一下一致收敛的其他几个表述形式。上述的不等式表达的是一个概率的上界,当我们固定m和 γ \gamma γ时,一致收敛成立的概率是多少?我们有三个感兴趣的参数,第一个是“概率是多少”,第二个是“数据集合的大小m是多少”,以及“误差阈值 γ \gamma γ是多少”。
那么接下来我们可以研究“给定 γ \gamma γ和表现出很大错误的概率 σ \sigma σ,训练集合m要多大才获得符合 γ \gamma γ和 σ \sigma σ的界?”
假设$\sigma =2kexp(-2\gamma^2m) $,当训练集合m满足如下等式时:
训练误差与一般误差的差异都在 γ \gamma γ以内的概率至少为 1 − σ 1-\sigma 1−σ。这个结果被称为样本复杂度界。(需要注意的是,m与 l o g k log k logk成正比,而 l o g k logk logk作为k的函数增长速度很缓慢,这意味着在假设类中增加很多的假设,而所需的训练样本的数量却不会有太大的提高。)
最后一个研究的是“给定m和 σ \sigma σ不变,求解 γ \gamma γ”。得到的结果是:至少在概率 1 − σ 1-\sigma 1−σ以下,对于假设类中所有的假设,训练误差和一般误差之间的差距满足不等式:
第二步
假设,对于假设类中所有的假设都有 ∣ ε ( h ) − ε ( h ) ^ ∣ ≤ γ |\varepsilon(h) - \hat{\varepsilon(h)}| \leq \gamma ∣ε(h)−ε(h)^∣≤γ,在这样的前提下,我们想看看对于一般误差能够证明出什么结论。
定义如下等式:
![]()
![]()
我们要证明这一结论:
第一个不等式利用了假设 ∣ ε ( h ) − ε ( h ) ^ ∣ ≤ γ |\varepsilon(h) - \hat{\varepsilon(h)}| \leq \gamma ∣ε(h)−ε(h)^∣≤γ,第二个不等式利用了 h ^ \hat{h} h^ 的定义(最小的训练误差比最小的一般误差要小),第三个不等式利用了第一个假设(训练误差与一般误差的差距)。根据这三个步骤我们证明了上述不等式成立。
最后,我们将所有的结论放在一起得出一个定理。
定理
令 H H H为一个有限的假设类,包含k个假设,固定m和 σ \sigma σ之后,至少在 1 − σ 1 - \sigma 1−σ概率以下,有这个结论成立:
那么为了证明这个不等式成立,需要使用之前得出的结论,那么就可知一致性收敛成立。所以如果一致性收敛成立的话,上述不等式一定成立。
这个结果可以很好的量化方差与偏差的平衡。举个例子,假如有一个假设类 H H H,可能这是一个仅包含线性函数的假设类,加入我现在考虑把这个类换成包含更多特征的新的类 H ′ H^{'} H′,可能包含了二次函数的假设。那么所有线性函数构成的假设类 H H H是由二次函数构成的假设类 H ′ H^{'} H′的子集( H ⊆ H ′ H \subseteq H^{'} H⊆H′),我们需要哪些权衡?
权衡是:上述定理中 m i n h ∈ H ε ( h ) min_{h \in H}\varepsilon(h) minh∈Hε(h),这一项的结果会更好,因为具有最小一般误差的二次函数相比最好的线性函数来说,一定具有相同或更小的一般误差。所以假设类的切换导致这一项误差减小,那么相应的第二项(开平方跟那一项)要增大。因为假设k增加,这就是偏差与方差的权衡。如果使用一个更大的假设类,可以找到一个更好的函数,但是不能精确拟合出模型的风险也随之提高。
我们可以这样认为,上述定理中的不等式中 m i n h ∈ H ε ( h ) min_{h \in H}\varepsilon(h) minh∈Hε(h)对应着学习算法中的偏差,也可以认为不等式右侧的第二项对应着学习算法中的方差。
扩展
对于一般误差和训练误差与模型复杂度的关系,随着模型复杂度越高,训练集中的数据拟合的越好,训练误差越小。然而,一般误差会在模型复杂度增高的过程中,先下降然后又上升。 下降的部分是因为数据欠拟合导致一般误差较高,同时伴随着较高的偏差;而上升部分是因为数据过拟合导致的,同时伴随着较高的方差。所以,为了最小化一般误差,就需要选择中间复杂度的模型。
推论
针对之前得到的定理,我们得到一个推论:给定假设类 H H H包含k个假设,给定 σ \sigma σ和 γ \gamma γ,为了保证通过ERM选取的假设的一般误差满足不等式: ε ( h ^ ) ≤ m i n h ∈ H ε ( h ) + 2 γ \varepsilon(\hat{h}) \leq min_{h \in H}\varepsilon(h) + 2\gamma ε(h^)≤minh∈Hε(h)+2γ,为了保证概率至少在 1 − σ 1 - \sigma 1−σ以下,这个结论是成立的,那么m需要满足如下条件: