机器学习笔记9——特征选择

无限假设类 H 的情况

上一章针对包含有限个假设类的情况，我们已经证明了一些有用的理论。但是针对包含无限假设的假设类，我们是否能得出类似的结论？

假设给定一个假设类 H ，存在d个实数参数。因为我们使用电脑代表真实值的话，用双精度浮点数64bits（位）代表一个实数。这意味着在我们的学习算法中，假设我们使用双精度浮点数代表每个实数，那么共有 264d bits（位）。因此，假设类是由最多有 k=264d 个不同的假设构成。

从上一章最后一小节中的引理得知，为了保证 ε(h^)≤ε(h∗)+2γ 不等式成立，那么在 1−σ 的概率以下，有如下等式成立：

因此，训练样本的数量与模型中的参数的个数很有可能呈线性相关。

实际上我们依赖于64bits（位）的浮点数的出的这一结论并不完全令人满意，但是结论大致上是正确的：如果我们继续尝试对训练误差最小化，那么为了让包含d个参数的假设类可以“更好的”学习，我们需要与d个参数个数成线性数量的训练样本。

因为上述的论证并不完全令人满意，所以介绍下面的这个（更正式的）论证，证明过程省略。

Vapnik-Chervonenkis维

给定一个由d个点组成的集合 S={x(i),...,x(d)} ，其中 x(i)∈X ，我们说一个假设类可以分散集合S，如果 H 可以实现集合的任意一种的标记形式（就是可以任意为d个点进行标记）。

如果 H 可以分散集合S,那么对于S中任意一种的标记形式，都可以在假设类中找到一个假设 h 对S中的d个样本进行完美预测。

举个例子来说明一下，假设 H 是一个包含了所有二维现行分类器的假设类，而S是一个包含了三个点的集合：

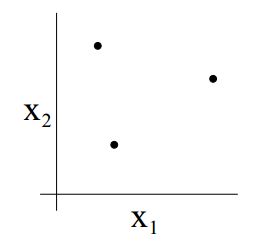
那么对于集合S有八种不同的标记方式：

而对于每一种标记方式，都可以在假设类中找到一个假设对能对这些标记完美的分类。所以根据定义，假设类 H 可以分散集合S。

那么对于更多点的集合S，假设类也能完美的分散吗？答案是不能。篇幅原因不给出证明过程，但直接给出结果：在二维的情况下，任意的现行分类器都不能分离四个点构成的集合。

下面我们介绍一下VC维的定义。给定一个假设类 H ，其VC维表示为 VC(H) ，表示能被 H 分散的最大集合的大小（如果 H 可以分散任意大小的集合，那么它的 VC(H) 无穷大）。

举个例子，如果 H 是所有二维分类器构成的假设类，那么它的VC维应为3。因为之前我们看到任意二维分类中的四个点的集合都不能被分离。

当然也不是所有的三个点的集合都能被分离，比如下面这中情况就无法分离：

但是这种情况是没有问题的，只要存在大小为3的集合可以被分散，那么VC维就等于3。但是绝对不可能等于4。

上述的理论可以推广到一般情况，对于任意维度，由n维线性分类器构成的假设类，那么它的VC维等于（n+1）。

那么由上述结论可得出定理：

给定假设类 H ，让它的 VC(H)=d ，那么至少在 1−σ 的概率下，针对假设类中所有的假设，有下面的结论成立：

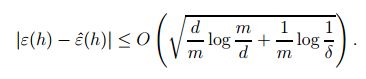
因此，在至少在 1−σ 的概率下，同样可得：

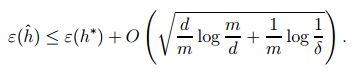
可将上述的公式写作如下的引理。

引理：为了保证 ε(h^)≤ε(h∗)+2γ 这个结论在 1−σ 概率下成立，应该满足以下结论： m=Oγ,σ(d) ，m与 Oγ,σ(d) 呈线性关系。

这表明样本复杂度的上界由VC维决定。实际上，在大多数合理的假设类中，VC维与模型的参数数量成正比。所以也可以得出训练样本的数量与模型的参数的数量成线性关系。

模型选择

模型选择提供了一类方法可以自动在偏差和方差之间权衡。

一些模型选择的例子可能包括：1. θ0+θ1x , θ0+θ1x+θ2x2 ，….., θ0+θ1x+...+θ10x10 等等，本质上就是选择多项式的次数；2.在局部加权线性回归/其他加权中选择带宽函数；3.还包括在支持向量机中选择参数C（参数C控制了一种权衡关系：你希望你的样本会以多大的间隔被分隔？对于那些错误分类的样本惩罚力度是多少？）。

接下来会提出一个自动选择模型的方法。

假设有一个包含有限个模型的集合，表示为 H={M1,M2,M3...} ，集合中可以包括多项式函数，也可以包括带宽函数等，可以将集合中的函数离散成不同的值，然后选择一个具体的值。

那么如何选择一个合适的值呢？其实有很多中标准的方法。

其中一种称作保留交叉验证。给定一个训练集合，随机划分成两个子集。一个称之为训练子集，一个称之为保留交叉验证子集。训练子集用来训练模型，而保留交叉验证自己用来进行测试。最后选择具有最小测试误差的模型作为结果。

通常情况下70%的数据训练模型，剩下的30%进行交叉验证。最后还可以用100%的数据对选出的模型进行重新训练。

这一方法存在一个缺点：现实生活中训练数据很难获得，拿出30%的数据做模型选择不太实际。

那么接下来介绍几种保留交叉验证的变化方法，可以更高效的利用数据。

• k重交叉验证
  算法思路如下：将数据划分成k份（k = 10比较常见），然后利用k - 1个部分进行训练，用剩下的一个部分做测试；最后对这k个误差求平均，得到这个模型的一般误差的估计。
  缺点：计算量大，为了验证模型需要训练k次。

• 留1交叉验证
  算法思路如下：将数据划分成k份（k = 训练样本的数量m），留出一个样本，剩下的进行训练。对数据的利用效率比k重交叉验证要高，但计算量也会相应增多。所以，这种方法需要在样本数量很少的情况下使用。

关于模型选择还有一种特例：特征选择问题。举个例子，对于很多机器学习的算法来说，可能面对一个非常高维的特征空间，即输入特征x的维数可能非常高。那么这么多的特征如果都用上可能会存在过拟合的风险。那么如果能减少特征的数量，就可以减少算法的方差。

所以，在特征选择问题中，我们会从原始的特征中选出一个子集，我们认为这个子集对特定的学习问题来说是最为相关的，这样就拥有了一个更为简单的假设类。

那么应该如何进行特征选择呢？对于n个特征，会有 2n 个子集，在进行选取的过程中，可以使用不同的启发式规则进行搜索。如果用简单的搜索方式在 2n 个子集中搜索，那么空间太大，我们不可能对每一种可能的子集进行枚举。

接下来提出几个搜索方法，用于便捷的进行特征选择：

1.前向选择算法

算法流程如下：

• 初始化特征子集 F=空

• 重复如下过程{

  (1) for i = 1,…n 尝试将特征i将入到 F 中，并对模型进行交叉验证

  (2) 令 F=F∪ (1)中找到的最好的特征
  }

• 输出得到的最好的假设

2.后向选择算法

算法流程如下：

• 初始化特征集 F={1,2,...n}

• 之后每次从 F 中删除一个特征（与前向选择算法一样，此处需要循环处理）

• 输出得到的最好的假设

因为后向选择算法中初始特征集合包含所有的特征，如果特征维数很高，那么一开始用这个特征集合进行训练模型可能不妥。所以前向选择算法用的更多一些。

（前向与后向选择算法可以统称为封装特征选择算法。这种算法效果通常很好，比接下来要讲的这一类选择算法通常要好一些。但是这一封装算法需要很大的计算量。）

3.过滤特征选择算法

算法基本思想如下：对于每一个特征i，我们都要计算一些衡量标准，来衡量对y的影响有多大。可以通过计算与y的相关度来衡量，然后选择与y相关度最高的k个特征；另一种方式是，计算特征x与y的相互信息，用 MI(xi，y) 来代替，有如下等式：

等式中所有的概率分布都可以用训练数据进行估计。等式同样可以这样表示：

其中KL距离用来度量不同的概率分布之间的差异。换句话说，KL距离是一种关于两个概率分布之间差异的一种度量标准。 P(xi,y) 代表两个变量 x,y 之间的joint概率分布。如果x，y相互独立，那么这两个概率相等，分布相同，KL距离为0；相反，如果x，y之间的依赖性很高，换句话说，如果x对y的值影响很大，那么KL距离将会很大。

之后，选择前k个特征。对特征验证的话可以选择交叉特征验证算法。