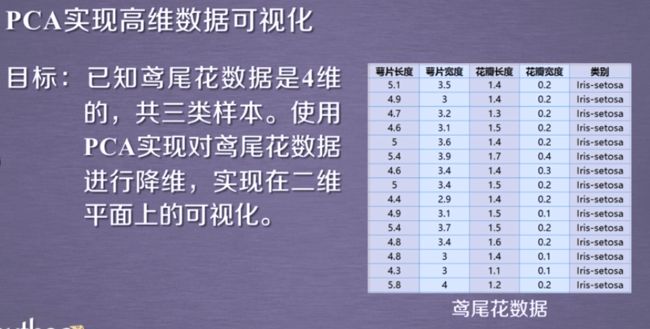
慕课学习笔记——1机器学习（无监督学习）

无监督学习
1. 导学部分

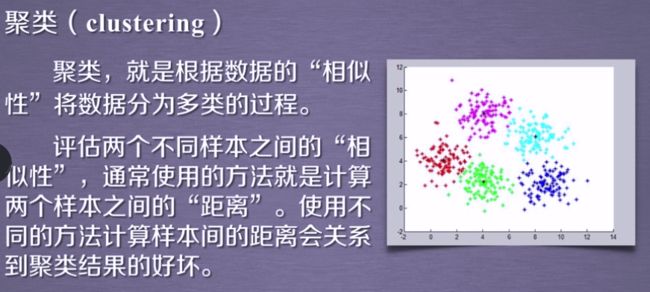**tips：**使用聚类要计算距离



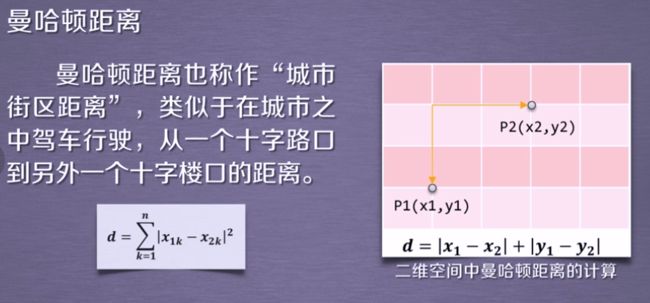
tips：使用马氏距离，中心到红点的距离大于中心到绿点的距离（这里不太明白）



**tips：**使用了三种算法：dbscan函数（最快）；近邻传播算法（最慢）；谱聚类算法

常用聚类算法

降维
用于提高运算性能



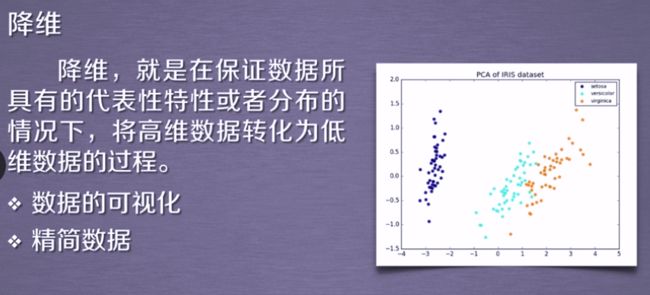
常用降维算法


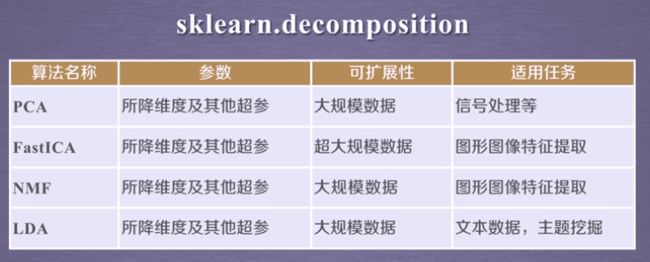
**思考：**上述问题哪些是聚类，哪些是降维问题？
降维：4
聚类：123

2. 聚类算法
2.1 K-means算法


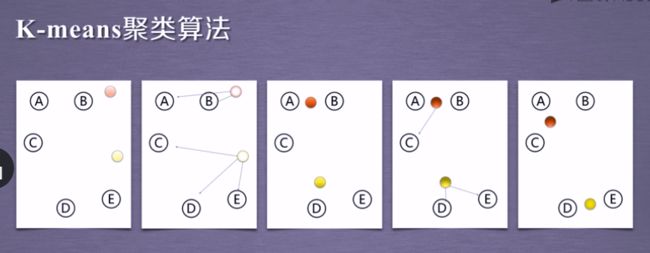
**Tips：**选取距离各点最近的中心点，由此分为两组，反复评估中心距离各点的距离












聚成4类时明显可以看到消费层级分得比较好了



自己练习的代码

#了解1999年各个省份的消费水平在国内的情况
#Kmeans算法-具体可以通过help（Kmeans）手册查询

import numpy as np 
from sklearn.cluster import KMeans

#一个获取数据的函数
def loadData(filePath):
    #r+读写模式
    fr = open(filePath,'r+')   
    #一次读取全文
    lines = fr.readlines()     
    retData = []     
    retCityName = []   
    #for循环内部用于处理单行数据，循环次数lines(31)次
    for line in lines:  
        #删除作为间隔的逗号
        items = line.strip().split(",") 
        #用于储存城市名称，位于第一列        
        retCityName.append(items[0]) 
        #用于储存城市的各项消费信息
        #for循环单行内的每个元素
        #[float(items[i])这是什么意思？        
        retData.append([float(items[i]) for i in range(1,len(items))])     
    return retData,retCityName 
     
if __name__ == '__main__': 
    #载入数据 
    #loadData是上面创建的函数
    #因为是二维列表，所以赋值符前需要有两个变量与之对应
    #但是这两个变量的放置顺序不太明白——与函数部分的返回值相对应
    data,cityName = loadData('D:/lolita/Machine learning/city.txt')     
    #创建实例，分成4类
    km = KMeans(n_clusters=4) 
    #调用Kmeans()算法 fit_predict()方法计算 
    # fit_predict表示拟合+预测，也可以分开写
    #label作为聚类后各数据所属的标签
    label = km.fit_predict(data) 
    #计算各个类别的聚类中心值，然后求和
    expenses = np.sum(km.cluster_centers_,axis=1)     
    
    #城市聚类是个二维列表
    #将城市按label分成4簇
    CityCluster = [[],[],[],[]]
    #循环次数为cityname的长度,在ipython中调试后发现长度为31,数据有31行
    #31是由于有31行1维数据     
    for i in range(len(cityName)):
         # 将每个簇的城市输出
         #这句还是不太明白
         CityCluster[label[i]].append(cityName[i])
    #循环citycluster列表的长度，即4
    for i in range(len(CityCluster)):  
        #打印每个簇的平均花费输出，保留两位小数
        print("Expenses:%.2f" % expenses[i])
        #打印分好的类         
        print(CityCluster[i])

2.2 DBSCAN方法及应用













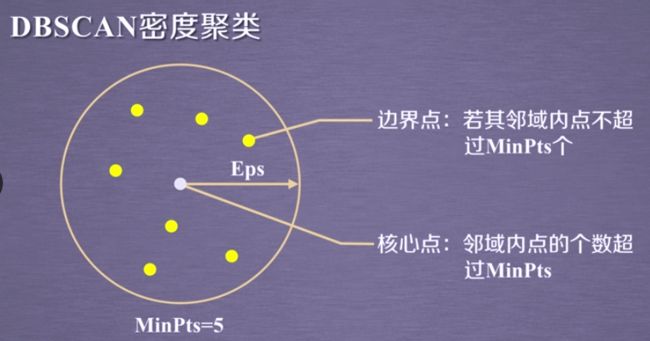
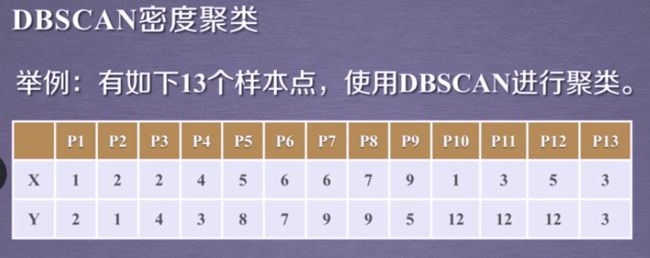
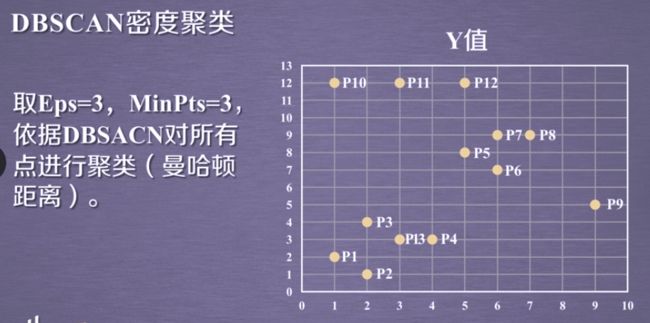
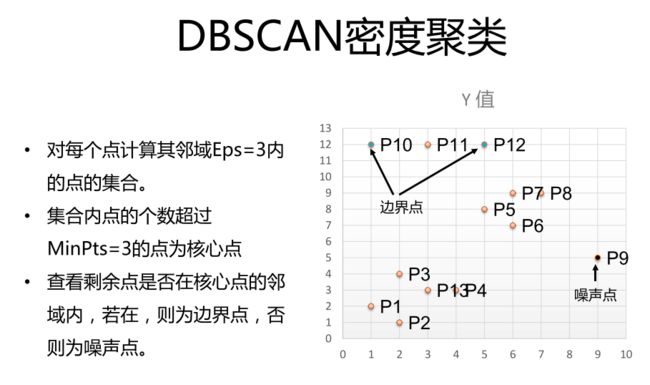
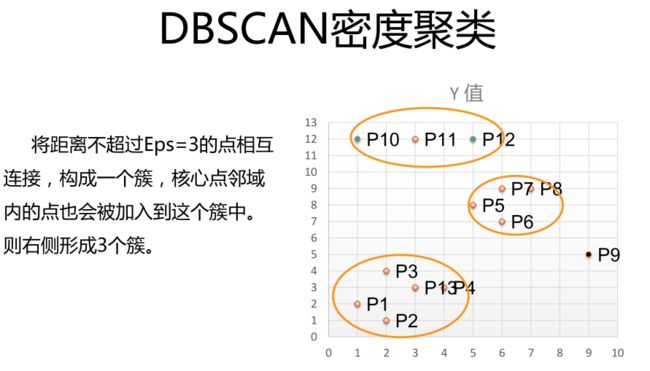
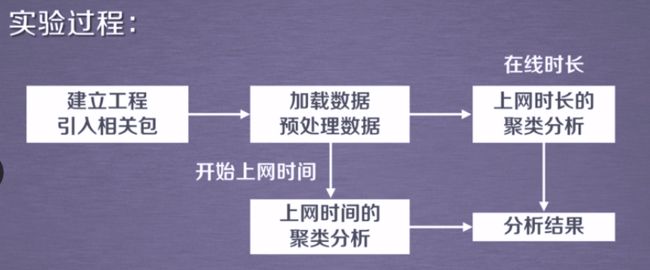
metric默认为曼哈顿距离

##聚类2——DBSCAN
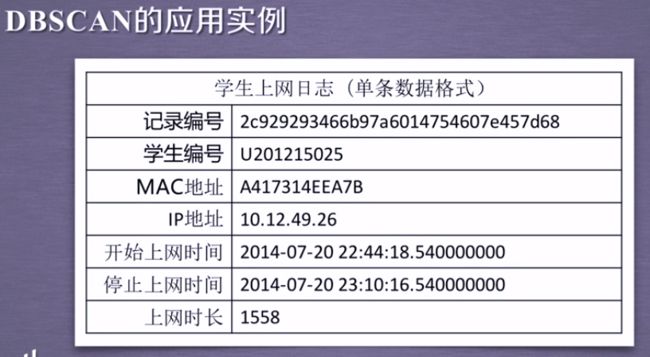
#分析学生开始上网和上网时长的模式
#单个学生上网日志（记录编号，学生编号，MAC地址，IP地址，开始，停止上网时间，上网时长）
#1.建立工程，引入sklearn相关包
import numpy as np 
import sklearn.cluster as skc 
from sklearn import metrics 
import matplotlib.pyplot as plt 

#2.加载数据，预处理数据
#读取每条数据中的mac地址，开始上网时间，上网时长

#mac2id是一个字典
#key是mac地址，value是对应mac地址的上网时长以及开始上网时间    
mac2id=dict() #字典
onlinetimes=[] #列表，作为字典的值

#数据的形式是utf-8编码的，但处理的默认字符编码是其他格式
f=open('D:/lolita/Machine learning/TestData.txt',encoding='utf-8') 
for line in f:  
    """读取每条数据中的mac地址，开始上网时间，上网时长"""
    #读取以逗号分隔的单行数据的第三个(在ipython中可以调试出该行代码功能)
    mac=line.split(',')[2]     
    #读取上网时长并转化为整数
    onlinetime=int(line.split(',')[6]) 
    #读取开始时间(24小时制)    
    starttime=int(line.split(',')[4].split(' ')[1].split(':')[0]) 
    
    if mac not in mac2id:
        #mac2id字典中键为mac地址，值为对应mac地址的开始上网时间和上网时长         
        mac2id[mac]=len(onlinetimes)#一个循环增加一个键共289个
        onlinetimes.append((starttime,onlinetime)) #一个键对应对应列表中两个值    
    else:
        "else后面这样表示是什么意思？"         
        onlinetimes[mac2id[mac]]=[(starttime,onlinetime)]
        
#开始上网时间聚类，创建DBSCAN，进行训练，获得标签
#将数据变换成n行2列的数组
real_X=np.array(onlinetimes).reshape((-1,2)) 
#读取n行第一列数据,0:1
"为什么不能直接写成1，不是直接读取第1列的意思吗？可能是字典的原因？"
X=real_X[:,0:1] 
#eps-以核心点为中心，0.01为半径的一个范围确定这个簇
#min_samples-一个簇包含20个点
#所以需要数学功底的部分就在于如何去确定这个半径和范围内的点
#默认欧式距离,但是使用曼哈顿距离计算结果一致
db=skc.DBSCAN(eps=0.01,min_samples=20).fit(X) 
#labels为每个数据的簇标签
labels = db.labels_ 
"打印数据被记上的标签（划分标准是什么？）"
print('Labels:') 
print(labels) #共289个
#计算标签为-1，即噪声数据的比例
raito=len(labels[labels[:] == -1]) / len(labels) 
print('Noise raito:',format(raito, '.2%')) 
#计算簇的个数并打印，评价聚类效果
#先把labels变为集合，集合无重复，计算总label个数，减去噪声label；即0-5共6个簇
#直接减1也可
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) 
print('Estimated number of clusters: %d' % n_clusters_) 
#轮廓系数（Silhouette Coefficient）的值是介于 [-1,1] 
#越趋近于1代表内聚度和分离度都相对较优
print("Silhouette Coefficient: %0.3f"% metrics.silhouette_score(X, 
       labels)) 
#打印各簇标号以及各簇内数据
for i in range(n_clusters_):     
    print('Cluster ',i,':') 
    #array.flatten()为折叠成一维数组
    print(list(X[labels == i].flatten()))
    
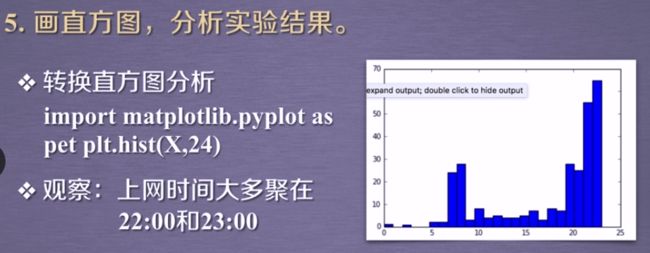
#绘制直方图
#第一个参数是arr，需要计算直方图的一维数组
#第二个参数是bins，决定了每个直方块的宽度
#plt.hist(X,24)
plt.subplot(121)
plt.hist(X,24)
plt.xlabel('上网时间')#注意中文字体格式
plt.ylabel('上网时长')
plt.axis([0,25,0,70])

#2.2上网时长聚类，创建DBSCAN，进行训练，获得标签
Y=np.log(1+real_X[:,1:])
db=skc.DBSCAN(eps=0.14,min_samples=10).fit(Y)
labels=db.labels_
print('Labels_Y:%s'%labels)
ratio=len(labels[labels[:]==-1])/len(labels)
print('Noise ratio:{:.2%}'.format(ratio))
n_clusters_=len(set(labels))-(1 if -1 in labels else 0)
print('Estimated number of cluster:%d'%n_clusters_)
print('Silhouette Coefficient:%0.3f'%metrics.silhouette_score(Y,labels))
#统计每一个簇内的样本个数，均值，标准差
for i in range(n_clusters_):
    print('Cluster',i,':')
    count=len(Y[labels==i])
    mean=np.mean(real_X[labels==i][:,1])
    std=np.std(real_X[labels==i][:,1])
    print('\t number of sample:%d'%count)
    print('\t mean of sample  :%.2f'%mean)
    print('\t std of sample   :{:.2f}'.format(std))
plt.subplot(122)
plt.subplots_adjust(wspace=0.3)#调整subplots之间横向间距，纵向用hspace
x=np.linspace(0,len(labels),len(labels))
plt.plot(x,real_X[:,1]) 

转换之前数据不适合聚类分析，进行聚类转换【为什么呢？太局限了吧】

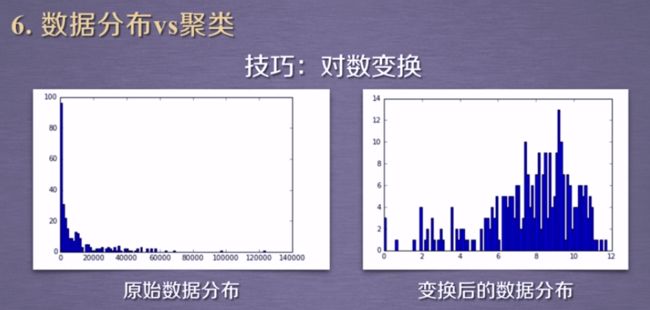
另一种方式进行聚类



3. 降维算法
3.1 PCA算法（主成分分析）

主成分分析前需要回顾相关术语

• 方差
• 协方差
• 协方差矩阵
• 特征向量和特征值
  
  
  
  
  具详细推导见西瓜书
  
  四维数据鸢尾花
  

#降维算法
#3.1PCA算法 
#给四维数据鸢尾花降维
"""以鸢尾花的特征作为数据，共有数据集包含150个数据集，
分为3类setosa(山鸢尾), versicolor(变色鸢尾), virginica(维吉尼亚鸢尾)
每类50个数据，每条数据包含4个属性数据 和 一个类别数据."""

import matplotlib.pyplot as plt 
#降维库
from sklearn.decomposition import PCA 
from sklearn.datasets import load_iris 

#加载数据
data = load_iris() 
#以y表示数据集中的标签，以x表示数据集中的属性数据
y = data.target #字典的键key
X = data.data #值value,四维
#加载PCA算法，设置维度
pca = PCA(n_components=2) 
#对原始数据进行降维，保存在reduced_X中
reduced_X = pca.fit_transform(X) 
#三类数据点：setosa(山鸢尾), versicolor(变色鸢尾), virginica(维吉尼亚鸢尾)
red_x, red_y = [], [] 
blue_x, blue_y = [], [] 
green_x, green_y = [], [] 

#按照鸢尾花的类别将降维后的数据点保存在不同的列表中
for i in range(len(reduced_X)):     
    if y[i] == 0:         
        red_x.append(reduced_X[i][0])         
        red_y.append(reduced_X[i][1])     
    elif y[i] == 1:         
        blue_x.append(reduced_X[i][0])         
        blue_y.append(reduced_X[i][1])     
    else:         
        green_x.append(reduced_X[i][0])         
        green_y.append(reduced_X[i][1]) 

#绘制散点图_三类数据
plt.scatter(red_x, red_y, c='r', marker='x') 
plt.scatter(blue_x, blue_y, c='b', marker='D') 
plt.scatter(green_x, green_y, c='g', marker='.') 
plt.show()

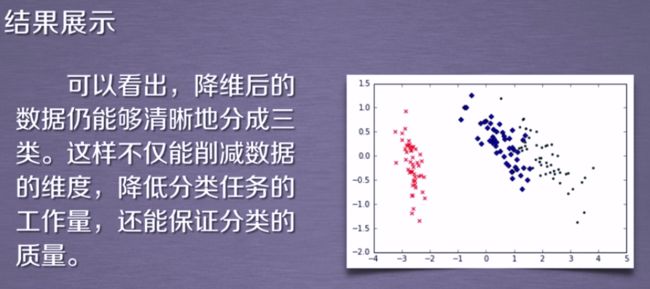
3.2 降维之NMF算法





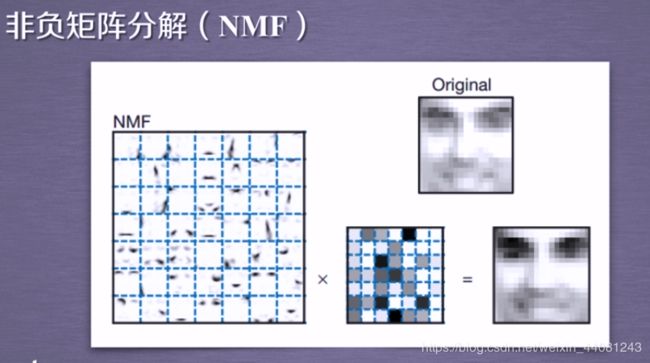
至于W和H矩阵的具体求解方法，其实质是迭代算法，参考链接

#降维算法
#NMF算法_非负矩阵分解
import matplotlib.pyplot as plt
from sklearn import decomposition
#加载Olivetti人脸数据集导入函数
from sklearn.datasets import fetch_olivetti_faces
#加载RandomState用于创建随机种子
from numpy.random import RandomState

#设置基本参数并加载数据
#设置图像展示时的排列数据
n_row, n_col = 2, 3 
#设置提取特征的数目
n_components = n_row * n_col 
#设置人脸数据图片的大小
image_shape = (64, 64)
#加载数据并打乱顺序_shuffle打乱
"randomatate的含义是？"
dataset = fetch_olivetti_faces(shuffle=True, random_state=RandomState(0)) 
faces = dataset.data 

#设置图像展示方式
def plot_gallery(title, images, n_col=n_col, n_row=n_row): 
    #创建图片，并指定图片大小（英寸）    
    "2.是？想表示浮点数？是的"
    plt.figure(figsize=(2. * n_col, 2.26 * n_row)) 
    #设置标题及字号大小     
    plt.suptitle(title, size=16)  
    #enumerate_枚举法循环,同时遍历索引和元素
    for i, comp in enumerate(images):         
        #选择画制的子图
        plt.subplot(n_row, n_col, i + 1)         
        vmax = max(comp.max(), -comp.min())
        
        #对数值归一化，并以灰度图形式显示
        "代码内部是什么意思？"
        plt.imshow(comp.reshape(image_shape), cmap=plt.cm.gray,                    
                   interpolation='nearest', 
                   vmin=-vmax, vmax=vmax)   
        #去除子图的坐标轴标签
        plt.xticks(())         
        plt.yticks(())     
    #对子图位置及间隔调整
    plt.subplots_adjust(0.01, 0.05, 0.99, 0.94, 0.04, 0.)      
#    plot_gallery("First centered Olivetti faces", faces[:n_components])可以不要吧

#创建特征提取的对象NMF，使用PCA进行对比
#NMF和PCA实例——将它们放在同一个列表中
estimators = [     ('Eigenfaces - PCA using randomized SVD',     
                    decomposition.PCA(n_components=6,whiten=True)),     
    ('Non-negative components - NMF',          
     decomposition.NMF(n_components=6, init='nndsvda', 
                       tol=5e-3)) ] 
    
#降维后数据点可视化
#分别调用PCA和NMF
for name, estimator in estimators:     
#    print("Extracting the top %d %s..." % (n_components, name))     
#    print(faces.shape)     可以不要
    
    #调用PCA或NMF提取特征
    estimator.fit(faces)
    #获取提取的特征     
    components_ = estimator.components_
    #按照固定格式进行排列——plot_gallery是个函数
    plot_gallery(name, components_[:n_components]) 
    
plt.show()

#可以不要的那几行代码，加上貌似会进入死循环

4.基于聚类的图像分割——Kmeans算法