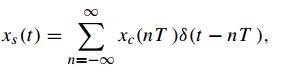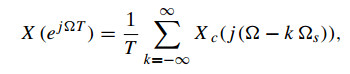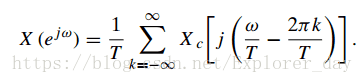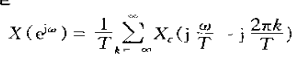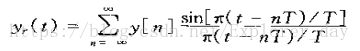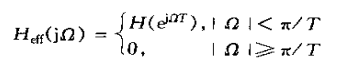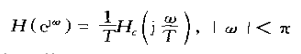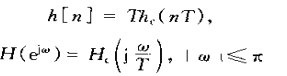《离散时间信号处理学习笔记》—连续时间信号的采样(一)
注:本博客是基于奥本海姆《离散时间信号处理》第三版编写,主要是为了自己学习的复习与加深。
一、周期采样
1、信号的离散表示可以由多种形式,包括各种类型的基展开,信号建模的参数模型和非均匀采样。这些各种类型的表示方法通常都始于通过周期采样得到的联系时间信号的离散时间表示,吉言本·序列x[n]是按照如下关系由连续时间信号xc(t)得到的:
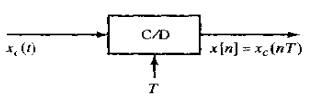
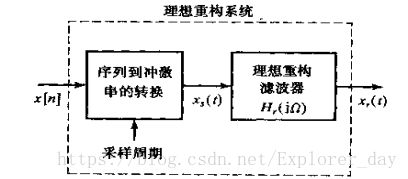
其中,T为采样周期,而它的导数fx=1/T为采样频率,即每秒内的样本数。当要想用护肤/秒(rad/s)的频率时,也将采样频率表示为![]() 把实现式(4.1)所描述的系统称为理想连续时间到离散时间(C/D)转换器,如下图所示,
把实现式(4.1)所描述的系统称为理想连续时间到离散时间(C/D)转换器,如下图所示,
2、采样一般是不可逆的,也就是说,已知输出x[n],一般不可能恢复xc(t),即采样器的输入。在数学上以两步来表示采样过程是方便的。它由一个冲激串调制器紧跟着一个由冲激串到序列的转换来构成。周期冲激串为
式中,![]() 是单位冲激函数。s(t)和xc(t)的乘积为
是单位冲激函数。s(t)和xc(t)的乘积为
利用连续时间冲激函数的帅选性质,xs(t)可表示为
也就是说,在采样时刻nT处的冲激大小(面积)等于连续时间信号在那一刻的值。
3、xs(t)和x[n]之间的本质区别在于:在某种意义上,xs(t)还是一个连续时间信号(具体为一个冲激串),它除了在整数倍的时刻以外都为零;另一面。序列x[n]是以整数变量n给出的,事实上这就引入了时间归一化过程,叶即数的序列x[n]已没有任何明显的有关采样率的信息。再者,xc(t)的样本在x[n]中是用有限数值来表示的,而不是在xs(t)中以冲激面积来表示的。
二、采样的频域表示
1、奈奎斯特采样定理:
令xc(t)是一个带限信号,
那么xc(t)能唯一地由它的样本![]() 所决定的,唯有
所决定的,唯有
频率![]() 一般称为奈奎斯特频率,而频率2
一般称为奈奎斯特频率,而频率2![]() 称为奈奎斯特率。
称为奈奎斯特率。
2、x[n]的离散时间博里叶变换使用![]() 和
和![]() 来表示以及
来表示以及![]() :的另一种表达式
:的另一种表达式
或者等效为
三、由样本重构带限信号
1、根据采样定理,如果已给出一个样本序列x[n],就能形成一个冲激串xs(t),在xs(t)中令相继的冲激面积等于相继的个序列值,既有
第n个样本值与在t-nT时的冲激有关,其中,T是与序列x[n]有关的采样周期。如果将这个冲激串输入到频率响应为![]() 和冲激响应为hr(t)的理想低通连续时间滤波器,那么滤波器的输出即为
和冲激响应为hr(t)的理想低通连续时间滤波器,那么滤波器的输出即为
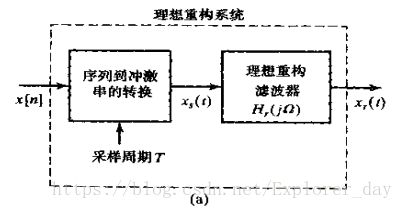
这样一个信号重构的方框图如下图所示
该理想重构滤波器的增益为T,截止频率为![]() 。下图表示了理想重构滤波器的频率响应。
。下图表示了理想重构滤波器的频率响应。
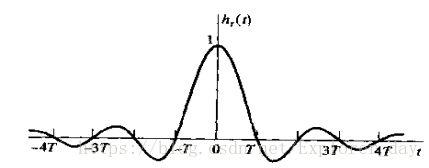
对于截止频率为π/T时相应的冲激响应hr(t)就是![]() 的博里叶变换,由下式给出
的博里叶变换,由下式给出
冲激响应如下图所示
将式(4.10)带入式(4.9)可得
式(4.9)和式(4.10)将连续时间信号表示成基函数hr(t-nT)的线性组合,样本x[n]作为其系数。对基函数和响应系数的不同选取便得到了不同类型的连续时间函数。
2、定义一个从样本序列重构一个带限信号的理想系统,并将该系统称为理想离散到连续时间(D/C)转换器。如下图所示
该理想D/C转换器的性质最容易在频域中看出。为了导出在频域的输入/输出关系,考虑式(4.9)或式(4.10)的博里叶变换,即
由于![]() 对于所有求和公式是公共的,上式可写成
对于所有求和公式是公共的,上式可写成
式(4.13)给出了该理想D/C转换器的频域描述。
四、连续时间信号的离散时间处理
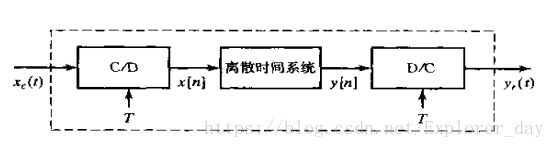
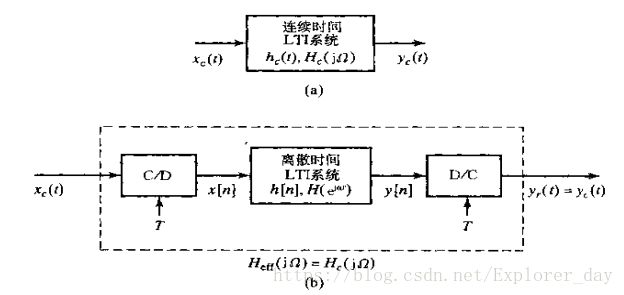
1、离散时间系统的主要应用于连续时间信号的处理。这可以用下图来表示
的一般形式的系统来完成。该系统是由一个C/D转换器紧跟着一个离散时间系统,再跟着一个D/C转换器的级联所构成的。
1)C/D转换器产生一个离散时间信号如下;
![]() 式(4.14)
式(4.14)
这就是连续时间信号xc(t)的样本序列。这个序列的离散时间博里叶变换与连续时间输入信号的博里叶变换的关系为
2)、D/C转换器产生一个如下式的连续时间输入信号;
这里序列y[n的离散时间系统当输入为x[n]时的输出。由式(4.13)可知,yr(t)的连续时间博里叶变换![]() 和y[n]的离散时间博里叶变换
和y[n]的离散时间博里叶变换![]() 的关系如下式;
的关系如下式;
接下来,把输出序列y[n]和输入序列x[n],或者等效为把![]() 和
和![]() 联系起来。
联系起来。
一)、连续时间信号的离散时间LTI处理
1、如果上图中的离散时间时间系统是线性和时不变的,那么就有
![]() 式(4.18)
式(4.18)
这里,![]() 是该系统的频率响应,或者说是单位脉冲响应的博里叶变换,而
是该系统的频率响应,或者说是单位脉冲响应的博里叶变换,而![]() 和
和![]() 则分别作为输入和输出的博里叶变换。将式(4.17)和式(4.18)接合起来,就可以得到
则分别作为输入和输出的博里叶变换。将式(4.17)和式(4.18)接合起来,就可以得到
![]() 式(4.19)
式(4.19)
接下来,利用式(4.15),并且![]() ,有
,有
如果![]() 那么理想低通重构滤波器
那么理想低通重构滤波器![]() 抵消了1/T因子,并且仅选择式(4.20)中k=0这一项,则
抵消了1/T因子,并且仅选择式(4.20)中k=0这一项,则
因此,如果![]() 是带限的,并且采样率高于奈奎斯特率,那么输出与输入就通过夏素关系联系起来;
是带限的,并且采样率高于奈奎斯特率,那么输出与输入就通过夏素关系联系起来;
式中
也就是说,整个连续时间系统等效于一个线性时不变系统,其有效频率响应由式(4.23)给出.。
2、图中所示系统的线性和时不变性特性依赖于两个因素;
1)、第一,离散时间系统必须是线性和是不变的。
2)、第二,输入信号必须是带限的,并且采样率要足够高,以使得任何混叠部分都被离散时间系统所消除。
二)、脉冲响应不变
1、鉴定已经给出所要求的的连续时间系统,希望如上面所讨论的实现它,如下图所示
由于![]() 是带限的,式(4.23)给出了如何选择
是带限的,式(4.23)给出了如何选择![]() ,以满足
,以满足![]() 特别是
特别是
进一步的要求是选择T,使得
在式(4.24)和式(4.25)的约束下,连续时间冲激响应hc(t)和离散时间单位脉冲响应h[n]之间也存在一个直接而有用的关系。特别是下面将要证明的,存在有
![]() 式(4.26)
式(4.26)
即,离散时间系统的单位脉冲响应就是一个在幅度上受到加权hc(t)的采样序列。当h[n]和hc(t)通过式(4.26)联系在一起时,该离散时间系统就可以说成是连续时间系统的一个脉冲响应不变形式。
2、在下式
中,将x[n]和xc(t)分别用h[n]和hc(t)代替,即
下式
就变为
或者式(4.25)成立
考虑到式(4.26)中的幅度因子T,将式(4.28)和式(4.30)做一点变化,就得到