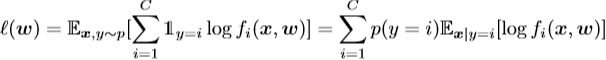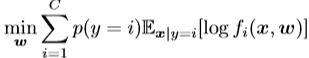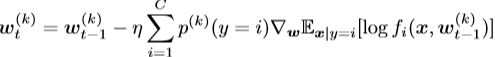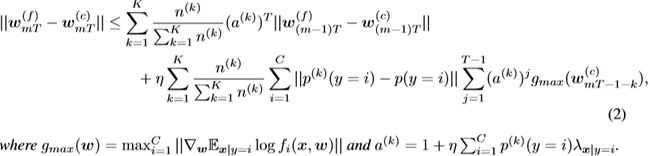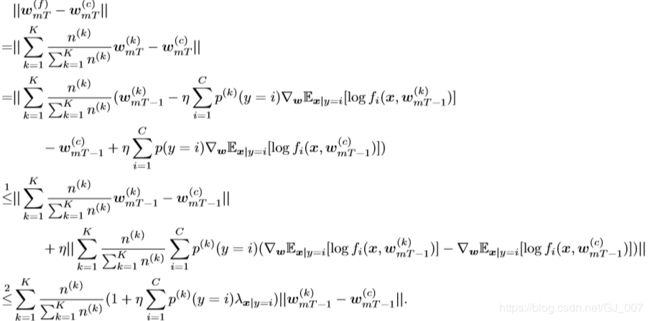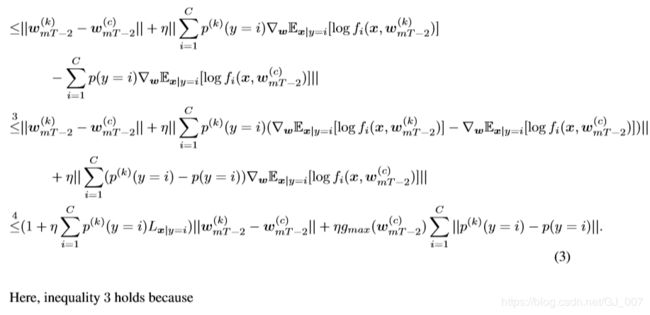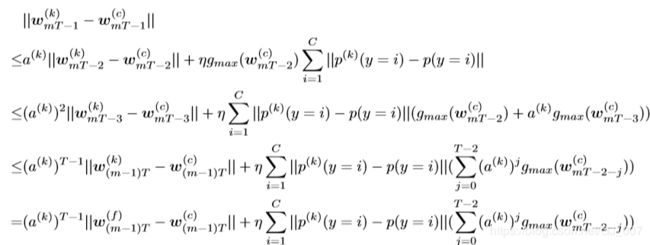Federated Learning with Non-IID Data

Federated Learning with Non-IID Data

论文中分析了FedAvg算法在Non-IID数据时，准确率下降的原因。并提出共享5%的数据可提高准确率。

论文笔记参考：https://blog.csdn.net/GJ_007/article/details/104768415

Federated Learning with Non-IID Data

Abstract

联邦学习支持边缘受限的计算设备（例如移动电话和物联网设备）在保持训练本地数据的同时共享模型。用去中心化的方法训练模型保障了隐私、安全、可管理和经济效益。在这项工作中，我们关注的是当本地数据为non-IID时联邦学习的统计挑战。我们首先展示了联邦学习的准确性显著降低，在为高度倾斜的non-IID数据训练的神经网络中，联邦学习的准确性降低了大约55%，在这种情况下，每个客户端设备只训练一类数据。我们进一步证明，这种精度下降可以用weight divergence来解释，weight divergence可以用每个设备上的类分布和种群分布之间的搬土距离(earth mover’s distance EMD)来量化（参考https://blog.csdn.net/GJ_007/article/details/104632863）。为了解决这个问题，我们提出了一个策略来提高在non-IID数据上的训练，通过创建一个可以在所有边缘设备上全局共享的数据子集。实验表明，仅使用5%的全局共享数据，CIFAR-10数据集的准确性可提高约30%。

1 Introduction

移动设备已成为全球数十亿用户的主要计算资源，并且在未来几年内，还将有数十亿物联网设备上线。这些设备产生了大量有价值的数据，使用这些数据训练的机器学习模型有潜力提高许多应用程序的智能性。但是，要在移动设备上启用这些特性，通常需要在服务器上共享全局数据，以便训练出令人满意的模型。从隐私、安全、可管理或经济角度来看，这可能是不可能或不可取的。因此，将数据保存在本地的同时还可以共享模型的方法越来越有吸引力。

近年来，在设备推理方面取得了很大的进展[1,2]。联邦学习[3,4,5]也提供了在本地进行培训的方法。McMahan等人[3]引入了Federated Averaging（FedAvg）算法，并证明了FedAvg在基准图像分类数据集（例如MNIST [6]和CIFAR-10 [7]）上训练卷积神经网络（CNN）以及在语言数据集上训练LSTM的鲁棒性[8]。

最近有很多关于解决联邦学习的交流挑战的研究。，如何降低传输深度网络的巨大权值矩阵的通信成本，以及由于网络连接、功率和计算约束而导致的意外中断或同步延迟。Bonawitz[9]等人开发了一种用于联邦学习的高效安全聚合协议，允许服务器执行来自移动设备的高维数据的计算。Koneˇcn` y等人[10]提出了结构化的更新和sketched updates,降低通信成本由两个数量级。Lin等人[11]提出了深度梯度压缩(Deep Gradient Compression, DGC)，将通信带宽降低两个数量级，以训练高质量的模型。

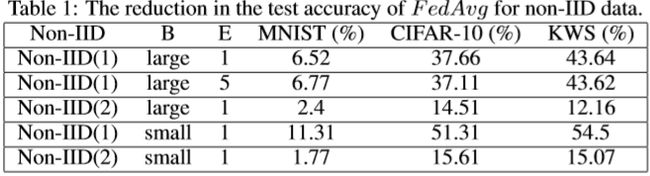
除了通信方面的挑战，联邦学习还面临着统计方面的挑战。联邦学习依赖于随机梯度下降法(SGD)，该方法被广泛用于训练具有良好经验性能的深度网络[12,13,14,15,16,17]。训练数据的IID抽样对于确保随机梯度是全梯度的无偏估计非常重要[15,16,18]。在实践中，假设每个边缘设备上的本地数据总是IID是不现实的。为了解决non-IID挑战，Smith[28]等人提出了一个多任务学习(MTL)框架，并开发了MOCHA来解决MTL中的系统挑战。但是这种方法与以前关于联邦学习的工作有很大的不同。McMahan等人[3]已经证明FedAvg可以处理某些non-IID数据。然而，正如我们将在第2节中展示的，在non-IID数据高度倾斜的情况下，使用FedAvg算法训练的卷积神经网络的精度可以显著降低，对于MNIST数据集高达11% 、对于CIFAR-10数据集达51% 、keyword spotting(KWS)数据集达55%。

了解决联邦学习的这种统计挑战，我们在第3节中展示了准确性下降可以归因于weight divergence，它量化了具有相同权值初始化的两个不同训练过程的weight divergence。然后，我们证明了训练中的权值分歧是由每个设备(或客户端)上的类分布与总体分布之间的搬土距离(EMD)所限定的。这个边界受到学习速率、同步步骤和梯度的影响。最后在第四部分，我们提出了一种数据共享策略来改进non-IID数据的FedAvg，通过全局共享一个包含每个类的样本的小型数据。这介绍了在准确率和中心化之间的权衡。实验表明，如果我们愿意集中和分发5％的共享数据，则可以在CIFAR-10上将准确性提高30％。

2 FedAvgonNon-IIDdata

在本节中，我们通过训练三个数据集上的代表性神经网络来演示FedAvg对non-IID数据的精度降低。

2.1 Experimental Setup

在这项工作中，我们使用卷积神经网络(CNNs)训练MNIST [6]， CIFAR-10[7]和Speech commands数据集[29]。MNIST和CIFAR-10是具有10个输出类的图像分类任务的数据集。语音命令数据集由35个单词组成，每个单词持续1秒。为了保持一致性，我们使用一个包含10个关键字的数据子集作为关键字发现(KWS)数据集。对于每个音频片段，我们提取30ms帧的10个MFCC特征，跨越20ms，生成50x10个特征，用于神经网络训练。对于MNIST和CIFAR-10，我们使用与[3]相同的CNN架构，而对于KWS，我们使用来自[1]的CNN架构。

训练集被均匀地划分为10个客户端。对于IID设置，每个客户端被随机分配十个类上的均匀分布。对于non-IID设置，数据按类排序并划分为两个极端情况: (a) 1-class non-IID，每个客户端只从一个类接收数据分区；(b) 2-class non-IID，将排序后的数据划分为20个分区，每个客户端从2类中随机分配2个分区。

我们对FedAvg算法使用与[3]相同的表示法：B，the batch size; E，the number of local epochs。以下参数用于FedAvg： MNIST, B = 10和100，E = 1和5,η= 0.01 ，衰减率decay rate = 0.995；对于CIFAR-10：B = 10和100，E = 1 和5,η= 0.1，衰减率decay rate = 0.992；对于KWS, B = 10和50,E = 1和5，η= 0.05和衰减率decay rate = 0.992。学习率针对每个数据集进行了优化，并在通信回合中呈指数衰减。对于SGD，学习速率和衰减速率是相同的，但是B要大10倍。这是因为来自FedAvg的全局模型在每次同步时在10个客户机上取平均值。使用IID数据的FedAvg应该与使用移动数据的SGD进行比较，batch size是后者的K倍，其中K是每次同步FedAvg时包含的客户端数量。

2.1 Experimental Results

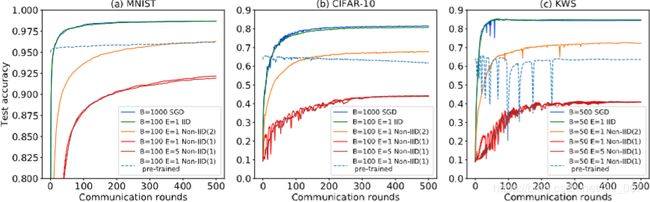
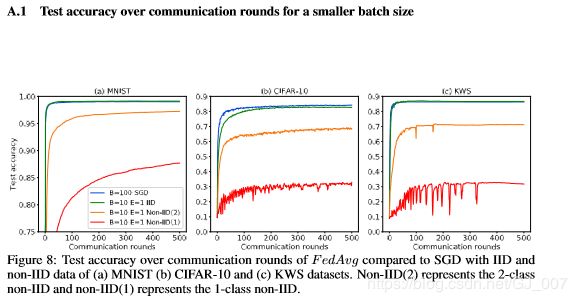
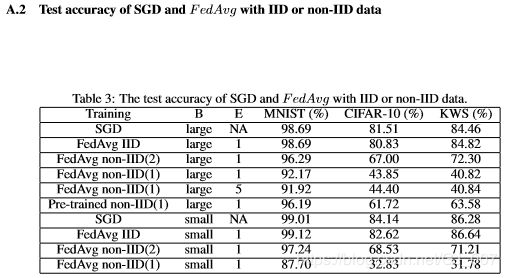
在IID实验中，批量为B的FedAvg的收敛曲线与三个数据集B×10的SGD的收敛曲线基本重合(图1)。对于CIFAR-10，仅观察到很小的差异，即B = 10的FedAvg收敛到82.62％，而B = 100的SGD收敛到84.14％（图A.1）。 因此，FedAvg对IID数据实现了SGD级别的测试准确性，这与[3]中的结果一致。

图1:与使用(a) MNIST (b) CIFAR-10和(c) KWS数据集的IID和non-IID数据的SGD相比，FedAvg通信轮的测试准确性。Non-IID(2)表示2类Non-IID, Non-IID(1)表示1类Non-IID。

在non-IID数据上，FedAvg的测试精度明显低于批量大小匹配的SGD(图1和A.1)。表1总结了non-IID数据的精度降低情况。最大精度降低发生在最极端的1类non-IID数据。而且，更大的本地epoch (E = 5)并不能减少损失。收敛曲线在E=1和E=5时大部分重合。此外，SGD预训练的CNN模型没有从non-IID数据的FedAvg训练中学习。对于CIFAR-10，当FedAvg对预先训练好的CNN进行non-IID数据训练时，准确性下降。因此，我们证明了FedAvg对non-IID数据的测试准确性下降。所有实验的检测精度如表A.2所示。请注意，本文中报告的SGD精度并不是最先进的[6,30,31,1]，但是我们训练的CNNs足以实现我们的目标，即评估non-IID数据上的联邦学习。

3 Weight Divergence due to Non-IID Data

在图1和A.1中，值得注意的是，2-class non-IID数据的缩减要小于1-classnon-IID数据。这表明FedAvg的准确性可能受到精确数据分布的影响，即，数据分布的偏态性。由于测试精度是由训练后的权值决定的，另一种比较FedAvg和SGD的方法是观察初始化权值相同的情况下，相对于SGD的权值的差异。称为weight divergence，其计算公式如下：

如图2所示，随着数据变得更加non-IID，从IID到2-class non-IID到1-class non-IID，所有层的weight divergence都在增加。因此，weight divergence和数据偏度之间的联系是可以预料的。第2节中出现的精度下降可以用weight divergence来理解，它量化了具有相同权值初始化的两个不同训练过程的weight divergence。在这一节中，我们正式分析了weight divergence的起源。在3.1节中，我们提供了一个说明文例和一个正式的命题来证明weight divergence的根本原因是由于每个 客户端的数据分布和人口分布之间的距离。具体地说，我们发现这样的距离可以用分布之间的搬土距离(EMD)来计算。然后，在第3.2节中，我们用证明EMD对FedAvg的 weight divergence和测试准确性的影响的实验来验证该命题。

3.1 Mathematical demonstration

我们正式定义了联邦学习的问题，并分析了weight divergence的根源。我们正式定义了联邦学习的问题，并分析了weight divergence的根源。 我们考虑在紧凑空间X和标签空间Y = |C|上定义的C类分类问题，其中|C| = {1，...，C}。数据点{x，y}遵循分布p在X×Y上分布。函数f：X→S映射到概率单纯形S，其中S = {z | 1，zi≥0，∀ i∈|C|}，其中fi表示第i类的概率。在假设类上参数化神经网络的权重。 我们用广泛使用的交叉熵损失定义损失：

为了简化分析，我们忽略了泛化误差，假设种损失是直接优化的。因此，学习问题就变成了

为了确定w，SGD迭代求解优化问题。设 为集中式设置中第t次更新后的权值。然后，集中式SGD进行如下更新：

在联邦学习中我们假设有K个客户端。令n(k)表示数据量，p(k)表示客户端k∈[k]上的数据分布。在每个客户端，本地SGD分别执行。在客户端k∈[k]上的迭代t时，本地SGD执行

然后，假设每T步都进行一次同步，令 表示第m次同步后计算的权值，则有

 

和 之间的差异可以通过图3中的插图来理解。当数据为IID时，对于每个客户端 和 之间的差异很小，并且在进行第m次同步后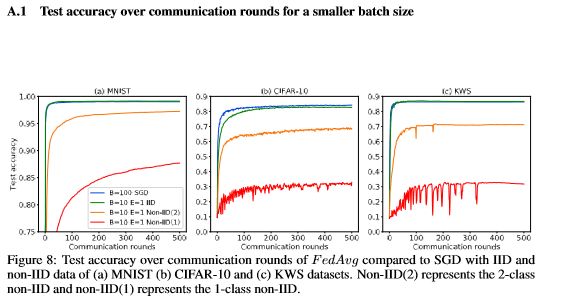， 仍然接近 当数据为non-IID时，对每个客户端k,由于数据间分布的距离， 和 之间的差异变得更大，并且累积的非常快，这使得 和 之间的差异越来越大。为了限制 和 之间的weight divergence，我们有以下提议。

Proposition 3.1.

给定K个客户端，每个客户端有n(k)个i.i.d样本，遵循客户端k∈[K]的分布p(k)。 如果对于每个类别i∈|C|， 是 ，并且每T步进行一次同步，那么对于第m个同步之后的weight divergence，我们有以下不等式，

命题3.1的详细证明见附录A.3。根据命题3.1，我们有如下评注。

Remark3.2. 第m次同步后的weight divergence主要来自两个部分，包括（m-1）次divergence后的weight divergence，即 。以及与实际分布相比，由客户端k上的数据分布的概率距离引起的weight divergence，即

Remark 3.3. 第（m -1）次同步之后的weight divergence被 放大。 由于a（k）≥1， 。因此，如果不同的客户端从联邦学习中的不同初始w开始，则 ，即使数据是IID，仍然会遇到较大的weight divergence，这会导致精度降低。

Remark 3.4. 当所有客户端都从与集中式设置相同的初始化开始时， 成为weight divergence的根本原因。 当距离测量定义为 时，该术语是客户端k上的数据分布与总体分布之间的EMD。 EMD的影响受学习速率η，同步之前的步数T和梯度 影响。

  基于命题3.1，我们验证了EMD是量化weight divergence的良好度量，因此可以在3.2节中使用non-IID数据量化FedAvg的测试准确性。

3.2 Experimental Validation

3.2.1 Experimental Setup

训练集被分类并划分为10个客户端，每个客户端M个示例。表2中列出的EMD选择了八个值。因为一个EMD可能存在各种分布，所以我们旨在生成五个分布来计算weight divergence和测试精度的平均值和变化。首先，为一个EMD生成一个10个类上的概率分布P。基于M和P，我们可以为一个客户机计算10个类上的实例数量。其次，通过将P的10个概率移动1个元素，生成一个新的分布P’。可以基于P’计算第二个客户端的示例数。对其他8个客户端重复此过程。因此，所有10个客户端在10个类中分布了M个示例，每个示例仅使用一次。最后，将上述两个步骤重复5次以为每个EMD生成5个分布.CNN由FedAvg进行了500多次通信回合，对上述过程中处理的数据进行训练。 有用于训练的关键参数：对于MNIST，B = 100，E = 1，η= 0.01，衰减率= 0.995； 对于CIFAR-10，B = 100，E = 1，η= 0.1，衰减率= 0.992; 对于KWS，B = 50，E = 1，η= 0.05，衰减率= 0.992。weight divergence是根据等式计算的。 （1）1次同步后（即1个通信回合）。

3.2.2 Weight Divergence vs. EMD

对于每个EMD，在5个分布上计算weight divergence的平均值和标准偏差。对于所有三个数据集，每层的weight divergence随EMD的增加而增加，如图4所示。每个数据集上所有SGD，IID和non-IID实验的初始权重均相同。因此，根据注释3.2，第1次同步之后的weight divergence不受第（m-1）个divergence的影响 ，因为当m = 1时为零。因此，图4中的结果支持命题3.1，即weight divergence的边界受EMD影响。在第一个卷积层和最后一个完全连接层中，这种影响更为显着。此外，CIFAR-10的最大weight divergence显著高于MNIST和KWS的最大差异，这受公式中的梯度项影响。（2）由于问题本身和不同的CNN架构。请注意，根据备注3.3，初始权重在客户端上也相同，以避免准确性损失，这与对具有不同初始化的模型求平均值时损失的显着增加是一致的[3，32]。

3.2.3 Test Accuracy vs. EMD

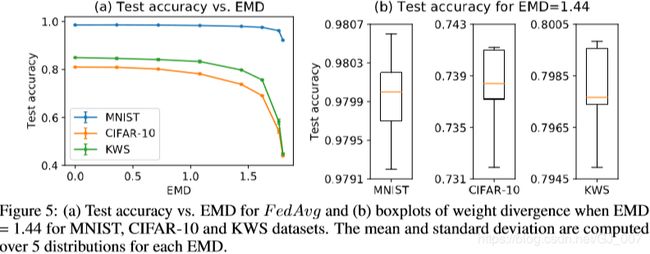
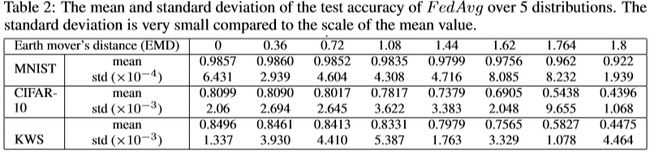
对于每个EMD，在相同的5个分布上计算出测试精度的平均值和标准偏差。结果总结在表2中，并相对于EMD绘制在图5中。对于所有三个数据集，测试精度随EMD降低。首先，降低的速率相对较小，随着数据变得更加non-IID而降低。因此，在将non-IID数据与IID平衡与提高FedAvg的准确性之间需要权衡。图中的误差线表示由于每个EMD的各种分布而导致的测试精度变化。为了更仔细地观察变化，方框图显示了EMD = 1.44时5次运行的测试准确性。此外，表2显示，MNIST的最大变化小于0.086％，CIFAR-10的最大变化小于2％，KWS的最大变化小于1％。因此，精度受EMD而非基础分布的影响。它表明，在给定数据分布的情况下，EMD可用于估计FedAvg的准确性。此外，MNIST的准确性最大降低为6.53％，CIFAR-10的准确性为37.03％，KWS的准确性为40.21％。这种差异可能受方程式中梯度的影响。 （2）视问题本身而定。

4 Proposed Solution

在本节中，我们提出了一个数据共享策略，通过创建一个在所有边缘设备之间全局共享的数据子集来改进non-IID数据的FedAvg。实验表明，在CIFAR-10数据集上，仅使用5%的全局共享数据，测试精度可提高约30%。

4.1 Motivation

如图5所示，相对于EMD而言，测试精度急剧下降超过某个阈值。因此，对于高度偏斜的non-IID数据，我们可以通过稍微降低EMD来显着提高测试精度。由于我们无法控制 客户端的数据，因此我们可以分配一小部分全局数据，其中包含从云到 客户端的各个类的统一分配。这符合典型的联邦学习设置的初始化阶段。另外，代替分配具有随机权重的模型，可以在全局共享数据上训练热身模型并将其分配给客户端。由于全局共享的数据可以减少客户端的EMD，因此有望提高测试准确性。

4.2 Data-sharing Strategy

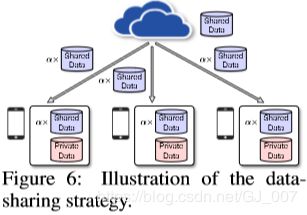
在这里，我们提出了一种在联邦学习环境中的数据共享策略，如图6所示。一个全局共享数据集G（由各个类的均匀分布组成）集中在云中。在FedAvg的初始化阶段，将在G上训练的预热模型和G的随机α部分分配给每个客户端。每个客户端的本地模型都接受了来自G的共享数据以及每个客户端的私有数据的训练。然后，云从客户端聚合本地模型，以使用FedAvg训练全局模型。有两个折衷：（a）测试精度的G大小之间的折衷，量化为 ，其中D代表来自 客户端的总数据（b）测试精度与α之间的权衡。为了解决这两个折衷，在CIFAR-10上进行了以下实验。

CIFAR-10训练集分为两部分，客户端部分D有40,000个示例，保留部分H有10,000个示例。D被划分为具有1类non-IID数据的10个客户端。H用于创建10个随机G’，β的范围从2.5％到25％。首先，将每个G全部与每个客户端的数据合并，并且FedAvg从头开始经过300多个通信回合，对10个CNN进行合并后数据的训练。在图7中针对β绘制了测试精度。其次，我们选择了两个特定的G’，即当β= 10％时为G10％，当β= 20％时为G20％。对于每个G，（a）在G上训练热身的CNN模型到约60％的测试准确度（b）仅将随机α部分与每个客户端的数据合并，然后在G上训练warm-up模型 合并的数据。测试精度相对于图7中的α进行了绘制。使用了与第3节相同的训练参数。

如图7（a）所示，随着β的增加，测试准确性提高了78.72％。即使将β= 10％降低，我们对于极端1类non-IID数据仍可以达到74.12％的准确性，相比之下，没有数据共享策略的准确性为44％。此外，事实证明，不必将整个G分发给客户端即可达到类似的准确性。相反，仅需要将G的随机部分分配给每个客户端。如图7（b）所示，预热模型的测试精度随α缓慢增加，对于G20％达到77.08％，对于G10％达到73.12％。特别是，在最初快速上升之后，当α从50％变为100％时，G20％和G10％的测试精度变化都小于1％。因此，我们可以通过适当选择α来进一步减少每个客户端实际接收的数据大小。例如，如果我们愿意在云中集中所有客户端数据的10％，并在联邦学习的初始化阶段将50％的全球共享数据随机分配给客户端以及一个热身模型，对于极端的1类non-IID数据，FedAvg的测试准确性可以提高30％，而每个客户端实际上仅接收到总数据的5％。

总之，数据共享策略为使用non-IID数据的联邦学习提供了一种解决方案。 可以根据问题和应用来调整全局共享数据集的大小和随机分布的分数（α）。初始化联邦学习后，该策略只需执行一次，因此通信成本不是主要问题。全局共享的数据是与客户数据不同的数据集，因此对隐私不敏感。

5 Conclusion

联邦学习将在分布式机器学习中扮演关键角色，在分布式机器学习中，数据隐私至关重要。不幸的是，如果每个边缘设备看到唯一的数据分布，模型训练的质量就会下降。在这项工作中，我们首先表明，对于高度偏斜的non-IID数据训练的神经网络，联邦学习的准确性显着降低了约55％。我们进一步表明，这种精度降低可以用weight divergence来解释，weight divergence可以通过每个设备上各个类别的分布与总体分布之间的EMD进行量化。作为解决方案，我们提出了一种策略，通过创建在所有边缘设备之间全局共享的一小部分数据来改善对non-IID数据的训练。实验表明，对于仅包含5％全局共享数据的CIFAR-10数据集，其准确性可以提高〜30％。要使联邦学习成为主流，仍然存在许多挑战，但是改进non-IID数据的模型训练对于在此领域取得进展至关重要。

A.3