最新论文笔记(+21)：Privacy-Preserving Byzantine-Robust Federated Learning via Blockchain Systems/ TIFS2022

Privacy-Preserving Byzantine-Robust Federated Learning via Blockchain Systems
可译为“利用区块链实现隐私保护的拜占庭鲁棒性联邦学习”

这篇是今年八月份被TIFS2022（CCF A）收录的文章，写的利用全同态加密和区块链技术解决联邦学习中隐私问题和可信问题（虽然区块链仅仅只是存储的作用，也稍微提了一下）。精读完这篇文章，整体感觉还不错，毕竟是CCF A类期刊。下面是自己读后感，根据自己的语言来做了一些笔记，也相当于回顾。其中，有理解不到位的地方望指正，建议读者还是看原文。

• 原文链接：Privacy-Preserving Byzantine-Robust Federated Learning via Blockchain Systems

一、文章背景

1.1 摘要和简要内容

摘要：由于中心化的联邦学习（Federated Learning，FL）框架和不可靠的用户，传统FL容易遭受恶意客户端和服务器的投毒攻击。本文设计了一个通过区块链系统实现隐私保护拜占庭鲁棒性联邦学习(PBFL）方案，来减轻中央服务器和恶意客户端的影响。利用余弦相似度来判断恶意客户端上传的恶意梯度。然后，采用全同态加密来提供安全的聚合。最后，使用区块链系统来促进透明的流程和法规的实施。形式化分析证明了本方案能达到收敛和提供隐私保护。

主要内容：

• 利用全同态加密（CKKS17）提供了一种隐私保护训练机制，减少了计算和通信开销，防止了攻击者窥探客户端的本地数据。
• 通过余弦相似度去除恶意梯度（感觉并没有去除，而是降低了“恶意梯度”的权重），提供了一个可信的全局模型，抵御了投毒攻击。
• 使用区块链来促进透明的流程，服务器链下计算（区块链实现去中心化的存储，不是去中心化训练，故还有服务器），将结果上传到区块链，实现了高效和可靠性。

1.2 联邦学习现存问题

（1）最常用的隐私保护联邦学习使用paillier同态加密算法来加密本地梯度，然而作者通过做实验比较了CKKS和paillier加密和解密向量所花的时间（CKKS: Homomorphic Encryption for Arithmetic of Approximate Numbers）。结果表明，CKKS算法效率更高，更适合处理大尺度向量和多参数网络模型。因此，本文使用CKKS加密局部梯度，以提高计算效率。

（2）隐私保护联邦学习（PPFL）仍受到投毒攻击。如经过训练的模型会对一个特定的类做出错误的预测，或全局模型对大量类做出错误预测。

（3）PPFL容易受到服务器恶意聚合和单点故障威胁。现有的FL方案在提高安全性和高效率的适合，无法抵抗客户端毒化攻击和避免服务器恶意行为，且在实践中扩展性不强。

1.3 CKKS全同态加密

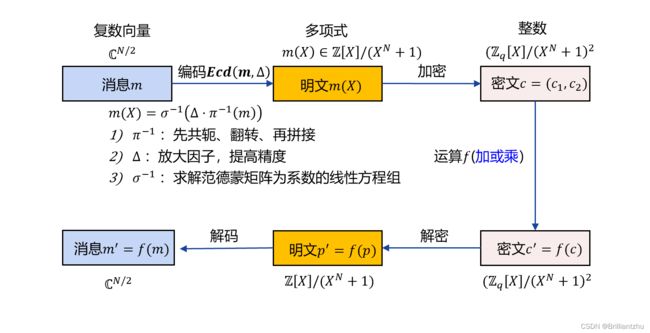
本文主要用到的是全同态加密（CKKS）技术，自己也在看这篇文章前，花了三四天读CKKS论文，结合他人对CKKS的介绍才懂了这个全同态加密方法。可以参考全同态CKKS方案解析.

注意以下几个点：

• 全同态加密满足加同态性质，即两个明文分别加密后相加等于明文先相加再加密的结果（$E(m_1)+E(m_2)=E(m_1+m_2)$)。
• 全同态加密满足乘同态性质，即两个明文分别加密后相乘等于明文先相乘再加密的结果（$E(m_1)\cdot E(m_2)=E(m_1\cdot m_2)$)。

具体流程如下：

二、主要内容

将原联邦学习中的服务器扩展为两个“诚实且好奇”的服务器，分别为Verifier和Solver，它们不共谋。

由Solver服务器设置一个小而干净的根数据集$D_0$，并基于它维护一个模型$w_0$，根据算出来的梯度$g_i^0$和Clients上传的梯度$g_i^j$的余弦相似度，以此来去除恶意的梯度。

本篇文章只有一个框架图，具体发送什么并不是很清晰，为了便于自身理解，画了一个流程图如下：

首先初始化，密钥生成中心为Verifier和Client生成公私钥对，分别为$(p{k}_v,s{k}_v)$，$(p{k}_x,s{k}_x)$。

（1）本地计算

• 1）局部训练：$g_i^j=\nabla L(w_i^j,D_j)$。假设第$i$次迭代，每个客户端$C_j$用本地数据集$D_j$和局部模型$w_i^j$对损失函数求导，算出局部梯度$g_i^j$。
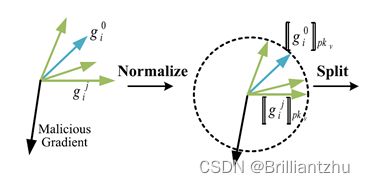
• 2）归一化：$g_i^j=\frac{g_i^j}{||g_i^j||}$。由于聚合规则基于余弦相似度策略，需要对局部梯度进行归一化处理，将余弦相似度转化为向量的内积。另外，将向量归一化减轻了恶意梯度的影响。

• 3）全同态加密：$[[g_i^j]{]}_{p{k}_v}$。客户端使用Verifier的公钥$p{k}_v$加密本地归一化后的梯度$g_i^j$，将其上传给Solver。
• 4）模型更新：$w_i\leftarrow w_{i-1}-\alpha g_i^j$。客户端$C_j$从区块链下载最新的全局模型，并用自己的私钥$s{k}_x$解密得到明文(感觉这里存在一点点问题，在最后我会说明），再进行模型更新。

（2）归一化判断

很自然，当客户端上传归一化的梯度后，需要Solver判断收到的梯度是否真的进行了归一化处理，防止恶意客户端行为。所以，当Solver收到$[[g_i^j]{]}_{p{k}_v}$后，计算其内积，再发送给Verifier，即$[[r_1]{]}_{p{k}_v}=[[g_i^j]{]}_{p{k}_v}\odot [[g_i^j]{]}_{p{k}_v}$。这里就要用到乘同态性质，两个向量分别加密后相乘等于两个向量先相乘再加密的结果。具体步骤如下：

• 假设$[[g_i^j]{]}_{p{k}_v}=[[(p_1,p_2,\cdots ,p_{n^{\ast }})]{]}_{p{k}_v}$。
• 这两个向量相乘为$[[g_i^j\cdot g_i^j]{]}_{p{k}_v}=[[(p_1^2,p_2^2,\cdots ,p_{n^{\ast }}^2)]{]}_{p{k}_v}$。
• 利用CKKS旋转操作，旋转一次为$[[(p_2^2,p_3^2,\cdots ,p_{n^{\ast }}^2,p_1^2)]{]}_{p{k}_v}$，重复旋转$(n^{\ast }-1)$次后再相加，并得到$[[(r_1,r_2,\cdots ,r_{n^{\ast }})]{]}_{p{k}_v}$。
• 计算$[[(r_1,r_2,\cdots ,r_{n^{\ast }})]{]}_{p{k}_v}$和$[1,0,\cdots ,0,0]$的乘积，得到$[[r_1]{]}_{p{k}_v}$。

然后将所有的$[[r_1]{]}_{p{k}_v}$发送给Verifier进行验证，Verifier将得到诚实客户端的列表$C$存储到区块链上，并发给Solver。不难看出，如果梯度真实地归一化处理后，两个向量的内积和应该为1，即$r_1=1$，只需判断$[[r_1]{]}_{p{k}_v}=[[1]{]}_{p{k}_v}？$即可。

这里仅仅是判断梯度是否归一化处理，恶意客户端也可以诚实的归一化处理吧，只是他的梯度方向偏离较大。

（3）模型聚合

• 1）训练可信数据集$D_0$，并获得梯度$[[g_i^0]{]}_{p{k}_v}$。当Solver收到诚实客户端列表$C$后，需要进行聚合操作了。但还存在一个问题，要给所有客户端上传的梯度分配一个权重，让与梯度$g_i^0$方向更相似的局部梯度拥有更高的权重，反之越偏离梯度$g_i^0$方向的局部梯度赋予更小的权重。通过余弦相似度计算：
  $$\begin{gathered} [[c{s}_i^j]{]}_{p{k}_v}=[[g_i^0]{]}_{p{k}_v}\odot [[g_i^j]{]}_{p{k}_v} \\ s.t.||g_i^0||=||g_i^j||=1 \end{gathered}$$
  
  其中$c{s}_i^j$可以描述为两个向量的相似度。同样，由于归一化后，两个向量之间的余弦相似度可以转换为内积。现在要做的就是将与$g_i^0$方向的局部梯度去除。这里定义了一个ReLU函数
  $$S_i^j=ReLU(c{s}_i^j)=\{\begin{array}{ll}c{s}_i^j,& \text{if csij>0}\\ 0,& \text{if csij≤0}\end{array}$$
  其中，$S_i^j$看作是梯度的权重。通过上式可知，ReLU函数就是比较自变量和0之间的大小关系，而上面只知道加密后的$[[c{s}_i^j]{]}_{p{k}_v}$，因此需要一种在密文状态下的比较方法，来比较$[[c{s}_i^j]{]}_{p{k}_v}$和$[[0]{]}_{p{k}_v}$的大小关系。

本文采用了亚密上CKKL19全同态加密中密文比较方法。但是这篇文章只给出了在[0,1]范围内同态密码比较的一种数值方法。但是余弦相似度落在[-1,1]范围内，因此无法直接拿来用，需要做一个转换使其满足要求：

• 先给$[[c{s}_i^j]{]}_{p{k}_v}$加$[[1]]$，使结果的明文落在[0,2]上。
• 再将结果乘以1/2，使得范围满足要求。(注意0对应于1/2）

因此，转换ReLU函数变成了ReLU’函数：
$$[[S_i^j]]=ReLU([[c{s}_i^j]])=\{\begin{array}{ll}\frac{1}{2}([[c{s}_i^j]]+[[1]]),& \text{if 21([[csij]]+[[1]])>[[1/2]]}\\ [[1/2]],& \text{if 21([[csij]]+[[1]])≤[[1/2]]}\end{array}$$
然后再利用Algorithm 4同态比较方法，得到权重的密文$[[S_i^j]]$。

• 2）Solver获得所有Client的分数$[[S_i^j]]$。但这个分数的密文还只是变换后的分数，则原始分数应该为$[[S_i^j]{]}_{p{k}_v}^{\prime }=2\cdot [[S_i^j]{]}_{p{k}_v}-[[1]{]}_{p{k}_v}$

  • 计算$[[sum]{]}_{p{k}_v}={\sum }_{f=1}^{|C|}[[S_i^f]{]}_{p{k}_v}^{\prime }$，并将其存储到区块链上。
  • 随机选取$n^{\ast }$维向量$V$和$V^{n^{\ast }}$，并计算得到$V\cdot [[S_i^f]{]}_{p{k}_v}^{\prime }$和$V^{n^{\ast }}\cdot [[g_i^j]{]}_{p{k}_v}$，并将其存储到区块链上。

• 3）Verifier执行以下加解密操作。

  • 利用$s{k}_v$解密它们，并获得$sum$， $V\cdot S_i^{j^{\prime }}$和$V^{n^{\ast }}\cdot g_i^j$。
  • 再利用$p{k}_x$加密它们，计算得到$[[V\cdot S_i^{j^{\prime }}]{]}_{p{k}_x}$和$[[V^{n^{\ast }}\cdot g_i^j]{]}_{p{k}_x}$，并连同$sum$一起发送上链。

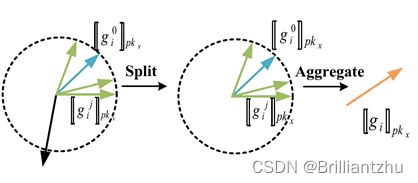
• 4）Solver执行以下聚合操作。

  • 利用$1/V$乘以$[[V\cdot S_i^{j^{\prime }}]{]}_{p{k}_x}$，获得$[[S_i^{j^{\prime }}]{]}_{p{k}_x}$。
  • 利用$1/V^{n^{\ast }}$乘以$[[V^{n^{\ast }}\cdot g_i^j]{]}_{p{k}_x}$，获得$[[g_i^j]{]}_{p{k}_x}$。
  • 根据它们的分数来聚合梯度：
    $$\begin{gathered} [[g_i^j]{]}_{p{k}_x}=\frac{1}{sum}\sum _{j=1}^{|C|}[[S_i^{j^{\prime }}]{]}_{p{k}_x}\cdot [[g_i^j]{]}_{p{k}_x} \\ =\frac{1}{sum}\sum _{j=1}^{|C|}ReLU([[g_i^0]{]}_{p{k}_x}\odot [[g_i^j]{]}_{p{k}_x})\cdot [[g_i^j]{]}_{p{k}_x} \end{gathered}$$

由此看出，在本方案中Verifier和Solver不能得到除求和以外的任何信息，即使获得了求和结果也无法从中得到有价值的信息。除非两个合谋，但前提已经假设不能合谋。此外，Solver和Verifier都需要向智能合约缴纳保证金，并将在任务结束时以客户端的保证金作为奖励。

区块链的作用：存储中间参数信息，保证这些信息是可信，无法篡改的。

三、性能评估

数据集：采用MNIST和FashionMNIST，分别选取200个数据作为数据集$D_0$。
实验平台：Ethereum区块链设置，使用Truffle部署在私有区块链上，Tenseal库实现CKKS算法。

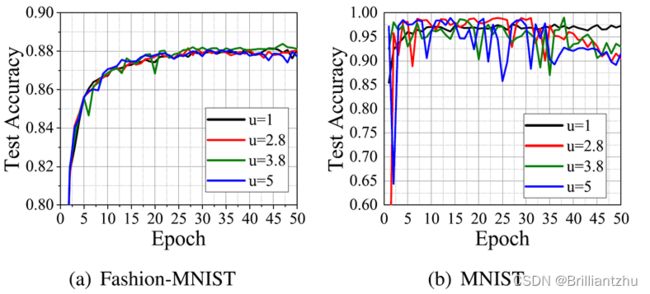
• 1）鲁棒性评估

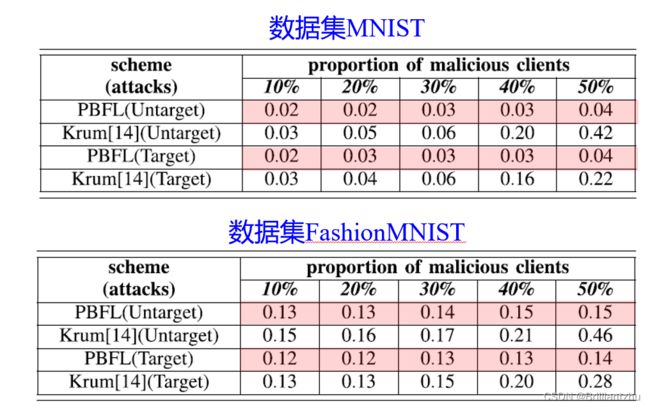
结论：在目标攻击和非目标攻击和不同比例恶意客户端的情况下，对不同类型的投毒攻击仍能达到鲁棒性和准确性的目标。

• 2）准确性评估

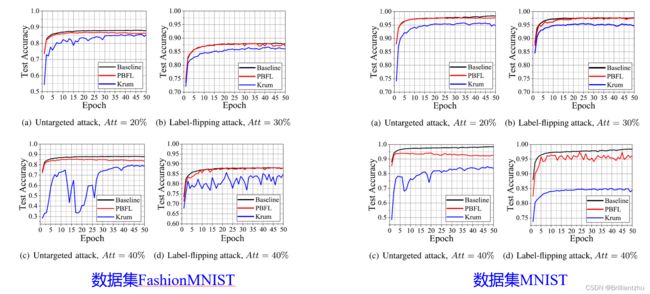
结论：在目标攻击和非目标攻击和不同比例恶意客户端的情况下，几乎能够达到与Baseline一样的准确性，比Krum算法好很多。

• 3）区块链上的开销
  
  结论：本方案实现了较低的gas消耗，因为把计算负担留给了线下服务器，只把结果上传到区块链，这大大降低了gas的消耗。

• 4）非平衡数据下的性能

• 

考虑现实原因，根数据集可能是不均匀分布的。假设根数据集共有10个类的标签，且下一个类总比前一类多$n^{\prime }$个，则数据非平衡程度为$u=(a+9\ast n^{\prime })/a$。

结论：数据集$D_0$中的分布差异不会对结果产生太大影响，结果显示可以忽略数据分布差异对结果的影响。

四、总结与思考

个人觉得这篇文章比较新颖的点有三处：

• 1）要求服务器收集一个小而干净的根数据集，来抵御投毒攻击，以维护模型。
• 2）将传统单服务器分为了两个不共谋的诚实且好奇的服务器，避免了服务器端恶意行为。
• 3）提出了一种全同态加密（CKKS）的隐私保护机制，以减少了计算和通信开销。

疑问：

• 1）在Algorithm1的本地计算中，每个客户端从区块链中下载$[[w_{i-1}]{]}_{p{k}_x}$，再用各自的$s{k}_x$解密，也就是说上一轮要用每个客户端的公钥去加密同一个模型$w_{i-1}$，然后客户端才能用自身的私钥解密，这不会产生非常大的开销嘛，是否有必要？（可能所有客户端公用一个公私钥对）
• 2）最后虽然作者模拟了根数据集的非平衡分布，但是客户端的训练数据集还是均匀分布的，而联邦学习中的数据应该是非独立同分布，要是再增加这个实验就好啦。
• 3）这个小而干净的根数据集是如何选取？这在FL中本身就是一个难题。