【机器学习】支持向量机(二)——序列最小最优化(SMO)算法
一、问题引入
上篇博文我们已经把支持向量机的学习问题化为求解凸二次规划问题,并求出了它的最优解。但是当训练样本容量很大时,使用二次规划的算法往往变得非常低效,以致无法使用。因此,我们需要实现一个高效的支持向量机学习算法。John Platt提出的序列最小最优化(SMO)算法便是这些高效算法中的一种。SMO算法是一种启发式算法,它将原优化问题分解为多个小优化问题来求解,并且对这些小优化问题进行顺序求解得到的结果作为作为整体的结果,有些动态规划的思想。
二、问题分析
以下只把算法列出,不予证明。证明过程可查看John Platte的相关论文或《统计学习方法》。
SMO算法要求解的问题是:

其子问题可以写成:

为了叙述方便,记:

子问题未经约束的解是:

其中:

经约束后的解是:
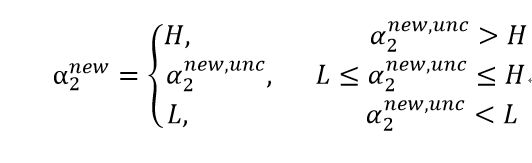
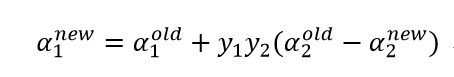
其中:

变量的选择步骤如下:
(1)启发式策略1:第一个变量的选择为外层循环,先选取违反KKT条件最严重的样本点,KKT条件即:
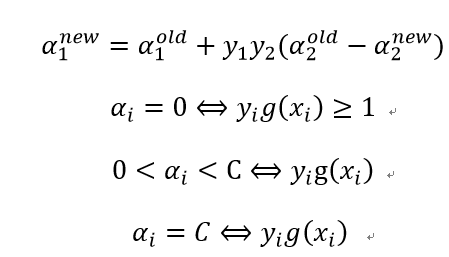
再用“启发式策略2”选择另外一个变量并进行这两个变量的优化(之所以选择非边界样本是为了提高找到违反KKT条件的点的机会),最后,如果上述非边界样本中没有违反KKT条件的样本,则再从整个样本中去找,直到所有样本中没有需要改变的变量或者满足其它停止条件为止。
(2)启发式策略2:第二个变量的选择为内层循环,为了加快α2的迭代速度,应使其对应的|E1-E2|最大。
(3)计算阈值b:

三、代码实现(Python)
1.简化版
此算法实现时的内层循环采用随机选择的方式,未使用启发式规则。
(1)主算法实现
# 随机选择一个不等于i的j
def selectJrand(i,m):
j = i
while (j == i):
j = int(random.uniform(0,m))
return j
# 上下界约束
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
# 主算法
# 输入参数:训练数据集、类别标签(y)、惩罚参数C、容错率、最大迭代次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
b = 0; m,n = shape(dataMatrix)
alphas = mat(zeros((m,1)))
iter = 0 # 迭代次数
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
gXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b # 计算g(xi)
Ei = gXi - float(labelMat[i])
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):# 检查是否满足KKT条件
j = selectJrand(i,m) # 随机选择第二个变量
gXj = float(multiply(alphas,labelMat).T * (dataMatrix*dataMatrix[j,:].T)) + b
Ej = gXj - float(labelMat[j])
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
if (labelMat[i] != labelMat[j]): # 计算约束上下界
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
print('L==H'); continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0:
print('eta>=0'); continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta # 计算α2,并满足约束条件
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): # 内层循环结束条件
print('j not moving enough'); continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j]) # 计算第一个变量
# 计算阈值b
b1 = b - Ei - labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej - labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
print ('iter: %d i:%d, pairs changed %d' % (iter,i,alphaPairsChanged))
if alphaPairsChanged == 0:
iter += 1
else:
iter = 0
print('iteration number: %d' % iter)
return b,alphas
# 计算法向量w
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr); labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w(2)导入数据并绘图:
dataMat, labelArr = loadDataSet('testSet.txt')
dataArr = array(dataMat)
xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
markers =[]
colors =[]
m = shape(dataArr)[0]
for i in range(m):
if (int(labelArr[i])) == -1:
xcord0.append(dataArr[i,0]); ycord0.append(dataArr[i,1])
else:
xcord1.append(dataArr[i,0]); ycord1.append(dataArr[i,1])
b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40) # 计算相关参数
alphas = alphas.A
w = calcWs(alphas, dataArr, labelArr) # 计算法向量
sptVec = []
for i in range(m): # 找出支持向量
if alphas[i] > 0.0:
sptVec.append(tuple(dataArr[i]))
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(xcord0, ycord0, marker = 's', s = 50, c = 'blue')
ax.scatter(xcord1, ycord1, marker = 'o', s = 50, c = 'green')
plt.title('Support Vectors. C = %0.2f' % C)
for i in range(len(sptVec)):
circle = Circle(sptVec[i], 0.5, facecolor = 'none', edgecolor = (0,0.8,0.8), linewidth = 3, alpha = 0.8)
ax.add_patch(circle)
x = arange(-2.0, 12.0, 0.1)
y = (-float(w[0])*x - float(b)) / float(w[1])
ax.plot(x, y, c = 'red', linewidth = 2)
ax.axis([-2,12,-8,6])
plt.show()dataMat, labelArr = loadDataSet('testSet.txt')
dataArr = array(dataMat)
xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
markers =[]
colors =[]
m = shape(dataArr)[0]
for i in range(m):
if (int(labelArr[i])) == -1:
xcord0.append(dataArr[i,0]); ycord0.append(dataArr[i,1])
else:
xcord1.append(dataArr[i,0]); ycord1.append(dataArr[i,1])
C = 0.01
b, alphas = smoSimple(dataArr, labelArr, C, 0.001, 100) # 计算相关参数
alphas = alphas.A
w = calcWs(alphas, dataArr, labelArr) # 计算法向量
sptVec = []
for i in range(m): # 找出支持向量
if alphas[i] > 0.0:
sptVec.append(tuple(dataArr[i]))
print(end-start)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(xcord0, ycord0, marker = 's', s = 50, c = 'blue')
ax.scatter(xcord1, ycord1, marker = 'o', s = 50, c = 'green')
plt.title('Support Vectors. C = %0.2f' % C)
for i in range(len(sptVec)):
circle = Circle(sptVec[i], 0.5, facecolor = 'none', edgecolor = (0,0.8,0.8), linewidth = 3, alpha = 0.8)
ax.add_patch(circle)
x = arange(-2.0, 12.0, 0.1)
y = (-float(w[0])*x - float(b)) / float(w[1])
ax.plot(x, y, c = 'red', linewidth = 2)
ax.axis([-2,12,-8,6])
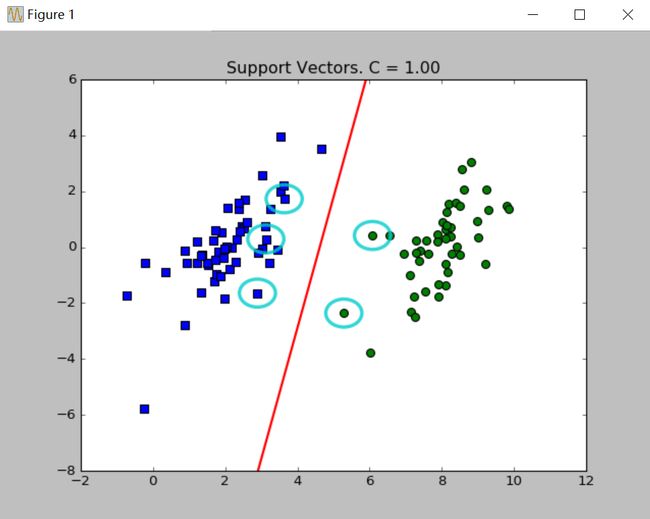
plt.show()分别取C=0.01、C=1绘制效果如下:
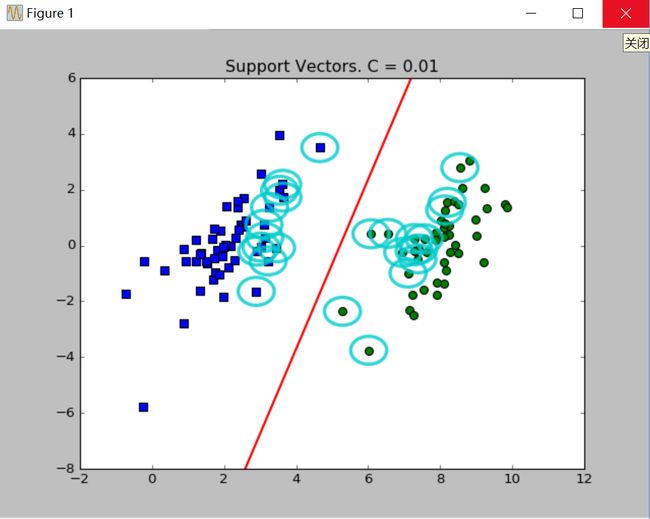

图中绘出了决策边界和圈起的支持向量。关于参数C在上篇博文已经说过,C值取得越大,对误差的惩罚越大,相应的支持向量越多。
2.使用启发式规则完整版
上述算法运行效率是很低的,因为我们选择第二个时是随机选择的,没有确保|E1-E2|最大,此时α2的步长不是最大的,迭代速度会很慢。因此我们的优化策略是,把所有的E值存在一个列表中,选择最大的E值对应的α值来更新α2。
(1)封装参数,并且多次重复的代码必须提取出来:
class optStruct:
def __init__(self, dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m, 1)))
self.b = 0
self.eCache = mat(zeros((self.m, 2)))
% E值多次计算,提取出来
def calcEk(oS, k):
fXk = float(multiply(oS.alphas, oS.labelMat).T*(oS.X*oS.X[k, :].T)) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek(2)启发式策略:
# 启发式策略选择第二个变量
def selectJ(i, oS, Ei):
maxK = -1;maxDeltaE = 0;Ej = 0
oS.eCache[i] = [1, Ei]
validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList:
if k==i:
continue
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE): # 保证返回的是E值最大时对应的α2
maxK = k;maxDeltaE = deltaE;Ej = Ek
return maxK, Ej
else:
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
# 存入缓存列表中
def updateEk(oS, k):
Ek = calcEk(oS, k)
oS.eCache[k] = [1, Ek](3)优化后的算法:
# 内层循环
def innerLoop(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei)
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print('L==H'); return 0
eta = 2.0 * oS.X[i,:] * oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
if eta >= 0:
print(eta>=0); return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print('j not moving enough'); return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
updateEk(oS, i)
b1 = oS.b - Ei - oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
b2 = oS.b - Ej - oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2)/2.0
return 1
else:
return 0
# 外层循环
def smoCompleted(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)): #full Platt SMO
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C , toler)
iter = 0
entireSet = True; alphaPairsChanged = 0
# 当迭代次数超过指定的最大值或者遍历整个数据集都未对任何乘子进行修改时退出循环
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: # 遍历所有的值
for i in range(oS.m):
alphaPairsChanged += innerLoop(i,oS)
print('fullSet, iter: %d i:%d, pairs changed %d' % (iter,i,alphaPairsChanged))
iter += 1
else: # 遍历非边界值
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerLoop(i,oS)
print('non-bound, iter: %d i:%d, pairs changed %d' % (iter,i,alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False # 设定跳出循环条件
elif (alphaPairsChanged == 0):
entireSet = True
print('iteration number: %d' % iter)
return oS.b,oS.alphas (4)导入数据并绘图:
绘图程序并没有多少改变,只是改变调用优化后的函数即可。分别选取C=0.01、C=1绘图如下:

四、总结
经我本机测试,在同样参数的情况下,未经优化的算法迭代100次需要耗时3.658s,而优化后的算法迭代100次平均需要耗时0.171s,差距是非常巨大的。而且机器学习算法经常用来处理大数据,未经优化的算法仅仅100条数据就耗时3秒多,如果是亿万条数据,那不是得跑个好几天?可见优化算法的重要性,尤其是在这个效率就是金钱的时代!有时一个人的伟大之处不一定是创造了什么,而是在前人的基础上不断加以修正、完善、提高。假如有朝一日我也能把这个算法的运行时间再减少0.001秒,想必我已经在这个领域上独领风骚了吧,哈哈!开个玩笑,更刻苦的学习之路还在后头,支持向量机我也只是了解了皮毛,还需要不断深入学习。之后我希望能抽个时间使用这个算法做一个小项目,加油!