Logistec Regression(逻辑回归)的相关讨论
文章目录
- 一、逻辑回归
- 二、最大似然估计和最大后验估计
- 三、最小二乘法和最大似然估计
- 四、混淆矩阵
一、逻辑回归
1. 定义
对数几率回归(也称“逻辑回归”)(英语:Logistic regression 或logit regression),即对数几率模型(英语:Logit model,也译作“逻辑模型”、“评定模型”、“分类评定模型”)是离散选择法模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。
单单从名称上看,很容易将“逻辑回归”当作的侧重点放在“回归”连个字眼上。但是在机器学习中,Logistic regression的主要解决的却是分类问题;首先从处理的数据类型上来看,LR处理的数据多是离散化标签数据,对数据进行分类。最简单就是二分类问题中的正例和负例,如检查一个人是否患有肿瘤。
在此借用Andrew NG的讲义,有如下图所示,X为数据点——肿瘤的大小,Y为观测值——是否是恶性肿瘤。通过构建线性回归模型,如 h θ ( x ) h_\theta(x) hθ(x)所示,构建线性回归模型后,即可以根据肿瘤大小,预测是否为恶性肿瘤 h θ ( x ) ≥ 0.5 h_\theta(x)\ge0.5 hθ(x)≥0.5为恶性, h θ ( x ) < 0.5 h_\theta(x)<0.5 hθ(x)<0.5为良性。
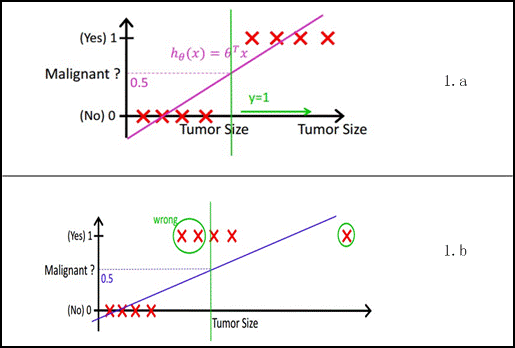
由于线性回归在整个实数域内敏感度一致,而分类范围需要在[0, 1]。逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型。 逻辑回归其实仅为在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,逻辑回归成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。
假设: h θ ( x ) = g ( θ T x ) = 1 1 + e − e T x h_\theta(x) = g(\theta^Tx) = \frac{1}{1 + e^{-e^Tx}} hθ(x)=g(θTx)=1+e−eTx1, g ( z ) = 1 1 + e z g(z) = \frac{1}{1+e^z} g(z)=1+ez1
因为y的取值为y = {0, 1},所以:
P ( y = 1 ∣ y , θ ) = h θ ( x ) P(y = 1|y, \theta) = h_\theta(x) P(y=1∣y,θ)=hθ(x)
P ( y = 0 ∣ y , θ ) = 1 − h θ ( x ) P(y = 0|y, \theta) = 1 - h_\theta(x) P(y=0∣y,θ)=1−hθ(x)
P ( x ∣ y , θ ) = h θ ( x ) y ( 1 − h θ ( x ) ) 1 − y P(x|y, \theta) = h_\theta(x)^y(1 - h_\theta(x))^{1-y} P(x∣y,θ)=hθ(x)y(1−hθ(x))1−y
对于训练数据集,特征数据 x = ( x 1 , x 2 , … , x m ) x=(x_1, x_2, … , x_m) x=(x1,x2,…,xm)和对应的分类数据 y = ( y 1 , y 2 , … , y m ) y=(y_1, y_2, … , y_m) y=(y1,y2,…,ym)。构建逻辑回归模型 h ( θ ) h(\theta) h(θ),最典型的构建方法便是应用极大似然估计。那么,极大似然函数为: L ( θ ) = ∏ i = 1 m P ( y ∣ x , θ ) = ∏ i = 1 m h θ ( x , θ ) y ( 1 − h θ ( x , θ ) ) 1 − y L(\theta) = \prod_{i=1}^m P(y|x, \theta) = \prod_{i=1}^m h_\theta(x, \theta)^y(1 - h_\theta(x, \theta))^{1-y} L(θ)=i=1∏mP(y∣x,θ)=i=1∏mhθ(x,θ)y(1−hθ(x,θ))1−y两边同时取对数( log \log log)
log ( L ( θ ) ) = ∑ i = 1 m [ y log ( h θ ( x ) ) + ( 1 − y ) log ( 1 − h θ ( x ) ) ] \log(L(\theta)) = \sum_{i=1}^m [y\log(h_\theta(x)) + (1-y)\log(1-h_\theta(x))] log(L(θ))=i=1∑m[ylog(hθ(x))+(1−y)log(1−hθ(x))] c o s t ( h θ ( x ) , y ) = − log ( L θ ) = − ∑ i = 1 m [ y log ( h θ ( x ) − ( 1 − y ) log ( 1 − h θ ( x ) ) ) ] cost(h_\theta(x), y) = -\log (L_\theta) = -\sum_{i=1}^m[y\log (h_\theta(x) - (1-y)\log(1-h_\theta(x)))] cost(hθ(x),y)=−log(Lθ)=−i=1∑m[ylog(hθ(x)−(1−y)log(1−hθ(x)))] J ( θ ) = − 1 m ∑ i = 1 m [ y i log ( h θ ( x i ) ) + ( 1 − y ) log ( 1 − h θ ( x i ) ) ] J(\theta) = -\frac{1}{m}\sum_{i=1}^m[y_i\log(h_\theta(x_i)) + (1-y)\log(1-h_\theta(x_i))] J(θ)=−m1i=1∑m[yilog(hθ(xi))+(1−y)log(1−hθ(xi))]
代入 h θ ( x ) = g ( θ T x ) = 1 1 + e − e T x h_\theta(x) = g(\theta^Tx) = \frac{1}{1 + e^{-e^Tx}} hθ(x)=g(θTx)=1+e−eTx1得:
J ( θ ) = − y log ( 1 + e − θ T x i ) − ( 1 − y i ) log ( 1 + e θ T x i ) J(\theta) = -y \log(1 + e^{-\theta^Tx_i}) - (1-y_i)\log(1+ e^{\theta^Tx_i}) J(θ)=−ylog(1+e−θTxi)−(1−yi)log(1+eθTxi)采用梯度下降法计算得出: ∂ J ( θ ) ∂ θ i = 1 m ∑ i = 1 m [ h θ ( x i ) − y i ] x i j \frac{\partial J(\theta)}{\partial\theta_i} = \frac{1}{m}\sum_{i=1}^m[h_\theta(x_i) - y_i] x_{ij} ∂θi∂J(θ)=m1i=1∑m[hθ(xi)−yi]xij
演算手稿:
二、最大似然估计和最大后验估计
最大似然估计定义:
给定一个概率分布D,已知其概率密度函数(连续分布)或概率质量函数(离散分布)为 f D f_D fD,以及一个分布参数 θ \theta θ,我们可以从这个分布中抽出一个具有n个值的采样 X 1 , X 2 , ⋯ , X n X_1,X_{2},\cdots ,X_n X1,X2,⋯,Xn,利用 f D f_D fD计算出其似然函数: L ( θ ∣ x 1 , ⋯ , x n ) = f θ ( x 1 , ⋯ , x n ) L(\theta | x_1, \cdots,x_n) = f_\theta(x_1,\cdots,x_n) L(θ∣x1,⋯,xn)=fθ(x1,⋯,xn)若D是离散分布 f θ f_\theta fθ,即是在参数为 θ \theta θ时观测到这一采样的概率。若其是连续分布, f θ f_\theta fθ则为 X 1 , X 2 , ⋯ , X n X_1,X_{2},\cdots ,X_n X1,X2,⋯,Xn联合分布的概率密度函数在观测值处的取值。一旦我们获得 X 1 , X 2 , ⋯ , X n X_1,X_{2},\cdots ,X_n X1,X2,⋯,Xn,我们就能求得一个关于 θ \theta θ的估计。最大似然估计会寻找关于 θ \theta θ的最可能的值(即,在所有可能的 θ \theta θ取值中,寻找一个值使这个采样的“可能性”最大化)。从数学上来说,我们可以在 θ \theta θ的所有可能取值中寻找一个值使得似然函数取到最大值。这个使可能性最大的 θ ^ \hat{\theta} θ^值即称为 θ \theta θ的最大似然估计。由定义可知,最大似然估计是样本的函数。
定义:
在贝叶斯统计学中,“最大后验概率估计”是后验概率分布的众数。利用最大后验概率估计可以获得对实验数据中无法直接观察到的量的点估计。它与最大似然估计中的经典方法有密切关系,但是它使用了一个增广的优化目标,进一步考虑了被估计量的先验概率分布。所以最大后验概率估计可以看作是规则化的最大似然估计。
假设我们需要根据观察数据 x x x计没有观察到的总体参数 θ \theta θ,让 f f f作为 x x x 的采样分布,这样 f ( x ∣ θ ) f(x|\theta) f(x∣θ) 就是总体参数为 θ \theta θ时 x x x的概率。函数 θ → f ( x ∣ θ ) \theta\to f(x|\theta) θ→f(x∣θ)即为似然函数。其估计: θ ^ M L = arg max θ f ( x ∣ θ ) \hat{\theta}_{ML} = \arg \max\limits_{\theta}f(x|\theta) θ^ML=argθmaxf(x∣θ)就是 θ \theta θ的最大似然估计。
假设 θ \theta θ存在一个先验分布 g g g,这就允许我们将 θ \theta θ 作为 贝叶斯统计中的随机变量,这样 θ \theta θ的后验分布就是: θ → f ( x ∣ θ ) g ( θ ) f θ f ( x ∣ θ ′ ) g ( θ ′ ) d θ ′ \theta \to \frac{f(x|\theta)g(\theta)}{f_\theta f(x|\theta ^ {'})g(\theta^{'})d\theta^{'}} θ→fθf(x∣θ′)g(θ′)dθ′f(x∣θ)g(θ)其中 θ \theta θ为 g g g的gomain,这是贝叶斯定理的直接应用。
最后验估计方法于是估计 θ \theta θ为这个随机变量的后验分布的众数: θ ^ M A P = arg max θ f ( x ∣ θ ) g ( θ ) f θ f ( x ∣ θ ′ ) g ( θ ′ ) d θ ′ = = arg max θ f ( x ∣ θ ) g ( θ ) \hat{\theta}_{MAP} = \arg \max\limits_{\theta}\frac{f(x|\theta)g(\theta)}{f_\theta f(x|\theta ^ {'})g(\theta^{'})d\theta^{'}} = = \arg \max\limits_{\theta}f(x|\theta)g(\theta) θ^MAP=argθmaxfθf(x∣θ′)g(θ′)dθ′f(x∣θ)g(θ)==argθmaxf(x∣θ)g(θ)后验分布的分母与 θ \theta θ无关,所以在优化过程中不起作用。注意当先验 g g g是常数函数时最大后验估计与最大似然估计重合。
最大后验估计可以用以下几种方法计算:
- 解析方法,当后验分布的模能够用 解析解 方式表示的时候用这种方法。当使用共轭先验 的时候就是这种情况。
- 通过如共扼积分法或者牛顿法这样的数值优化方法进行,这通常需要一阶或者导数,导数需要通过解析或者数值方法得到。
- 通过 期望最大化算法 的修改实现,这种方法不需要后验密度的导数。
尽管最大后验估计与贝叶斯统计共享先验分布的使用,通常并不认为它是一种贝叶斯方法,这是因为最大后验估计是点估计,然而贝叶斯方法的特点是使用这些分布来总结数据、得到推论。贝叶斯方法试图算出后验均值或者中值以及后验区间估计(posterior interval),而不是后验模。尤其是当后验分布没有一个简单的解析形式的时候更是这样:在这种情况下,后验分布可以使用马尔可夫链蒙特卡尔理论(Markov chain Monte Carlo)技术来模拟,但是找到它的模的优化是很困难或者是不可能的。
三、最小二乘法和最大似然估计
最小二乘法(英语:least squares
method),又称最小平方法,是一种数学优化方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
“最小二乘法”是对超定方程组,即方程个数比未知数更多的方程组,以回归分析求得近似解的标准方法。在这整个解决方案中,最小二乘法演算为每一方程式的结果中,将残差平方和的总和最小化。
最重要的应用是在曲线拟合上。最小平方所涵义的最佳拟合,即残差(残差为:观测值与模型提供的拟合值之间的差距)平方总和的最小化。当问题在自变量(x变量)有重大不确定性时,那么使用简易回归和最小二乘法会发生问题;在这种情况下,须另外考虑变量-误差-拟合模型所需的方法,而不是最小二乘法。
最小平方问题分为两种:线性或普通的最小二乘法,和非线性的最小二乘法,取决于在所有未知数中的残差是否为线性。线性的最小平方问题发生在统计回归分析中;它有一个封闭形式的解决方案。非线性的问题通常经由迭代细致化来解决;在每次迭代中,系统由线性近似,因此在这两种情况下核心演算是相同的。
最小二乘法所得出的多项式,即以拟合曲线的函数来描述自变量与预计应变量的变异数关系。
当观测值来自指数族且满足轻度条件时,最小平方估计和最大似然估计是相同的。最小二乘法也能从动差法得出。link
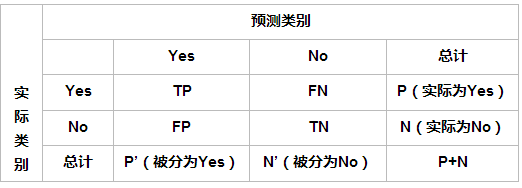
四、混淆矩阵
在机器学习领域和统计分类问题中,混淆矩阵(confusion matrix)是可视化工具,特别用于监督学习,在无监督学习一般叫做匹配矩阵。矩阵的每一列代表一个类的实例预测,而每一行表示一个实际的类的实例。之所以如此命名,是因为通过这个矩阵可以方便地看出机器是否将两个不同的类混淆了(比如说把一个类错当成了另一个)。
| 含义 | |
|---|---|
| TP | 真实类别为positive,模型预测的类别也为positive |
| FP | 预测为positive,但真实类别为negative,真实类别和预测类别不一致 |
| FN | 预测为negative,但真实类别为positive,真实类别和预测类别不一致 |
| TN | 真实类别为negative,模型预测的类别也为negative |
准确率(accuracy)计算公式如下所示: A C C = T P + T N T P + F N + F P + T N = T P + T N a l l d a t a ACC = \frac{TP + TN}{TP + FN + FP + TN} = \frac{TP + TN}{all \; data} ACC=TP+FN+FP+TNTP+TN=alldataTP+TN 在数据集不平衡时,准确率将不能很好地表示模型的性能。可能会存在准确率很高,而少数类样本全分错的情况,此时应选择其它模型评价指标。
精确率和召回率
| 公式 | |
|---|---|
| 精确率/查准率 | p r e c i s i o n = T P T P + F P = T P 预 计 为 p o s i t i v e 的 样 本 precision = \frac{TP}{TP + FP}=\frac{TP}{预计为positive的样本} precision=TP+FPTP=预计为positive的样本TP |
| 召回率/查全率 | r e c a l l = T P T P + F N = T P 真 值 为 p o s i t i v e 的 样 本 recall = \frac{TP}{TP + FN}=\frac{TP}{真值为positive的样本} recall=TP+FNTP=真值为positive的样本TP |
的精确率表示在预测为positive的样本中真实类别为positive的样本所占比例;召回率表示在真实为positive的样本中模型成功预测出的样本所占比例。
F 1 F_1 F1值和 F β F_\beta Fβ值
| 公式 | |
|---|---|
| F 1 F_1 F1 | F 1 = 2 ⋅ p r e c i s i o n ⋅ r e c a l l p r e c i s i o n + r e c a l l F_1 = \frac{2\cdot precision\cdot recall}{precision + recall} F1=precision+recall2⋅precision⋅recall |
| F β F_\beta Fβ | F β = ( 1 + β ) ⋅ p r e c i s i o n ⋅ r e c a l l β 2 ⋅ p r e c i s i o n + r e c a l l F_\beta = \frac{(1 + \beta)\cdot precision\cdot recall}{\beta^2\cdot precision + recall} Fβ=β2⋅precision+recall(1+β)⋅precision⋅recall |
注意:在 β = 1 \beta=1 β=1时, F β F_\beta Fβ就是 F 1 F_1 F1值,此时 F β F_\beta Fβ认为精确率和召回率一样重要;当 β > 1 \beta>1 β>1时, F β F_\beta Fβ认为召回率更重要;当 0 < β < 1 0<\beta<1 0<β<1时, F β F_\beta Fβ认为精确率更重要。除了 F 1 F_1 F1值之外,常用的还有 F 2 F_2 F2和 F 0.5 F_{0.5} F0.5
ROC曲线及其AUC值
AUC全称为Area Under Curve,表示一条曲线下面的面积,ROC曲线的AUC值可以用来对模型进行评价。ROC曲线下如图所示:

ROC曲线的纵坐标True Positive Rate(TPR)在数值上就等于positive class的recall,记作recallpositive,横坐标False Positive Rate(FPR)在数值上等于(1 - negative class的recall),记作(1 - r e c a l l n e g a t i v e recall_{negative} recallnegative)如下所示: T R P = T P T P + F N = r e c a l l p o s i t i v e TRP = \frac{TP}{TP + FN} = recall_{positive} TRP=TP+FNTP=recallpositive F P R = F P F P + T N = F P + T N T N F P + T N = 1 − T N F P + T N = 1 − r e c a l l n e g a t i v e FPR = \frac{FP}{FP + TN} = \frac{FP + TN _ TN}{FP + TN} \\= 1 - \frac{TN}{FP + TN} \\= 1 - recall_{negative} FPR=FP+TNFP=FP+TNFP+TNTN=1−FP+TNTN=1−recallnegative
通过对分类阈值 θ \theta θ(默认0.5)从大到小或者从小到大依次取值,我们可以得到很多组TPR和FPR的值,将其在图像中依次画出就可以得到一条ROC曲线,阈值 θ \theta θ取值范围为[0,1]。
ROC曲线在图像上越接近左上角(0,1)模型越好,即ROC曲线下面与横轴和直线FPR = 1围成的面积(AUC值)越大越好。直观上理解,纵坐标TPR就是 r e c a l l p o s i t i v e recall_{positive} recallpositive值,横坐标FPR就是(1 - r e c a l l n e g a t i v e recall_{negative} recallnegative),前者越大越好,后者整体越小越好,在图像上表示就是曲线越接近左上角(0,1)坐标越好。
上图展示了3个模型的ROC曲线,要知道哪个模型更好,则需要计算每条曲线的AUC值,一般认为AUC值越大越好。AUC值由定义通过计算ROC曲线、横轴和直线FPR = 1三者围成的面积即可得到。