凸包算法详解(Graham扫描法)

什么是凸包？

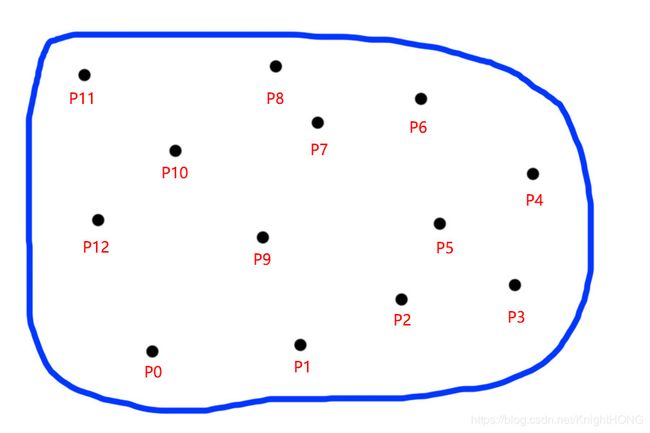
来打一个比方，假设我现在拿了一块木板，然后在上面无规则的随意钉上了几个钉子，并给他们命名为P0-P12，如下图所示：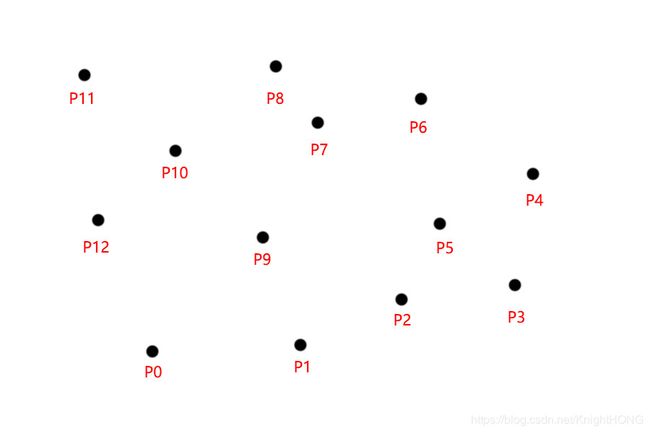

现在我拿了一根绳子，打了一个结，让绳子变成一个圆套，放在木板上并且让所有钉子都处在圆套内，如下图所示：

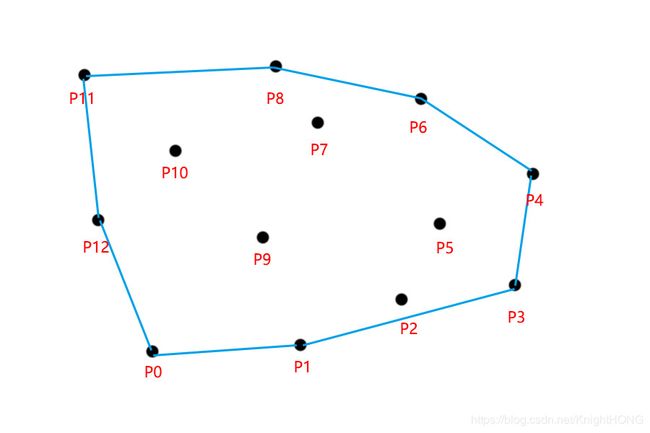
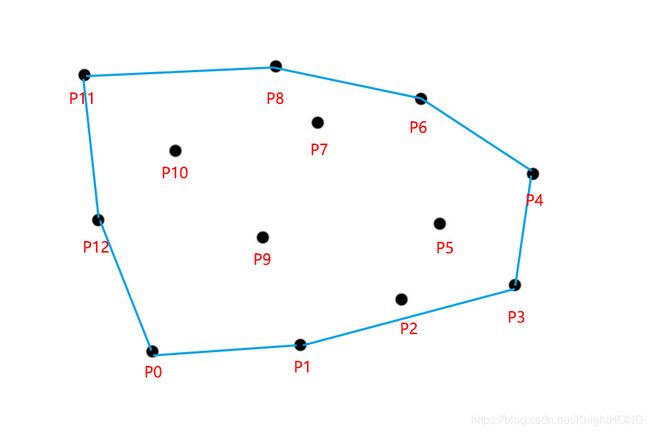
现在我要收缩圆套，让所有钉子都在圆套内且绳子的长度最短，大家觉得该如何去做才能实现上述所说呢？是的，就是把钉子中最外围的点连接成一条线，就能让所有的钉子在圆套内，并且绳子所需要的长度最短。如下图所示：

这类求解最外围的点集问题，我们称之为凸包问题，光光是用肉眼去观察的话，这种问题我们很快就能得出答案，并且能马上说出哪几个点是解，但是如果让你敲代码，去解决这类的问题，可能很多人会不知道如何去下手。

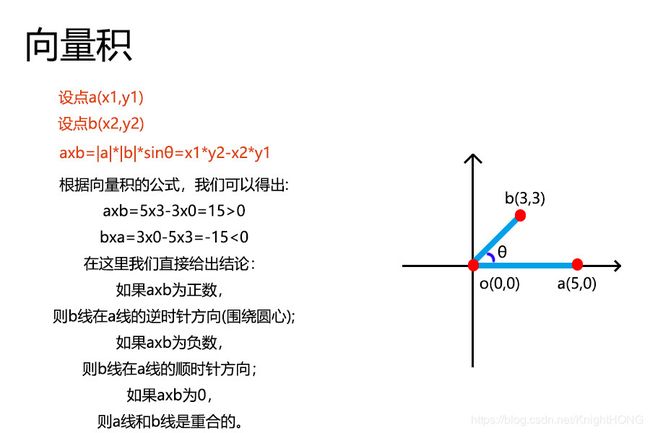
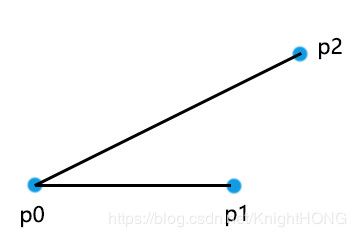
在讲解凸包这类问题的解法前，我们首先要先讲下向量积这个数学小知识。

了解了上面这个数学小知识后，我们现在可以正式开始着手去解决凸包问题了，首先我们先思考下，如果我们要去解决凸包问题，我们就必须要一个个去寻找最外围的点，万事开头难，第一个点该从哪里找起呢？

所有的点都在一个二维的平面上，细想一下，其中y轴（纵坐标）最小的点是不是我们要找的最外围的点之一呢？答案是肯定的，如果纵坐标最小的点有多个，那么我们就选取x轴（横坐标）最小的一个，如果这样的点也有多个也就是重合，也不影响解题。以此类推，其实也可以找纵坐标最大的点，还有横坐标最小的点，或者是横坐标最大的点作为基准点。这里呢，我们就以纵坐标最小的点作为我们的基准点，可以把它看作是原点。然后把剩下的点（除原点）进行排序，排序的方法为：把每个点与原点间进行连线，如果和水平线（x轴正半轴）的夹角越小，则排在越前面，我们叫这种排序法为极角排序。

排完序后如同上图所示，我们命名为p0~p8，p0就是我们一开始就找到的原点（纵坐标最小的点），p1是与p0连线与水平线（x轴正半轴）夹角最小的，往后p2,p3分别是夹角第二小，夹角第三小……。既然p0-p1这条直线是夹角最小的，那么p1点就是处于靠下的位置了，也就是我们要找的最外围的点之一了，从图中也能观察出这一点，反过来说，夹角最大的点p8也是最外围的点之一了，大家也可以尝试自己画出几个点来，也会得出这样一个结论。

观察上面这张图，当我们连接了p0和p1后，是不是所有符合凸包算法要找的点都往左边进行了不同程度的拐弯，p1-p3直线相对于p0-p1直线往左边拐了点，p3-p4直线相对于p1-p3直线向左边拐了点……，由此观察出，我们要找的点都必须向左拐弯，而不能向右拐弯，如果是向右拐弯，就说明这个点（两条线的连接点）应该在圆套内是被包围的点，而不是最外围的点。

知道了这个信息后，我们代码的编写就知道思路了。首先，刚开始的时候我们知道p0,p1这两个点，连接后，我们去找下一个点p2，如果p2是向左拐的我们就暂时把它算进我们最外围的点之一，然后去找p3这个点，然后发现p2-p3是在p1-p2的基础上向右转的，这说明中间这个点不是我们要找的点，我们就把存进去的p2删去，倒回到p1这个点，让p1去连接p3，如果p1-p3是在p0-p1基础上向左边拐，我们就把p3暂时算作我们要寻找的点之一，然后去寻找p4；如果不是，则把中间的点再次删去，倒回前一个点，如此往复，循环一边所有的点后得出的点集就是这个凸包问题的解。

如何判断是向右转还是向左转，就要用到我们刚刚教的数学小知识：向量积了。

上图这个p1-p2直线是满足向左转的条件的（相对于p0-p1直线），那么既然是向左转，那么这个p2这个点就一定在p0-p1直线的左边，也就有：

p0-p1直线的左边是p0-p2直线，所以现在我们只需要判断p0-p1和p0-p2这两条直线的向量积，如果是>0，p0-p2这条直线在p0-p1直线的逆时针方向（围绕p0点），也就是向左转；如果是<0，p0-p2这条直线则是在p0-p1直线的顺时针方向，也就是向右转；如果是=0，则是在同一条直线上。

好了，现在我们来练练手，来一道凸包算法的题目：（代码解释也会给出，在题目后面）

原题网址：http://acm.hdu.edu.cn/showproblem.php?pid=1392

 

Surround the Trees

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10299    Accepted Submission(s): 3991

 

Problem Description

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him? 
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.

There are no more than 100 trees.

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.

Zero at line for number of trees terminates the input for your program.

 

Output

The minimal length of the rope. The precision should be 10^-2.

 

Sample Input

9

12 7

24 9

30 5

41 9

80 7

50 87

22 9

45 1

50 7

0

 

Sample Output

243.06

 

代码编写：

 

struct Knight{
	int x;
	int y;
}p[maxn],s[maxn];

我们首先创建一个结构体数组p[maxn]，来存放题目输入的数据：x和y坐标。至于s[maxn]是用来存放我们最外围点集的。

int cross_product(Knight a,Knight b,Knight c){
	return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}

接下来这个函数要传进3个形参，也就是三个坐标，然后通过向量积来判断向左还是向右转，忘记了公式的童鞋可以回去再看看上面向量积的介绍哦。

double dis(Knight a,Knight b){
	return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y)*1.0);
}

这个函数是计算两点之间的距离。

int cmp1(Knight a,Knight b){
	if(a.y==b.y)
		return a.x

这个大家都经常写到的啦，用在排序里，意思是返回纵坐标较小的值，如果纵坐标相等，则返回横坐标较小的值。

int cmp2(Knight a,Knight b){
	int m = cross_product(s[0],a,b);
	if(m>0){
		return 1;
	}else if(m==0&&dis(s[0],a)-dis(s[0],b)<=0){
		return 1;
	}else{
		return 0;
	}
}

这个cmp2就是极角排序了，网上还有一种更快的排序方法，但是上面这个，我认为相对来说好理解点，大家可以先理解上面这个排序，理解完后，再理解下面这个，我也给出来了：

//x和y为找到的纵坐标最小坐标，即基准点（原点） 
int cmp2(Knight a,Knight b)
{
    if(atan2(a.y-y,a.x-x)!=atan2(b.y-y,b.x-x))
        return (atan2(a.y-y,a.x-x))<(atan2(b.y-y,b.x-x));
    return a.x

附上这道题的AC代码：算法复杂度O(nlogn)

#include 
#define ll long long 
using namespace std;
const int maxn = 1000;
struct Knight{
	int x;
	int y;
}p[maxn],s[maxn];

int cross_product(Knight a,Knight b,Knight c){
	return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}

double dis(Knight a,Knight b){
	return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y)*1.0);
}

int cmp1(Knight a,Knight b){
	if(a.y==b.y)
		return a.x0){
		return 1;
	}else if(m==0&&dis(s[0],a)-dis(s[0],b)<=0){
		return 1;
	}else{
		return 0;
	}
}
/*
//x和y为找到的纵坐标最小坐标，即基准点（原点） 
int cmp2(Knight a,Knight b)
{
    if(atan2(a.y-y,a.x-x)!=atan2(b.y-y,b.x-x))
        return (atan2(a.y-y,a.x-x))<(atan2(b.y-y,b.x-x));
    return a.x