SVM——(三)对偶性和KKT条件(Lagrange duality and KKT condition)
之前说到过拉格朗日乘数法以及推导过程,那么今天要说的就是拉格朗日对偶性以及KKT条件
1.Lagrange multipliers
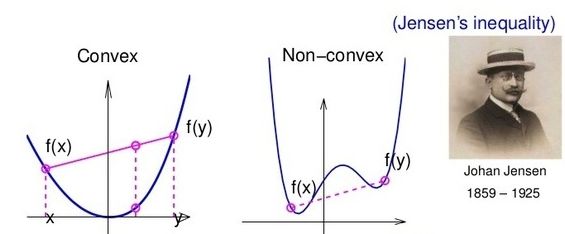
一句话说,拉格朗日乘数法就是用来解决条件极值的一个方法,且约束条件都是等式(equality)的形式;由拉格朗日乘数法通常用来解决一些凸优化(convex optimization)问题,所以一般情况下求解的都是极小值,即 min ω f ( ω ) \min_{\omega} f(\omega) minωf(ω)
顺便说一句,convex function 的图像如下:
请看下面这个优化问题:
min ω f ( ω ) s . t . h i ( ω ) = 0 , i = 1 , ⋯ , l . \begin{aligned} \min_{\omega} \;\;\;f(\omega)&\\ s.t. \;\;\;h_i(\omega)&=0,i=1, \cdots,l. \end{aligned} ωminf(ω)s.t.hi(ω)=0,i=1,⋯,l.
其中 ω 是 一 个 向 量 \omega是一个向量 ω是一个向量;很明显这是一个条件(等式)极值问题,且用拉格朗日乘数法就能解决。
L a n g r a n g i a n \bf{Langrangian} Langrangian
L ( ω , β ) = f ( ω ) + ∑ i = 1 l β i h i ( ω ) \mathcal{L}(\omega,\beta) = f(\omega)+\sum^l_{i=1}\beta_ih_i(\omega) L(ω,β)=f(ω)+i=1∑lβihi(ω)
其中 β i \beta_i βi是拉格朗日乘子;然后对式子中所有的参数求偏导,令其为0(推导)求解出所有参数;
∂ L ∂ ω i = 0 ; ∂ L ∂ β i = 0 \frac{\partial\mathcal{L}}{\partial\omega_i}=0;\;\;\;\frac{\partial\mathcal{L}}{\partial\beta_i}=0 ∂ωi∂L=0;∂βi∂L=0
2.Generalized Lagrangian
请看如下优化问题:
min ω f ( ω ) s . t . g i ( ω ) ≤ 0 , i = 1 , ⋯ , k . h i ( ω ) = 0 , i = 1 , ⋯ , l . (01) \begin{aligned} \min_{\omega} \;\;\;f(\omega)&\tag {01}\\ s.t. \;\;\;g_i(\omega)&\leq0,i=1, \cdots,k.\\[2ex] h_i(\omega)&=0,i=1, \cdots,l. \end{aligned} ωminf(ω)s.t.gi(ω)hi(ω)≤0,i=1,⋯,k.=0,i=1,⋯,l.(01)
与之前明显不同的就是多了不等式的约束条件;为了解决这个问题,下面我们就要定义广义的拉格朗日乘数法(Generalized Lagrangian)。
G e n e r a l i z e d L a g r a n g i a n \bf{Generalized Lagrangian} GeneralizedLagrangian
L ( ω , α , β ) = f ( ω ) + ∑ i = 1 k α i g i ( ω ) + ∑ i = 1 l β i h i ( ω ) (02) \mathcal{L}(\omega,\alpha,\beta) = f(\omega)+\sum^k_{i=1}\alpha_ig_i(\omega)+\sum^l_{i=1}\beta_ih_i(\omega)\tag {02} L(ω,α,β)=f(ω)+i=1∑kαigi(ω)+i=1∑lβihi(ω)(02)
其中 α i \alpha_i αi和 β i \beta_i βi都是拉格朗日乘子;接下来就是进行求解,然而求解方法却与之前大相径庭了。
3.Primal and dual optimization problem
3.1 Primal optimization problem
定义:
θ p ( ω ) = max α , β : α i ≥ 0 L ( ω , α , β ) (03) \theta_p(\omega)=\max_{\alpha,\beta:\alpha_i\geq0}\mathcal{L}(\omega,\alpha,\beta)\tag {03} θp(ω)=α,β:αi≥0maxL(ω,α,β)(03)
这个式子表示的含义是:求 L ( ω , α , β ) \mathcal{L}(\omega,\alpha,\beta) L(ω,α,β)的最大值, α , β \alpha,\beta α,β作为自变量(与 ω \omega ω无关),求得的结果 θ p \theta_p θp是关于 ω \omega ω的函数
我们现在来做这样一个假设,存在 g i g_i gi或 h i h_i hi使得原约束条件不成立,即( g i ( ω ) > 0 o r h i ( ω ) ≠ 0 g_i(\omega)>0\;or\;h_i(\omega)\ne0 gi(ω)>0orhi(ω)=0),如果是这样的话 θ p \theta_p θp会发生什么变化呢?
如果 g i ( ω ) > 0 g_i(\omega)>0 gi(ω)>0,为了求得 L \mathcal{L} L的最大值,只需要取 α i \alpha_i αi为无穷大,则此时 L \mathcal{L} L最大,但又没有意义;同样,如果 h i ( ω ) ≠ 0 h_i(\omega)\neq0 hi(ω)=0,取 β \beta β为无穷大( h i h_i hi与 β \beta β同号),则同样会无穷大。于是我们就会得到下面这个式子:
θ p ( ω ) = { f ( ω ) , if ω satisfies primal constraints ∞ , otherwise (04) \theta_p(\omega) = \begin{cases} f(\omega), & \text{if $\omega$ satisfies primal constraints} \\[2ex] \infty, & \text{otherwise} \end{cases}\tag {04} θp(ω)=⎩⎨⎧f(ω),∞,if ω satisfies primal constraintsotherwise(04)
因此, θ p ( ω ) \theta_p(\omega) θp(ω)就等同于 f ( ω ) f(\omega) f(ω)了,再进一步 min θ p ( ω ) \min \theta_p(\omega) minθp(ω)就等同于原问题(1)了。于是我们就有如下定义:
p ∗ = min w θ p ( ω ) = min w max α , β : α i ≥ 0 L ( ω , α , β ) (05) p^*=\min_{w}\theta_p(\omega)=\min_{w}\max_{\alpha,\beta:\alpha_i\geq0}\mathcal{L}(\omega,\alpha,\beta)\tag {05} p∗=wminθp(ω)=wminα,β:αi≥0maxL(ω,α,β)(05)并将其称之为原始优化问题(Primal optimization problem)
仔细想想可以知道: 把(3)式改为 θ p = min α , β : α i < 0 L ( ω , α , β ) \theta_p=\min_{\alpha,\beta:\alpha_i<0}\mathcal{L}(\omega,\alpha,\beta) θp=minα,β:αi<0L(ω,α,β)同样等同于 f ( ω ) f(\omega) f(ω),且 min w θ p ( ω ) \min_{w}\theta_p(\omega) minwθp(ω)等同于(1);但是如果这样做的话 min min L \min\min\mathcal{L} minminL才等价于原问题,就不能采用对偶性来求解原问题了。
3.2 Dual optimization problem
定义:
θ d ( α , β ) = min ω L ( ω , α , β ) (06) \theta_d(\alpha,\beta)=\min_{\omega}\mathcal{L}(\omega,\alpha,\beta)\tag {06} θd(α,β)=ωminL(ω,α,β)(06)
这个式子表示的含义是:求 L ( ω , α , β ) \mathcal{L}(\omega,\alpha,\beta) L(ω,α,β)的最小值, ω \omega ω作为自变量(与 α , β \alpha,\beta α,β无关),求得的结果 θ d \theta_d θd是关于 α , β \alpha,\beta α,β的函数。
此时,我们就能定义出原问题的对偶问题了:
d ∗ = max α , β : α i ≥ 0 θ d ( α , β ) = max α , β : α i ≥ 0 min ω L ( ω , α , β ) (07) d^*=\max_{\alpha,\beta:\alpha_i\geq0}\theta_d(\alpha,\beta)=\max_{\alpha,\beta:\alpha_i\geq0}\min_{\omega}\mathcal{L}(\omega,\alpha,\beta)\tag {07} d∗=α,β:αi≥0maxθd(α,β)=α,β:αi≥0maxωminL(ω,α,β)(07)
并将其称之为对偶优化问题(Dual optimization problem)
那么原始问题和对偶问题有什么关系呢? 我们为什么又要用对偶问题?通常情况下两者满足以下关系:
d ∗ = max α , β : α i ≥ 0 min ω L ( ω , α , β ) ≤ min w max α , β : α i ≥ 0 L ( ω , α , β ) = p ∗ (08) d^*=\max_{\alpha,\beta:\alpha_i\geq0}\min_{\omega}\mathcal{L}(\omega,\alpha,\beta)\leq\min_{w}\max_{\alpha,\beta:\alpha_i\geq0}\mathcal{L}(\omega,\alpha,\beta)=p^*\tag {08} d∗=α,β:αi≥0maxωminL(ω,α,β)≤wminα,β:αi≥0maxL(ω,α,β)=p∗(08)
证明:
由(03),(06)可知,对于任意的 ω , α , β \omega,\alpha,\beta ω,α,β有
θ d ( α , β ) = min ω L ( ω , α , β ) ≤ L ( ω , α , β ) ≤ max α , β : α i ≥ 0 L ( ω , α , β ) = θ p ( ω ) \theta_d(\alpha,\beta)=\min_{\omega}\mathcal{L}(\omega,\alpha,\beta)\leq\mathcal{L}(\omega,\alpha,\beta)\leq\max_{\alpha,\beta:\alpha_i\geq0}\mathcal{L}(\omega,\alpha,\beta)=\theta_p(\omega) θd(α,β)=ωminL(ω,α,β)≤L(ω,α,β)≤α,β:αi≥0maxL(ω,α,β)=θp(ω)
由不等式的传递性可知:
θ d ( α , β ) ≤ θ p ( ω ) \theta_d(\alpha,\beta)\leq\theta_p(\omega) θd(α,β)≤θp(ω)
由于原始问题和对偶问题均有最优值,所以:
max α , β : α i ≥ 0 θ d ( α , β ) ≤ min w θ p ( ω ) \max_{\alpha,\beta:\alpha_i\geq0}\theta_d(\alpha,\beta)\leq\min_{w}\theta_p(\omega) α,β:αi≥0maxθd(α,β)≤wminθp(ω)
即:
θ d ( α , β ) = min ω L ( ω , α , β ) ≤ L ( ω , α , β ) ≤ max α , β : α i ≥ 0 L ( ω , α , β ) = θ p ( ω ) \theta_d(\alpha,\beta)=\min_{\omega}\mathcal{L}(\omega,\alpha,\beta)\leq\mathcal{L}(\omega,\alpha,\beta)\leq\max_{\alpha,\beta:\alpha_i\geq0}\mathcal{L}(\omega,\alpha,\beta)=\theta_p(\omega) θd(α,β)=ωminL(ω,α,β)≤L(ω,α,β)≤α,β:αi≥0maxL(ω,α,β)=θp(ω)
而之所以要用对偶问题是因为直接对原始问题进行求解异常困难,所以一般将其转转换为对偶问题进行求解。但就目前来看,两者并不等同,其解也就必然不会相同。所以下面就要说到KKT条件了。
4.KKT conditions
上面说到,要想用对偶问题的解来代替原始问题的解,就必须使得两者等价;对于原始问题和对偶问题,假设函数 f ( ω ) f(\omega) f(ω)和 h i ( ω ) h_i(\omega) hi(ω)是凸函数, h i ( ω ) h_i(\omega) hi(ω)是仿射函数,且不等式 g i ( ω ) g_i(\omega) gi(ω)严格可行(对于所有的i都有 g i ( ω ) < 0 g_i(\omega)<0 gi(ω)<0),则 ω ∗ \omega^* ω∗和 α ∗ , β ∗ \alpha^*,\beta^* α∗,β∗分别是原始问题和对偶问题的解的充分必要条件是 ω ∗ , α ∗ , β ∗ \omega^*,\alpha^*,\beta^* ω∗,α∗,β∗满足 Karush-Kuhn-Tucker(KKT) 条件:
∂ ∂ α i L ( ω ∗ , α ∗ , β ∗ ) = 0 , i = 1 , ⋯ , k (09) \begin{aligned} \frac{\partial}{\partial\alpha_i}\mathcal{L}(\omega^*,\alpha^*,\beta^*)=0,i=1,\cdots,k\tag {09} \end{aligned} ∂αi∂L(ω∗,α∗,β∗)=0,i=1,⋯,k(09)
∂ ∂ ω i L ( ω ∗ , α ∗ , β ∗ ) = 0 , i = 1 , ⋯ , n (10) \begin{aligned} \frac{\partial}{\partial\omega_i}\mathcal{L}(\omega^*,\alpha^*,\beta^*)=0,i&=1,\cdots,n\tag {10} \end{aligned} ∂ωi∂L(ω∗,α∗,β∗)=0,i=1,⋯,n(10)
∂ ∂ β i L ( ω ∗ , α ∗ , β ∗ ) = 0 , i = 1 , ⋯ , l (11) \begin{aligned} \frac{\partial}{\partial\beta_i}\mathcal{L}(\omega^*,\alpha^*,\beta^*)=0,i&=1,\cdots,l\tag {11} \end{aligned} ∂βi∂L(ω∗,α∗,β∗)=0,i=1,⋯,l(11)
α i ∗ g i ( ω ∗ ) = 0 , i = 1 , ⋯ , k (12) \begin{aligned} \alpha_i^*g_i(\omega^*)=0,i&=1,\cdots,k \tag{12} \end{aligned} αi∗gi(ω∗)=0,i=1,⋯,k(12)
g i ( ω ∗ ) ≤ 0 , i = 1 , ⋯ , k (13) \begin{aligned} g_i(\omega^*)\leq0,i&=1,\cdots,k\tag{13} \end{aligned} gi(ω∗)≤0,i=1,⋯,k(13)
α i ∗ ≥ 0 , i = 1 , ⋯ , k (14) \begin{aligned} \alpha_i^*\geq0,i&=1,\cdots,k\tag{14} \end{aligned} αi∗≥0,i=1,⋯,k(14)
其中(12)称为KKT的对偶互补条件(dual complementarity condition),由此可知,如果 α i ∗ > 0 \alpha^*_i>0 αi∗>0则有 g i ( ω ) = 0 g_i(\omega)=0 gi(ω)=0,而这一点也将用来说明SVM仅仅只有特别少的"支持向量"(support vectors)
注: h ( x ) h(x) h(x)称为放射函数,如果它满足 h ( x ) = α ⋅ x + b , α ∈ R n , b ∈ R , x ∈ R n h(x)=\alpha\cdot x+b,\alpha\in R^n,b\in R,x\in R^n h(x)=α⋅x+b,α∈Rn,b∈R,x∈Rn
若原始问题和对偶问题都有最优值,则:
d ∗ = max α , β : α i ≥ 0 min ω L ( ω , α , β ) = min w max α , β : α i ≥ 0 L ( ω , α , β ) = p ∗ (15) d^*=\max_{\alpha,\beta:\alpha_i\geq0}\min_{\omega}\mathcal{L}(\omega,\alpha,\beta)=\min_{w}\max_{\alpha,\beta:\alpha_i\geq0}\mathcal{L}(\omega,\alpha,\beta)=p^*\tag {15} d∗=α,β:αi≥0maxωminL(ω,α,β)=wminα,β:αi≥0maxL(ω,α,β)=p∗(15)
5.Example
求解以下优化问题:
min x f ( x ) = x 1 2 + x 2 2 s. t. h ( x ) = x 1 − x 2 − 2 = 0 g ( x ) = ( x 1 − 2 ) 2 + x 2 2 − 1 ≤ 0 (16) \begin{array}{ll} \min_{\boldsymbol{x}} & f(\boldsymbol{x})=x_1^2+x_2^2\\ \textrm{s. t.} & h(\boldsymbol{x})=x_1-x_2-2=0\\ ~ & g(\boldsymbol{x}) = (x_1-2)^2+x_2^2 -1\leq 0\\ \tag{16}\end{array} minxs. t. f(x)=x12+x22h(x)=x1−x2−2=0g(x)=(x1−2)2+x22−1≤0(16)
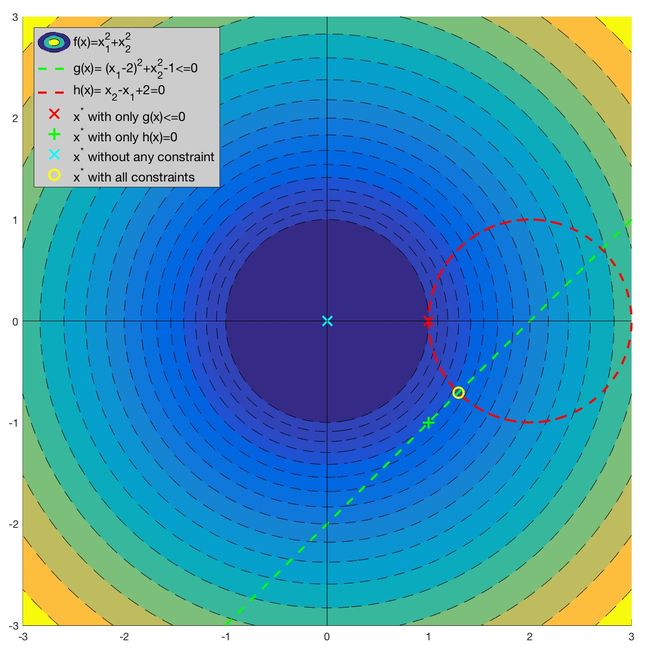
由于优化问题 ( 16 ) (16) (16)相对简单,我们可以先通过作图来直观感受以下:(点击可放大)
之所以说这个案例比较典型是因为它与线性SVM的数学模型非常相似,且包含了等式和不等式两种不同的约束条件。更重要的是,这两个约束条件在优化问题中都起到了作用。如图所示(左上角所示):
- 如果没有任何约束条件,最优解在坐标原点(0, 0)处(青色X);
- 如果只有不等式约束条件 g ( x ) ≤ 0 g(\boldsymbol{x})\leq 0 g(x)≤0,最优解在坐标(1,0)处(红色x);
- 如果只有等式约束条件 h ( x ) = 0 h(\boldsymbol{x})=0 h(x)=0 ,最优解在坐标(1,-1)处(绿色+);
- 如果两个约束条件都有,最优解在 ( 2 − 2 / 2 , − 2 / 2 ) (2-\sqrt{2}/2,-\sqrt{2}/2) (2−2/2,−2/2) 处(黄色O)。
针对这一问题,我们可以设计拉格朗日函数如下:
L ( x , α , β ) = ( x 1 2 + x 2 2 ) + α [ ( x 1 − 2 ) 2 + x 2 2 − 1 ] + β ( x 1 − x 2 − 2 ) (17) L(\boldsymbol{x},\alpha,\beta)=(x_1^2+x_2^2)+\alpha\left[(x_1-2)^2+x_2^2-1\right]+\beta(x_1-x_2-2)\tag{17} L(x,α,β)=(x12+x22)+α[(x1−2)2+x22−1]+β(x1−x2−2)(17)
根据公式 ( 03 ) (03) (03)可知:
θ p ( x ) = max α , β : α ≥ 0 L ( x , α , β ) (18) \theta_p(x)=\max_{\alpha,\beta:\alpha\geq0}\mathcal{L}(x,\alpha,\beta)\tag{18} θp(x)=α,β:α≥0maxL(x,α,β)(18)
此时,我们依然可以得到,如果 x x x不满足上面的两个约束条件,即:
- 若 g ( x ) > 0 g(x)>0 g(x)>0;则可以任取 α \alpha α使得 θ p ( x ) \theta_p(x) θp(x)趋于无穷;
- 若 h ( x ) ≠ 0 h(x)\neq0 h(x)=0;则只有任取 β \beta β,且 β , h ( x ) \beta,h(x) β,h(x)同号,那么 θ p ( x ) \theta_p(x) θp(x)依旧可能趋于无穷;
- 而只有两个约束条件同时满足, θ p ( x ) \theta_p(x) θp(x)才可能取到最大值;
于是有
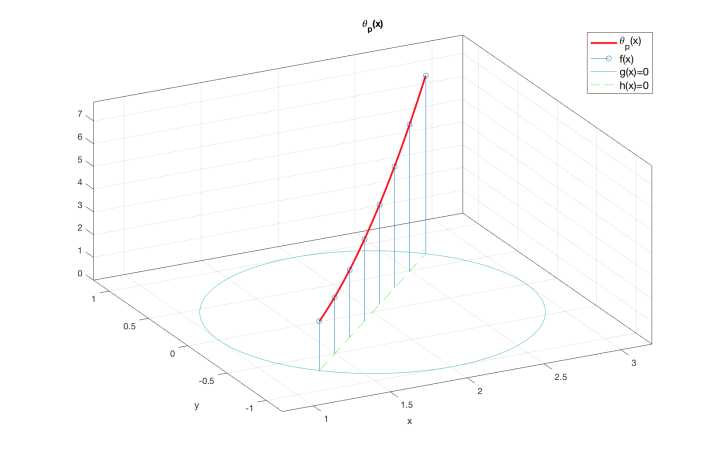
θ p ( x ) = { f ( x ) , if x satisfies primal constraints ∞ , otherwise (19) \begin{aligned} \theta_p(x) = \begin{cases} f(x), & \text{if $x$ satisfies primal constraints} \\[2ex] \infty, & \text{otherwise} \end{cases}\tag{19} \end{aligned} θp(x)=⎩⎨⎧f(x),∞,if x satisfies primal constraintsotherwise(19)
且如图所示:函数 θ p ( x ) \theta_p(\boldsymbol{x}) θp(x) 只在绿色直线在红色圆圈内的部分——也就是直线 h ( x ) = 0 h(\boldsymbol{x})=0 h(x)=0在圆 g ( x ) = 0 g(\boldsymbol{x})=0 g(x)=0上的弦——与原目标函数 f ( x f(\boldsymbol{x} f(x 取相同的值,而在其他地方均有 θ P ( x ) = + ∞ \theta_P(\boldsymbol{x})=+\infty θP(x)=+∞
故,其原始问题为:
p ∗ = min x max α , β : α > 0 L ( x , α , β ) (20) p^*=\min_{x}\max_{\alpha,\beta:\alpha>0}\mathcal{L}(x,\alpha,\beta)\tag{20} p∗=xminα,β:α>0maxL(x,α,β)(20)
此处本应该先验证KKT条件是否成立,但说实话,此时对于KKT条件依旧有点模糊,感觉上面的笔记都是依样画葫芦;所以暂时就先不验证,等弄清楚再来补上。不过这样依然不影响我们求解。
那么其对偶问题就应该为:
d ∗ = max α , β : α > 0 min x L ( x , α , β ) (21) d^*=\max_{\alpha,\beta:\alpha>0}\min_{x}\mathcal{L}(x,\alpha,\beta)\tag{21} d∗=α,β:α>0maxxminL(x,α,β)(21)
对于求解对偶问题,一般分为两步:
- 最小化 L ( x , α , β ) \mathcal{L}(x,\alpha,\beta) L(x,α,β);
我们将 α , β \alpha,\beta α,β视为常数,这时 L ( x , α , β ) L(\boldsymbol{x},\alpha,\beta) L(x,α,β) 就只是 x \boldsymbol{x} x的函数。我们可以通过求导等于零的方式寻找其最小值,即 θ D ( α , β ) = min x [ L ( x , α , β ) ] \theta_D(\alpha,\beta)=\min_{\boldsymbol{x}}\left[L(\boldsymbol{x},\alpha,\beta)\right] θD(α,β)=minx[L(x,α,β)]
{ β + 2 x 1 + α ( 2 x 1 − 4 ) = 0 2 x 2 − β + 2 α x 2 = 0 (22) \left\{\begin{array}{l} \beta + 2x_1 + \alpha (2x_1 - 4)=0\\ 2x_2 - \beta + 2\alpha x_2=0 \end{array}\right.\tag{22} {β+2x1+α(2x1−4)=02x2−β+2αx2=0(22)
可以解得:
{ x 1 = 4 α − β 2 α + 2 x 2 = β 2 α + 2 (23) \left\{ \begin{array}{l} x_1 = \frac{4\alpha-\beta}{2\alpha + 2}\\ x_2 = \frac{\beta}{2\alpha + 2} \end{array}\right.\tag{23} {x1=2α+24α−βx2=2α+2β(23)
将 ( 22 ) (22) (22)代入拉格朗日目标函数 ( 17 ) (17) (17)可以得到:
θ D ( α , β ) = − β 2 + 4 β + 2 α 2 − 6 α 2 ( α + 1 ) (24) \theta_D(\alpha,\beta)= -\frac{\beta^2 + 4\, \beta + 2\, \alpha^2 - 6\, \alpha}{2\, \left(\alpha + 1\right)}\tag{24} θD(α,β)=−2(α+1)β2+4β+2α2−6α(24)
2. 最大化 θ D ( α , β ) \theta_D(\alpha,\beta) θD(α,β)
此时可以将 θ D ( α , β ) \theta_D(\alpha,\beta) θD(α,β)看成是一个二元函数求极值(无条件)的问题,且 α > 0 \alpha>0 α>0。用拉格朗日乘数法即可求解。
设 D = θ D ( α , β ) D=\theta_D(\alpha,\beta) D=θD(α,β),则 D D D分别对 α , β \alpha,\beta α,β求偏导并令其为0有:
∂ D ∂ α = − 2 α 2 + 4 α − β 2 − 4 β − 6 2 ( α + 1 ) 2 = 0 ; ∂ D ∂ β = 2 β + 4 2 ( α + 1 ) = 0 \begin{aligned} \frac{\partial D}{\partial\alpha}=-\frac{2\alpha^2+4\alpha-\beta^2-4\beta-6}{2(\alpha+1)^2}=0;\frac{\partial D}{\partial\beta}=\frac{2\beta+4}{2(\alpha+1)}=0 \end{aligned} ∂α∂D=−2(α+1)22α2+4α−β2−4β−6=0;∂β∂D=2(α+1)2β+4=0
联立求得:
α = 2 − 1 ( > 0 ) , β = − 2 \alpha=\sqrt{2}-1(>0),\beta=-2 α=2−1(>0),β=−2
再代入 ( 23 ) (23) (23)即可求得 x x x
由于在这个问题中,第二步求解相对简单所以可以用拉格朗日乘数法来做。但在大多数时候都将用到SMO来求解。
遇到不同问题的时候,注意弄清楚每个字母所表示的意义
SVM——(七)SMO(序列最小最优算法)
SVM——(六)软间隔目标函数求解
SVM——(五)线性不可分之核函数
SVM——(四)目标函数求解
SVM——(三)对偶性和KKT条件(Lagrange duality and KKT condition)
SVM——(二)线性可分之目标函数推导方法2
SVM——(一)线性可分之目标函数推导方法1
参考:
- https://zhuanlan.zhihu.com/p/24638007
- Andrew Ng. CS229. Note3
- 支持向量机通俗导论(理解SVM的三层境界)
- 《统计学习方法》