Andrew Ng - SVM【2】一步步迈向核函数——拉格朗日、原问题与对偶问题

Andrew Ng - SVM【2】一步步迈向核函数

---

1. 拉格朗日对偶规划

暂且撇开SVM和最大间隔分类器不管（当然不是真的不管），我们先来讨论一个在一定约束条件下的优化问题：

minωf(ω)s.t.hi(ω)=0,i=1,...,l

则该问题对应的拉格朗日函数为：

L(ω,β)=f(ω)+∑li=1βihi(ω)

βi 我们叫做拉格朗日乘数，接着我们令 L 偏导为零：

∂L∂ωi=0;∂L∂βi=0,

便可以求出 ω 和 β 。
对于更一般化的约束问题，除了等式约束条件以外，我们还要加入不等式约束条件，称之为 原问题，表达式如下：

minωf(ω)s.t.gi(ω)≤0,i=1,...,k   hi(ω)=0,i=1,...,l

该问题对应的拉格朗日函数为：

L(ω,α,β)=f(ω)+∑ki=1αigi(ω)+∑li=1βihi(ω)

αi 和 βi 我们叫做拉格朗日乘数，假设有如下等式：

θP(ω)=maxα,β:αi≥0L(ω,α,β).

这里下标 P 用来指代原优化问题。给定一些 ω ，如果 ω 违反了拉格朗日的任意约束条件（存在 gi(ω)>0 或者 hi(ω)≠0 ）， θP(ω)=∞ ；相反，如果所有约束条件满足，则 θP(ω)=f(ω) 。因此：

θP(ω)={f(ω)∞ω符合约束条件其他.

所以当我们需要最小化（为什么是最小化？后边会有答案） θP(ω) 的时候，即：

minwθP(ω)=minwmaxα,β:αi≥0L(ω,α,β).

为什么要最小化呢，因为最小化 θP(ω) 是我们的 原问题（如果你还记得 minωf(ω) ）。为了方便后边的使用，我们这里令 p∗=minwθP(ω) ，并称之为 原优化问题。
然后我们来看另一个问题，定义：

θD(α,β)=minωL(ω,α,β).

在原优化问题中，我们求的是 α,β 为参函数的最大值，而在 对偶问题（见上式）中，我们是对以 ω 为参的式子求最小值，其对应的 对偶优化问题为：

maxα,β:αi≥0θD(α,β)=maxα,β:αi≥0minωL(ω,α,β).

很明显除了 min 和 max 的顺序之外，原优化问题和对偶优化问题长得是一模一样。对于对偶优化问题，我们定义 d∗=maxα,β:αi≥0θD(ω) 。到这一步，大家肯定都很奇怪我们上边做了那么多是为了什么， d∗ 和 p∗ 有关系吗？下边就是关系！

d∗=maxα,β:αi≥0minωL(ω,α,β)≤minwmaxα,β:αi≥0L(ω,α,β)=p∗.

而且，在一些 特定的条件（KKT条件，这个可以参见凸优化问题的相关资料自行了解）下，我们甚至可以得到 d∗=p∗ ，所以我们可以将求解原优化问题转化为求解对偶优化问题。

2. KKT条件

假设 f 和 gi 都是凸函数， hi 是仿射函数，进一步假设 gi 是可执行的；也就是存在 ω 使所有的 gi<0 。在上述假设都满足的情况下，必然会有一些奇葩的事情要发生。 ω∗ 为原最优问题的解； α∗,β∗ 为对偶优化问题的解；而且 p∗=d∗=L(ω∗,α∗,β∗) ；而且 ω∗,α∗,β∗ 满足Karush-Kuhn-Tucker(KKT)条件：

∂L(ω∗,α∗,β∗)∂ωi=0,i=1,...,n∂L(ω∗,α∗,β∗)∂βi=0,i=1,...,lα∗igi(ω∗)=0,i=1,...,kgi(ω∗)≤0,i=1,...,k   α∗≥0,i=1,...,k

如果 ω∗,α∗,β∗ 满足KKT，那么 ω∗,α∗,β∗ 为原优化问题和对偶优化问题的解。注意标红的条件我们称之为 KKT对偶互补条件，其告诉我们，如果 α∗i>0 ，则 gi(ω)=0 ，这个点将是我们稍后认识SVM中支撑向量的钥匙；也是之后SMO算法在收敛测试时的一个重要条件。

3. 最优间隔分类器

在前面的篇幅中，为了寻找最优间隔分类器，我们提出了如下的原优化问题：

minγ,ω,b12||ω||2s.t.y(i)(ωTx(i)+b)≥1,i=1,...,m

为了描述问题，我们把约束条件改写一下：

gi(ω)=−y(i)(ωTx(i)+b)+1≤0

在讨论KKT互补条件的时候，我们说过只有在 gi(ω)=0 （即函数间隔为1）的时候 αi>0 ，那么看下图：



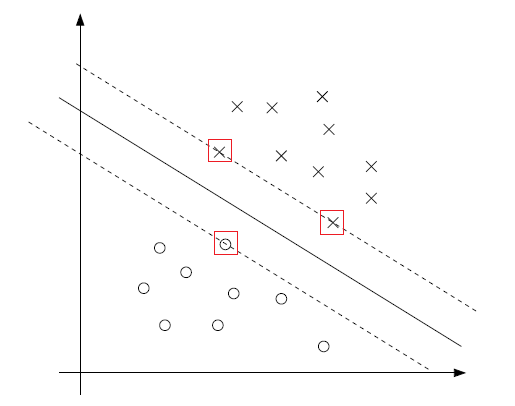
实线是最大间隔分割超平面。而有最小间隔的点应该是离超平面最近的点（函数间隔为1）；这样的点图上有三个（画圈的）。所以只有这三个点对应的 gi(ω)=0 ，相应的，也只有这三个点对应的 αi>0 ，我们称这样的点为 支撑向量（实际上就是落在函数间隔为1的超平面上的样本点）。由图上清晰可见支撑向量的数量相对于整个训练集实际上是很少的。
引入点积 ⟨x(i),x(j)⟩ ,即 (x(i))Tx(j) 的另一种写法，因为这种写法将让我们认识到什么叫做核方法！mark一下。然后构建优化问题的拉格朗日函数：

L(ω,b,α)=12||ω||2−∑mi=1αi[y(i)((ω)Tx(i)+b)−1]

因为优化问题中只有不等式约束条件，所以拉格朗日函数中只有 αi 而没有 βi 。那么该问题的对偶形式是什么呢？为给出对偶形式，我们先关于 ω 和 b 最小化 L(ω,b,α) ，即先关于 ω 求 L 的偏导：

∇ωL(ω,b,α)=ω−∑mi=1αiy(i)x(i)=0

由此可以得出：

ω=∑mi=1αiy(i)x(i)

再关于 b 求 L 的偏导：

∂L(ω,b,α)∂b=∑mi=1αiy(i)=0

将得到的 ω 的等式带回原问题并化简，我们可以得到原问题的 对偶优化问题：

maxαW(α)=∑i=1mαi−12∑i,j=1my(i)y(j)α(i)α(j)⟨x(i),x(j)⟩. s.t.αi≥0,i=1,...,m   ∑i=1mαiy(i)=0

实际上，可以证明我们的优化问题满足 d∗=p∗ 需要的条件，同时也满足KKT条件，因此我们可以通过求解对偶优化问题来求解原优化问题。而且明显可以看出我们上述的对偶优化问题是一个以 αi 为参的函数最大值的求解问题。 α 都求出来，问题解决！NO！暂且让我们把求 α 的高端算法放一放。假设已经求得了所要优化问题的 α ，因为 y(i) 和 x(i) 都是已知的，所以我们很轻松的搞定 ω ，在得到 ω∗ 之后，截距 b∗ 的求法如下：

b∗=−maxi:y(i)=1ω∗Tx(i)2.

为了进一步给核函数铺垫一下，对于上边绿色的求 ω 的式子我有话说！假设我们用一个训练集训练了这个模型，现在要去预测一个新的点 x ，计算 ωT+b ，如果大于1则 y=1 。 但是！但是！通过绿色的等式，这玩意还可以这样预测：

ωT+b=(∑i=1mαiy(i)x(i))Tx+b =∑i=1mαiy(i)⟨x(i),x⟩+b.

为什么要有 内积的出现呢？留一手！注意上边的式子中，记得我们曾提起过一个概念叫支撑向量，对于上边的式子来说，除了支撑向量对应的 αi 以外，其他的 αi 均为 0，而支撑向量又比较 少！！！求和中的许多项都 为0！！！这就很大程度上减少了我们的计算量。关于内积，其实是核函数中极为重要的一环，而通过核函数，可以提高我们的计算效率（即使在 高维甚至无限维）。