SVM用于手写数字识别

SVM用于手写数字识别

---

要求：指定只用SVM二分类： 数字5 against all

数据来源：http://archive.ics.uci.edu/ml/

---

SVM 我就不描述了。可以去问一个叫百度的人。

---

首先，对于所给的数据先不进行任何数据处理:

直接使用朴素特征进行SVM分类。

使用python语言实现。调用sklearn中的SVM
核函数选择：“RBF”
参数gamma 为核函数RBF参数Sigma的倒数。
    sklearn库文档说明gamma默认情况下函数自动选为维度的倒数
    所以在实验中gamma选择从1到维度的2倍即512。
    步长选为8.使得在能够得到64个数据点。
将数据集随机分成2部分，一部分作为测试集合，另一部分作为训练集。
训练集与测试集完全无交集。
为了防止随机误差。对每一步都测试10遍。最后结果取均值。

实验结果：

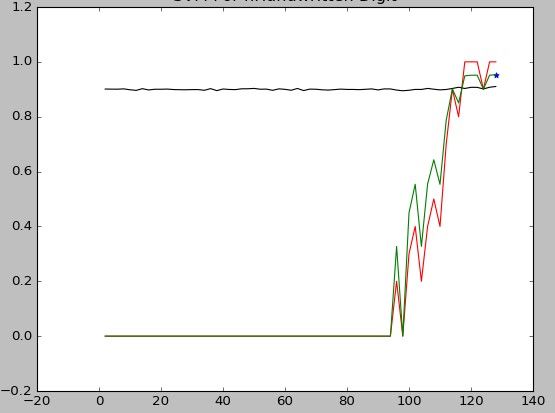
其中，                 
横坐标为sigma值，     
纵坐标为比率，         
红线为召回率，         
黑线为准确率，         
绿线为F值。          
* 为F最大值：（40，0.987483）

结论：

可以看出。在对所给特征不做任何处理的情况下，对于SVM 核函数选用RBF ，参数sigma设为40.可得到极高的F1-Measure。 高达98.7483%。多次测试结果相对稳定。

现在考虑对其进行特征选取:

先对数据进行分析：

获取所有代表5的数据
取均值u = mean(img(tmp,:)); 
输出u：
各个像素点的深浅代表由均值决定。
在中间部分较浅。

对于其他数据：

可以看出，对于类5的数据，其存在大致的轮廓。所以现在考虑使用轮廓特征提取。

轮廓特征提取：

对于256维数据数据。。转成16*16矩阵。对矩阵每一行列，存储其第一个非零字符出现位置。这样对于每一个样本。可以将256维数据转成 64 维数据。

进行SVM分类。

同之前的操作
为了在2倍维度内得到64个点。设置步长为2.

得到结果：

其中，                 
横坐标为sigma值，     
纵坐标为比率，         
红线为召回率，         
黑线为准确率，         
绿线为F值。          
* 为F最大值：（128，0.952976）

结论：

可以看出sigma取点过于靠后。所以猜测在sigma取更大值时.可得到更高的F1-Measure。对于前面召回率持续为0，考虑可能是预测中将所有检测样本全部判错 = =。

重新进行SVM分类:

这次sigma参数选取范围为[0,4096] ,取64个点。4096为维度的平方。
4096这个值的选择是根据RBF核函数公式：

 GaussianRBF:Φ(x,z)=e−(∥x−z∥2σ)
根据上式，sigma取值在1到维度平方都可能有效。
(有些地方写的sigma是2次方。我暂时没有看python中SVM的官方文档里面的说明。不知道他在这里是怎么样设置的。)

其中，                 
横坐标为sigma值，     
纵坐标为比率，         
红线为召回率，         
黑线为准确率，         
绿线为F值。          
* 为F最大值：（1152，0.990615）

结论：

重复多次上述实验。得到F最大值的sigma位置不稳定。但是最大概率在99.05左右。

附录：
代码：

# -*- coding: utf-8 -*-
# !/usr/bin/env python

import numpy
from sklearn import svm
import matplotlib.pyplot as plt


"""
    加载数据
"""
def load_data(path):
    sample_set = numpy.loadtxt(path)
    return sample_set


"""
    提取轮廓特征
"""
def getshape(data):
    len_data = len(data)
    sample = numpy.zeros([len_data, 74])
    for l in range(len_data):
        line = data[l]
        class_die = line[256:]

        tmp_img = line[:256]
        tmp_img = tmp_img.reshape(16, 16)
        for j in range(16):
            # 行第一个
            for k in range(16):
                if tmp_img[j][k] != 0:
                    sample[l][j] = k
                    break
            # 列第一个
            for k in range(16):
                if tmp_img[k][j] != 0:
                    sample[l][j + 16] = k
                    break
            # 行最后一个
            for k in range(16):
                if tmp_img[j][15 - k] != 0:
                    sample[l][j + 32] = k
                    break
            # 列最后一个
            for k in range(16):
                if tmp_img[15 - k][j] != 0:
                    sample[l][j + 48] = k
                    break
            sample[l][64:] = class_die
    return sample


"""
    通过打乱数据。进行数据随机化。
    没有保证2类数据在训练集和测试集相同是因为：
        考虑现实实际情况不存在，
        并且在多次随机统计情况下
        可以确定训练模型参数的优劣
"""
def randomize(data):

    count = len(data) / 2
    numpy.random.shuffle(data)
    set1 = data[0:count, :]
    set2 = data[count:, :]
    return set1, set2


"""
    获取支持向量机，通过sklearn自带函数。
"""
def train_machine(train_feature, train_class, gamma='auto'):
    train = svm.SVC(C=1.0, kernel="rbf", gamma=gamma)
    train.fit(train_feature, train_class)
    return train

"""
统计测试样本的结果:
    计算准确率:
    将实际类型减去预测类型。相同则为0.不同则非0。
    通过计算0的比例。得到准确率

"""
def statistics(real_class,pre_class):
    tmp_list = real_class - pre_class
    tmp_len = len(tmp_list)
    # miss为不正确预测的行数。
    miss = numpy.nonzero(tmp_list)
    match = 1 - 1.0 * len(miss[0]) / tmp_len
    # 召回率。
    re = 0.0
    # 预测结果中类5的预测。
    prelist = numpy.nonzero(pre_class)
    pr = len(prelist[0])
    for tmp in prelist[0]:
        if real_class[tmp] == 1:
            re += 1
    # 除数为零处理
    if pr != 0:
        recall = 1.0 * re / pr
    else:
        recall = 0.0
        # 记录召回率和准确率。
    return recall, match


"""
    建立
"""
def Master(node=64, get_shape=False, max_gamma="auto"):
    # 加载数据
    sample_set = load_data('semeion.data')

    if get_shape:
        sample_set = getshape(sample_set)
        shape = 64
    else:
        shape = 256
    if max_gamma == "auto":
        max_gamma = shape * 2
    else:
        if max_gamma < node:
            max_gamma = node * 2

    """
    计算RBF参数sigma 从[0,max_gamma]范围内对分类器的影响：
    实际上是{step,max_gamma+step],即整体向右偏移了step.
    因为 0不能取啊。= =。用[1,max_gamma+1]的话不方便。
    """
    recall_list = [0.0] * node
    precision_list = [0.0] * node
    f_measure = [0.0] * node
    step = max_gamma / node
    x = [i for i in range(step, max_gamma + step, step)]
    most = [0, 0.0]
    for i in range(step, max_gamma + step, step):
        # 每次使用10次随机的均值作为计算结果。
        # 在输出list中的位置site
        site = i/step -1
        for j in range(10):
            # 训练集和测试集的建立...
            test_set, train_set = randomize(sample_set)
            train_feature = train_set[:, 0:shape]
            train_class = train_set[:, shape + 5]
            test_feature = test_set[:, 0:shape]
            test_class = test_set[:, shape + 5]
            # 建立训练模型。
            gamma = 1.0 / i
            train_model = train_machine(train_feature, train_class, gamma)
            # 预测测试模型
            pre = train_model.predict(test_feature)
            recall, match = statistics(test_class, pre)
            recall_list[site] += recall
            precision_list[site] += match
        print "i: %d " % i
        recall_list[site] /= 10
        precision_list[site] /= 10
        f_measure[site] = 2 * recall_list[site] * precision_list[site] / (recall_list[site] + precision_list[site])
        # 记录 F_measure中最大值。
        most[0] = most[0] if f_measure[site] < most[1] else (site + 1) * step
        most[1] = most[1] if f_measure[site] < most[1] else f_measure[site]
    print "site: %d ;most: %f " % (most[0], most[1])
    plt.figure(1)
    plt.title("SVM For Handwritten Digit")
    plt.plot(x, recall_list,
             label=u'recall',
             color='red')
    plt.plot(x, precision_list,
             label=u'precision',
             color='black')
    plt.plot(x, f_measure,
             label=u'F',
             color='green')
    plt.scatter(most[0], most[1],
                marker='*',
                color='blue')

    plt.show()

if __name__ == '__main__':
    """
    参数输入
    Node:测试点数，默认64
    Get_shape: 使用特征提取，默认无
    Max_gamma: 核函数gamma取值上限，必须高于node点,= =低了就设为 node*2。默认2倍维度。
    """
    Node = 64
    Get_shape = True
    Max_gamma = 4096
    Master(Node, Get_shape, Max_gamma)