《机器学习》学习笔记——Chapter3
1 线性模型
基本形式
1、输入数据 x ⃗ = ( x 1 ; x 2 ; ⋯ ; x d ) \vec x=(x_1; x_2;\cdots;x_d) x=(x1;x2;⋯;xd),有 d d d个属性;
2、通过属性的线性组合,线性模型学得一个可以预测的函数
f ( x ⃗ ) = ω 1 x 1 + ω 2 x 2 + ⋯ + ω d x d + d f(\vec x)=\omega_1 x_1+\omega_2 x_2+\cdots+\omega_d x_d+d f(x)=ω1x1+ω2x2+⋯+ωdxd+d
向量形式
f ( x ⃗ ) = ω ⃗ T x ⃗ + b f(\vec x)=\vec\omega^T\vec x+b f(x)=ωTx+b
3、模型确定的过程在于 ω ⃗ \vec \omega ω和 b b b的学得。
基本思想
1、简单的线性模型通过引入层级结构或高维映射可以得到复杂且功能强大的非线性模型;
2、因为 ω ⃗ \vec \omega ω的各分量是对应属性的系数,直观表达了各属性在预测中的重要程度,所以模型具有很好的可解释性。
接下来的篇幅,将从简单的单变量线性回归开始,进一步介绍多变量线性回归,推广到更一般的广义线性模型——对数几率回归,通过广义线性模型将线性模型应用到分类任务中,由此引出二分类和多分类学习任务,在二分类问题中,学习了一种经典的线性学习方法——LDA线性判别分析,最后是介绍了类别不平衡问题。
2 线性回归
2.1 单变量线性回归
理论概述
1、训练数据集只有一个输入属性
D = { ( x i , y i ) } i = 1 m , x i ∈ R D=\lbrace(x_i, y_i)\rbrace_{i=1}^m,x_i\in R D={(xi,yi)}i=1m,xi∈R
2、目标学得的预测函数
f ( x i ) = ω x i + b f(x_i)=\omega x_i+b f(xi)=ωxi+b
3、通过训练数据集求得 ω \omega ω和 b b b的最佳值,使得
f ( x i ) ≈ y i f(x_i) \approx y_i f(xi)≈yi
公式推导
以预测函数与训练数据的实际输出之间的差值作为衡量标准,此处使用均方误差作为回归任务的性能度量,使预测值与实际输出值之间误差尽可能的小也就是均方误差尽可能的小,这种方法就是最小二乘法。
在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。
所以代价函数就是
J ( ω , b ) = ∑ i = 1 m ( f ( x i ) − y i ) 2 (1) J(\omega,b)=\sum_{i=1}^m(f(x_i)-y_i)^2 \tag{1} J(ω,b)=i=1∑m(f(xi)−yi)2(1)
上(1)式代入 f ( x i ) f(x_i) f(xi)得
J ( ω , b ) = ∑ i = 1 m ( y i − ω x i − b ) 2 (2) J(\omega,b)=\sum_{i=1}^m(y_i-\omega x_i-b)^2 \tag{2} J(ω,b)=i=1∑m(yi−ωxi−b)2(2)
求解 ω \omega ω和 b b b使 J ( ω , b ) J(\omega,b) J(ω,b)最小化的过程,称为线性回归模型的最小二乘“参数估计”。
求解使得(2)式最小的参数,可将(2)式分别对两个参数求偏导数,这里涉及到凸函数和多元函数求偏导数的概念
\begin{align}
\frac {\partial J_{(\omega,b)}}{\partial \omega}
& = \frac {\partial \sum_{i=1}^m(y_i-\omega x_i-b)^2}{\partial \omega},\tag{3} \
& = 2\cdot \sum_{i=1}^m(y_i-\omega x_i-b)(-x_i)\tag{4}\
& = 2 \cdot \sum_{i=1}^m(\omega x_i^2-(y_i-b)x_i)\tag{5}\
& = 2(\omega \sum_{i=1}^m x_i2-\sum_{i=1}m(y_i-b)x_i),\tag{6}
\end{align}
\begin{align}
\frac {\partial J_{(\omega,b)}}{\partial b}
& = \frac {\partial \sum_{i=1}^m(y_i-\omega x_i-b)^2}{\partial \omega} \tag{7} \
& = 2\cdot \sum_{i=1}^m(y_i-\omega x_i-b)(-1)\tag{8}\
& = 2 \cdot \sum_{i=1}^m(b-(y_i-\omega x_i)) \tag{9}\
& = 2(mb-\sum_{i=1}^m(y_i-\omega x_i)),\tag{10}
\end{align}
在从(3) $\rightarrow $ (4)和(7) $\rightarrow $ (8)的推导过程中用到了复合函数求偏导,这属于大学高等数学的范围,之后就是简单的合并。
然后令(6),(10)分别为零可以求得参数最优解的闭式解
ω ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i = 0 , (11) \omega \sum_{i=1}^m x_i^2-\sum_{i=1}^m(y_i-b)x_i=0,\tag{11} ωi=1∑mxi2−i=1∑m(yi−b)xi=0,(11)
m b − ∑ i = 1 m ( y i − ω x i ) = 0 , (12) mb-\sum_{i=1}^m(y_i-\omega x_i)=0,\tag{12} mb−i=1∑m(yi−ωxi)=0,(12)
由(12)可得
b = 1 m ∑ i = 1 m ( y i − ω x i ) , (13) b=\frac{1}{m}\sum_{i=1}^m(y_i-\omega x_i),\tag{13} b=m1i=1∑m(yi−ωxi),(13)
将(13)代入(11)得
ω ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − 1 m ∑ i = 1 m ( y i − ω x i ) ) x i = 0 , (14) \omega \sum_{i=1}^m x_i^2-\sum_{i=1}^m(y_i-\frac{1}{m}\sum_{i=1}^m(y_i-\omega x_i))x_i=0,\tag{14} ωi=1∑mxi2−i=1∑m(yi−m1i=1∑m(yi−ωxi))xi=0,(14)
ω ∑ i = 1 m x i 2 = ∑ i = 1 m ( x i y i − 1 m x i ∑ i = 1 m y i + ω ⋅ 1 m x i ∑ i = 1 m x i ) , (15) \omega \sum_{i=1}^m x_i^2=\sum_{i=1}^m(x_iy_i-\frac{1}{m}x_i\sum_{i=1}^my_i+\omega \cdot \frac{1}{m}x_i\sum_{i=1}^mx_i),\tag{15} ωi=1∑mxi2=i=1∑m(xiyi−m1xii=1∑myi+ω⋅m1xii=1∑mxi),(15)
移项
\begin{align}
\omega(\sum_{i=1}mx_i2-\frac{1}{m}(\sum_{i=1}mx_i)2)
&=\sum_{i=1}m(x_iy_i-\frac{1}{m}x_i\sum_{i=1}my_i),\tag{16}\
&=\sum_{i=1}mx_iy_i-\sum_{i=1}m\overline{x}y_i,\tag{17}\
&=\sum_{i=1}^my_i(x_i-\overline{x}),\tag{18}
\end{align}
可得
ω = ∑ i = 1 m y i ( x i − x ‾ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 , (19) \omega=\frac{\sum_{i=1}^my_i(x_i-\overline{x})}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2},\tag{19} ω=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−x),(19)
2.2 多变量线性回归
理论概述
1、训练数据集D有d个输入属性,一共有m个样本数据,D可以表示为矩阵
X = ( x 11 x 12 ⋯ x 1 d 1 x 21 x 22 ⋯ x 2 d 1 ⋯ x m 1 x m 2 ⋯ x m d 1 ) X=\begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1\\ \cdots \\ x_{m1} & x_{m2} & \cdots & x_{md} & 1 \end{pmatrix} X=⎝⎜⎜⎛x11x21⋯xm1x12x22xm2⋯⋯⋯x1dx2dxmd111⎠⎟⎟⎞
每行对应一个样本,该行前d个元素对应于样本的d个元素值,最后一个元素恒为1。
所以属性可以用向量表示
x ⃗ i = ( x i 1 ; x i 2 ; ⋯ ; x i d ) \vec x_i=(x_{i1};x_{i2};\cdots;x_{id}) xi=(xi1;xi2;⋯;xid)
2、目标学得的预测函数
f ( x ⃗ i ) = ω ⃗ T x ⃗ i + b f(\vec x_i)=\vec \omega^T \vec x_i+b f(xi)=ωTxi+b
系数向量 ω ⃗ = ( ω 1 ; ω 2 ; ⋯ ; ω d ) \vec \omega=(\omega1;\omega2;\cdots;\omega d) ω=(ω1;ω2;⋯;ωd)
3、通过训练数据集求得 ω \omega ω和 b b b的最佳值,使得
f ( x ⃗ i ) ≈ y i f(\vec x_i) \approx y_i f(xi)≈yi
也叫做“多元线性回归”
公式推导
此处对 ω \omega ω和 b b b的确定也可以使用最小二乘法,为了公式推导的方便,此处做了一些整理, ω ⃗ ^ = ( ω ; b ) \hat{\vec \omega}=(\omega;b) ω^=(ω;b),数据集中样本的标记用向量表示为 y ⃗ = ( y 1 ; y 2 ; ⋯ ; y m ) \vec y=(y_1;y_2;\cdots;y_m) y=(y1;y2;⋯;ym),类比(2)可以得到代价函数
J ω ⃗ ^ = ( y ⃗ − X ω ) 2 , (20) J_{\hat {\vec \omega}}=(\vec y-X\omega)^2,\tag{20} Jω^=(y−Xω)2,(20)
根据矩阵乘法可以表示为矩阵的转置乘以矩阵
J ω ⃗ ^ = ( y ⃗ − X ω ) T ( y ⃗ − X ω ) , (21) J_{\hat {\vec \omega}}=(\vec y- X\omega)^T(\vec y- X\omega),\tag{21} Jω^=(y−Xω)T(y−Xω),(21)
对 ω ⃗ ^ \hat{\vec \omega} ω^求导可得
这里的矩阵求导引用同学推荐的资源一份来自维基百科-矩阵求导,另一份则是一份说明性质的微博
\begin{align}
\frac {\partial J_{\hat{\vec \omega}}}{\partial \hat{\vec \omega}}
& = \frac {\partial (\vec y- X_i)^T(\vec y- X_i)}{\partial \hat{\vec \omega}}, \tag{22} \
& = \frac {\partial (\vec y^T\vec y-\hat{\vec \omega}^T\vec X^T \vec y-\vec y^T \vec X\hat{\vec \omega} + \hat{\vec \omega}^T \vec X^T \vec X \hat{\vec \omega})}{\partial \hat{\vec \omega}} ,\tag{23}\
& = 0 - \vec X^T \vec y-(\vec y^T \vec X)^T+2\vec X^T \vec X \vec \omega ,\tag{24}\
& = 2 X^T (X \hat{\vec \omega}-\vec y),\tag{25}
\end{align}
上边的推导过程难点在于从(23) → \rightarrow →(24)的过程,首先判断为分母为列向量,则为分母布局,(23)第一项求导的分子为标量,则求导结果为零,第二项分子为分母列向量的转置和一个(d+1)$\times 1 的 列 向 量 的 点 乘 , 第 三 项 分 子 为 一 个 1 1的列向量的点乘,第三项分子为一个1 1的列向量的点乘,第三项分子为一个1\times$(d+1)的行向量和分母列向量的点乘,对照
维基百科-矩阵求导
表格中的第10行可得对应求导结果,第四项则是对应第13行的求导规则进行求导,矩阵的转置乘以矩阵本身是一个对称矩阵。**
此外,在这里求导时,有一个比较简单的方法,参考西瓜书402面的链式求导法则和式(A.32)的举例,可以快速准确的得到答案
令(25)为零可得 ω ⃗ ^ \hat{\vec \omega} ω^最优解的闭式解,此处因为涉及到矩阵逆的计算,所以需要分类讨论:
当 X T X X^TX XTX为满秩矩阵或正定矩阵,矩阵的逆存在,所以由(25)为零可得
X T X ω ⃗ ^ = X T y ⃗ , (26) X^TX \hat{\vec \omega}=X^T \vec y , \tag{26} XTXω^=XTy,(26)
等式两边同乘逆矩阵 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1可得
ω ⃗ ^ ∗ = ( X T X ) − 1 X T y ⃗ , (27) \hat{\vec \omega}^*=(X^TX)^{-1}X^T \vec y, \tag{27} ω^∗=(XTX)−1XTy,(27)
令 x ⃗ ^ = ( x ⃗ ; 1 ) \hat{\vec x}=(\vec x;1) x^=(x;1),则可得多变量线性回归模型
f ( x ⃗ i ^ ) = x ⃗ i ^ T ( X T X ) − 1 X T y ⃗ , (28) f(\hat{\vec x_i})=\hat{\vec x_i}^T(X^TX)^{-1}X^T\vec y,\tag{28} f(xi^)=xi^T(XTX)−1XTy,(28)
但是很多情况下,数据集的变量数目远远大于样本数,即 X X X的列数多于行数,这种情况下相当于(25)为零所对应的线性方程组存在多组解,都能使均方误差最小化,最后选择哪一组解作为输出将由学习算法的归纳偏好决定,一般引入正则化来解决这个问题
3 广义线性模型
理论概述
此部分是对上边已经得到的线性模型
y = ω ⃗ T x ⃗ + b y=\vec\omega^T\vec x+b y=ωTx+b
进行变化,我们的目标是使此模型的预测值尽可能地逼近真实的输出值,当样本对应的输出值是在指数尺度上变化,就可以将输出值的对数作为线性模型逼近的目标,上式也就变化为如下形式
l n y ⃗ = ω ⃗ T x ⃗ + b , (29) ln\ \vec y=\vec\omega^T\vec x+b,\tag{29} ln y=ωTx+b,(29)
上式就是**“对数线性回归”(log-linear regression),其实质是如下式子
y = e ω ⃗ T x ⃗ + b , (30) y=e^{\vec \omega^T\vec x+b},\tag{30} y=eωTx+b,(30)
对于(29)来说,在形式上仍是线性回归,但是经过(30)的变换就可以发现这是一个从输入空间到输出空间的非线性函数映射**,在这里对数函数起的作用就是将线性回归模型的预测值与真实输出值联系起来。通过下图可以清楚地看到这种联系。
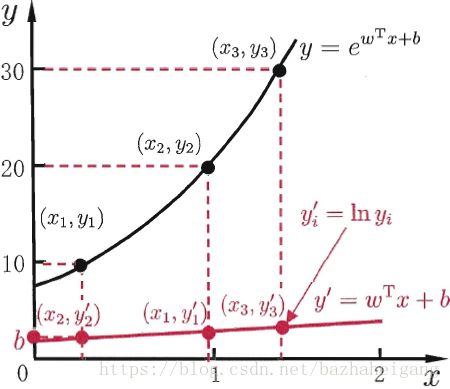
图 1 对 数 线 性 回 归 示 意 图 图1\ 对数线性回归示意图 图1 对数线性回归示意图
由此推至更一般的形式,存在单调可微函数 g ( ⋅ ) g(\cdot) g(⋅),可以更一般的表达上边对数函数所起的这种联系
y = g − 1 ( ω ⃗ T x ⃗ + b ) , (31) y=g^{-1}(\vec \omega^T \vec x+b),\tag{31} y=g−1(ωTx+b),(31)
至此我们得到(31)就是**“广义线性模型(generalized linear model)”**,函数 g ( ⋅ ) g(\cdot) g(⋅)为“联系函数(link function)”。当 g ( ⋅ ) = l n ( ⋅ ) g(\cdot)=ln(\cdot) g(⋅)=ln(⋅)时,广义线性模型就是我们前边讨论的对数线性回归,对此类模型的参数估计通常使用加权最小二乘法或极大似然法。
4 对数几率回归
理论概述
至此,我们已经学习了如何使用线性模型进行回归学习,考虑到如何应用的实际的分类任务,我们的做法就是利用线性回归模型,根据实际的分类任务,选择一个合适的单调可微函数将分类任务的真实输出值与线性回归模型的预测值联系起来。
对于输出值为 0 , 1 {0,1} 0,1的二分类任务,我们需要找到一类函数,将线性回归模型的实值预测值 z = ω ⃗ T x ⃗ + b z=\vec \omega^T \vec x + b z=ωTx+b转换为 0 / 1 {0/1} 0/1值,最想的首选是**“单位阶跃函数(unit-step function)”**
y = { 0 , if n < 0 0.5 , if z = 0 1 , if z >0 (32) y = \begin{cases} 0, & \text{if $n$ < 0} \\ 0.5, & \text{if $z$ = 0} \\ 1, & \text{if $z$ >0} \end{cases} \tag{32} y=⎩⎪⎨⎪⎧0,0.5,1,if n < 0if z = 0if z >0(32)
预测值 z z z大于零则判断为正例,小于零则为反例,当为临界值零则任意判别;但是从图中可以看出单位阶跃函数在零处不连续,不满足广义线性模型中可微的条件,我们只能寻找相似函数来代替,这里就引出了我们要讨论的对数几率函数
y = 1 1 + e − z , (33) y=\frac{1}{1+e^{-z}},\tag{33} y=1+e−z1,(33)
这是Sigmoid函数的最重要的代表,这里扩展一下,还可以使用双曲正切函数tanH来代替,因为输出区间为 ( − 1 , 1 ) (-1,1) (−1,1),且整个函数以0为中心,在分类问题中往往会有更好的表现,下图直观的表现了对数几率函数可以很好地将 z z z值转化为接近 0 / 1 0/1 0/1的 y y y值,近似于标准的单位阶跃函数
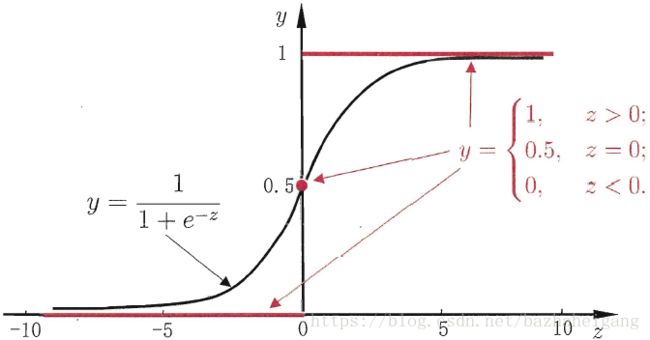
图 2 单 位 阶 跃 函 数 和 对 数 几 率 函 数 图2 单位阶跃函数和对数几率函数 图2单位阶跃函数和对数几率函数
将(33)作为联系函数代入广义线性模型即可得到
y = 1 1 + e − ( ω ⃗ T x ⃗ + b ) , (34) y=\frac{1}{1+e^{-(\vec \omega^T \vec x+b)}},\tag{34} y=1+e−(ωTx+b)1,(34)
变形为
l n y 1 − y = ω ⃗ T x ⃗ + b , (35) ln{\frac{y}{1-y}}=\vec \omega^T\vec x+b,\tag{35} ln1−yy=ωTx+b,(35)
接下来说明对数几率的来源,可以将上式中 y y y看作样本 x x x正例的可能性, 1 − y 1-y 1−y也就是反例可能性,将两者比值称为**“几率(odds)”,表现了 x x x作为正例的相对可能性。则对几率取对数就得到“对数几率(log odds also logit)”。至此,我们再回过头去看(34),就明白相比于之前讨论的线性回归模型,对数几率回归其实是将模型的预测输出值逼近真实输出值的对数几率**,同时也要注意,虽然也叫“回归”,但实际上是一种应用于分类任务的学习方法,具有如下优点:
(1)可直接建模,无需假设数据分布,避免假设分布不准确的问题;
(2)不仅可以预测类别,还可以完成近似概率预测;
(3)对数几率函数还是任意阶可导的凸函数,可用许多数值优化算法直接求取最优解。
###公式推导###
与在线性回归中的推导一样,我们得到模型的表达式,就需要确定函数中参数 ω ⃗ \vec \omega ω和 b b b,将(34)中的 y y y看作类后验概率估计,这里讨论的类后验概率可以点击超链接进行了解,我这里以自己的理解来简单介绍一下,在这里就是,代表某件事的 x x x输入了模型,也就是这件事发生了,这个后验概率就代表这个输入 x x x也就是这件发生的事属于某一类别的概率,借此,我们就可以对 x x x这类事进行归类,后验概率越大,此事属于这个类别的概率也就越大。
(35)可以重写成
l n p ( y = 1 ∣ x ⃗ ) p ( y = 0 ∣ x ⃗ ) = ω ⃗ T + b , (36) ln\frac{p(y=1|\vec x)}{p(y=0|\vec x)}=\vec \omega^T+b,\tag{36} lnp(y=0∣x)p(y=1∣x)=ωT+b,(36)
根据概率知识 p ( y = 1 ∣ x ⃗ ) + p ( y = 0 ∣ x ⃗ ) = 1 p(y=1|\vec x)+p(y=0|\vec x)=1 p(y=1∣x)+p(y=0∣x)=1可得后验概率估计表达式
p ( y = 1 ∣ x ⃗ ) = e ω ⃗ T + b 1 + e ω ⃗ T + b , (37) p(y=1|\vec x)=\frac {e^{\vec \omega^T+b}}{1+e^{\vec \omega^T+b}},\tag{37} p(y=1∣x)=1+eωT+beωT+b,(37)
p ( y = 0 ∣ x ⃗ ) = 1 1 + e ω ⃗ T + b , (38) p(y=0|\vec x)=\frac {1}{1+e^{\vec \omega^T+b}},\tag{38} p(y=0∣x)=1+eωT+b1,(38)
接下来就是使用极大似然法(ML)来对参数进行估计,在这个超链接中是一篇对极大似然估计的详解,大家可以作为参考。
在对数几率回归模型中,我们可以得到对于数据集 ( x ⃗ i , y i ) i = 1 m {(\vec x_i,y_i)}_{i=1}^m (xi,yi)i=1m的对数似然函数
l ( ω ⃗ , b ) = ∑ i = 1 m l n p ( y i ∣ x ⃗ i ; ω ⃗ , b ) , (39) l(\vec \omega, b)=\sum_{i=1}^m ln \ p(y_i|\vec x_i;\vec \omega,b),\tag{39} l(ω,b)=i=1∑mln p(yi∣xi;ω,b),(39)
在这里我谈谈我对这部分的理解,我们之所以使用极大似然法来估计参数,其实是利用这个似然函数来作为一个对模型的评价机制,我们仔细分析(39)可以看到,除了参数 ω ⃗ , b \vec \omega,b ω,b未知,还有一个未知变量就是类后验概率估计p( ⋅ \cdot ⋅),这是因为对于确定的数据集,如果使用不同的模型去估计每个样本属于其真实输出值的概率是不一样,当模型的参数改变的时候,这个概率也就是后验概率会发生变化,我们评价标准就是这个概率越大越好,从而找到使这个概率最大时候的参数,从而确定最优的模型,所以针对一个数据集来说,我们就可以得到(39)所示的对数似然函数,这中间省略了一些基本的变化,大家可以参看我上边引用的极大似然法那个博客
按照书本书里的处理方法,我也在这里对式子进行一些简化方便后边的讨论
令 β ⃗ = ( ω ⃗ ; b ) , x ⃗ ^ = ( x ⃗ ; 1 ) \vec \beta=(\vec \omega;b),\hat{\vec x}=(\vec x;1) β=(ω;b),x^=(x;1),
则 ω ⃗ T x ⃗ + b = β ⃗ T x ⃗ ^ \vec \omega^T\vec x+b=\vec \beta^T\hat{\vec x} ωTx+b=βTx^;
再令
p 1 ( x ⃗ ^ ; β ⃗ ) = p ( y = 1 ∣ x ⃗ ; β ⃗ ) p_1(\hat {\vec x};\vec \beta)=p(y=1|\vec x;\vec \beta) p1(x^;β)=p(y=1∣x;β),
p 0 ( x ⃗ ^ ; β ⃗ ) = p ( y = 0 ∣ x ⃗ ; β ⃗ ) = 1 − p 1 ( x ⃗ ^ ; β ⃗ ) p_0(\hat {\vec x};\vec \beta)=p(y=0|\vec x;\vec \beta)=1-p_1(\hat {\vec x};\vec \beta) p0(x^;β)=p(y=0∣x;β)=1−p1(x^;β)
则(39)中的似然项可变为
p ( y i ∣ x ⃗ i ; ω ⃗ , b ) = y i p 1 ( x ⃗ ^ ; β ⃗ ) + ( 1 − y i ) p 0 ( x ⃗ ^ ; β ⃗ ) , (40) p(y_i|\vec x_i;\vec \omega,b)=y_ip_1(\hat {\vec x};\vec \beta)+(1-y_i)p_0(\hat {\vec x};\vec \beta),\tag{40} p(yi∣xi;ω,b)=yip1(x^;β)+(1−yi)p0(x^;β),(40)
上式其实一个条件函数的变形,若输出值为1则上式右边第一项保留,第二项为零;同理,当第一项为零,第二项保留就是输出值为0的情况。将(40)代入(39),再用(37)(38)代替(40) p 1 ( ⋅ ) , p 0 ( ⋅ ) p_1(\cdot),p_0(\cdot) p1(⋅),p0(⋅)两项,推导过程如下
l ( β ⃗ ) = ∑ i = 1 m l n ( y i e β ⃗ T x ⃗ ^ 1 + e β ⃗ T x ⃗ ^ + ( 1 − y i ) 1 1 + e β ⃗ T x ⃗ ^ ) , (41) l(\vec \beta)=\sum_{i=1}^mln\ (y_i\frac{e^{\vec \beta^T \hat{\vec x}}}{1+e^{\vec \beta^T \hat{\vec x}} }+(1-y_i)\frac {1}{1+e^{\vec \beta^T \hat{\vec x}}}),\tag{41} l(β)=i=1∑mln (yi1+eβTx^eβTx^+(1−yi)1+eβTx^1),(41)
整理后可得
l ( β ⃗ ) = ∑ i = 1 m ( l n ( y i e β ⃗ T x ⃗ ^ + ( 1 − y i ) ) − l n ( 1 + e β ⃗ T x ⃗ ^ ) ) , (42) l(\vec \beta)=\sum_{i=1}^m(ln\ (y_i e^{\vec \beta^T \hat{\vec x}}+(1-y_i))-ln(1+e^{\vec \beta^T \hat{\vec x}})),\tag{42} l(β)=i=1∑m(ln (yieβTx^+(1−yi))−ln(1+eβTx^)),(42)
对上式的整理可以使用条件函数简化的思想
当 y i = 0 y_i=0 yi=0可以得到
l ( β ⃗ ) = ∑ i = 1 m ( − l n ( 1 + e β ⃗ T x ⃗ ^ ) ) , (43) l(\vec \beta)=\sum_{i=1}^m(-ln(1+e^{\vec \beta^T \hat{\vec x}})),\tag{43} l(β)=i=1∑m(−ln(1+eβTx^)),(43)
当 y i = 1 y_i=1 yi=1可以得到
l ( β ⃗ ) = ∑ i = 1 m ( β ⃗ T x ⃗ i ^ − l n ( 1 + e β ⃗ T x ⃗ i ^ ) ) , (44) l(\vec \beta)=\sum_{i=1}^m( \vec \beta^T \hat{\vec x_i}-ln(1+e^{\vec \beta^T \hat{\vec x_i}})),\tag{44} l(β)=i=1∑m(βTxi^−ln(1+eβTxi^)),(44)
由上述两种情况就可以得到下面的式子,这个过程是利用 y i y_i yi要么是1要么就是0这一特性,就将(42)简化成(45)的形式
l ( β ⃗ ) = ∑ i = 1 m ( y i β ⃗ T x ⃗ i ^ − l n ( 1 + e β ⃗ T x ⃗ i ^ ) ) , (45) l(\vec \beta)=\sum_{i=1}^m(y_i \vec \beta^T \hat{\vec x_i}-ln(1+e^{\vec \beta^T \hat{\vec x_i}})),\tag{45} l(β)=i=1∑m(yiβTxi^−ln(1+eβTxi^)),(45)
细心会发现我推导出的式子和书上的(3.27)正好相反,这是因为书上的式子是一个关于 β ⃗ \vec \beta β的高阶可导连续凸函数,这样根据凸优化理论,可以使用一些经典的数值优化算法求得最优解,只不过在我们这里是最大化(45),在书中是最大化下式(46),具体的求解算法如梯度下降法,牛顿法及求解过程在这里不再赘述,将另开博详述,不过在稍后的代码中将会有所体现
l ( β ⃗ ) = ∑ i = 1 m ( − y i β ⃗ T x ⃗ i ^ + l n ( 1 + e β ⃗ T x ⃗ i ^ ) ) , (46) l(\vec \beta)=\sum_{i=1}^m(-y_i \vec \beta^T \hat{\vec x_i}+ln(1+e^{\vec \beta^T \hat{\vec x_i}})),\tag{46} l(β)=i=1∑m(−yiβTxi^+ln(1+eβTxi^)),(46)
至此,本书第三章的前三小节笔记结束,下一篇将剩余部分的总结,可能有的朋友会觉得全文过长赘述,我的想法能将我在学习过程中遇到的问题一一记录下来,并尽可能给出解答,作为我日后复习的一份参考资料。谢谢诸位的阅读。
以下承接前文**《机器学习》学习笔记——Chapter3(3.1-3.3),主要是关于对数几率回归(logistic regression)模型在多分类任务上的推广,解决这类标注也就是分类为两个以上的任务,使用的模型是Softmax回归**。
本文参考ufldl教程中此部分的讲解,大概说一说我本人的一些理解,日后再行补充。
简介
朴素贝叶斯算法:
输入:
数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , x i ∈ R n , y i ∈ { 0 , 1 } ; D = \lbrace(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\rbrace,x_i \in R^n, y_i \in \lbrace0,1\rbrace; D={(x1,y1),(x2,y2),...,(xm,ym)},xi∈Rn,yi∈{0,1};
输出过程
1、假设每个属性独立地对分类结果发生影响;
2、重写贝叶斯公式:
P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) = P ( c ) P ( x ) ∏ i = 1 d P ( x i ∣ c ) P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod_{i=1}^d P(x_i|c) P(c∣x)=P(x)P(c)P(x∣c)=P(x)P(c)∏i=1dP(xi∣c)
3、基于贝叶斯决策论的朴素贝叶斯分类器表达式:
h n b ( x ) = a r g m a x P ( c ) ∏ i = 1 d P ( x i ∣ c ) , c ∈ y h_{nb}(x)=arg \ max P(c) \prod _{i=1}^d P(x_i|c),c \in y hnb(x)=arg maxP(c)∏i=1dP(xi∣c),c∈y
4、基于训练集 D D D估计 P ( c ) P(c) P(c),并为每个属性估计条件概率 P ( x i ∣ c ) P(x_i|c) P(xi∣c),计算同一 x x x在 c = 1 c=1 c=1的 h n b 1 h_{nb1} hnb1和 c = 0 c=0 c=0的 h n b 0 h_{nb0} hnb0
输出
比较 h n b 0 h_{nb0} hnb0和 h n b 1 h_{nb1} hnb1的大小, h n b 0 > h n b 1 h_{nb0}>h_{nb1} hnb0>hnb1则 y = 0 y=0 y=0, h n b 0 < h n b 1 h_{nb0}
SVC算法:
输入:
数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , x i ∈ R n , y i ∈ { 0 , 1 } ; D = \lbrace(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\rbrace,x_i \in R^n, y_i \in \lbrace0,1\rbrace; D={(x1,y1),(x2,y2),...,(xm,ym)},xi∈Rn,yi∈{0,1};
输出过程:
1、得到目标函数
2、转化为不等式约束下的二次型函数优化问题
3、使用拉格朗日函数和KKT条件转化为对偶问题的求解
4、使用SMO算法进行求解
输出
分类器结果