机器学习笔记之——支持向量机（一）

支持向量机（一）

---

1. 主要思想

对于一个二分类问题，其样本分布如下所示，其中 $+,-$ 分别代表正负样本，红色和绿色代表两个线性分类器，这两个分类器哪个更好呢？

虽然这两个分类器都能把两类样本完全分开，训练误差为 0，但是红色的分类器更好，因为其泛化能力更强，即对新样本的判断能力更好。假设我们有两个新样本（如下图紫色样本所示）：

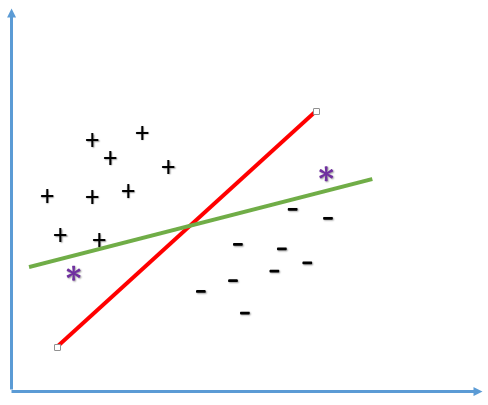
左下角的紫色样本与正样本簇靠在一起，显然其应该属于正样本，同理，右上角的紫色样本理当属于负样本。但是，如果按照绿色分类器的结果，则会把这两个新样本分错。原因是因为其分类边界与样本距离太近了。因此，如果想让分类器的泛化性能较好，就应该让其和红色分类器一样，与样本间的间隔越大越好，这就是支持向量机(Support Vector Machine) 的主要思想。

2. 公式表示

一个线性分类边界可以用方程 ${\mathbf{w}}^T\mathbf{x}+b=0$ 表示，我们假设分类间隔区域与样本接触的两条直线分别是 ${\mathbf{w}}^T\mathbf{x}+b=+1$ 和 ${\mathbf{w}}^T\mathbf{x}+b=-1$，如下图所示：

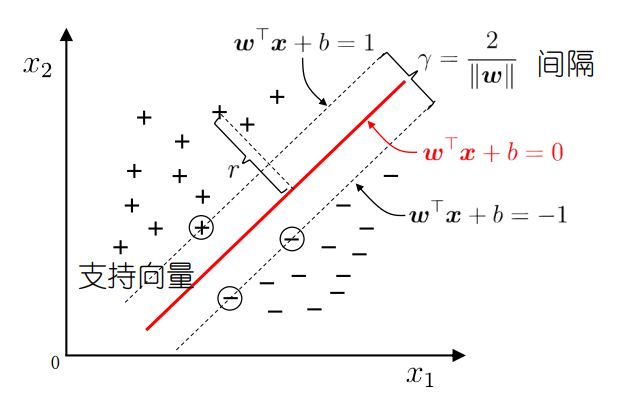
我们希望：

• 当样本在分类间隔带的上方时，即 ${\mathbf{w}}^T\mathbf{x}+b>+1$ 时，把其预测为正类(+1)
• 当样本在分类间隔带的下方时，即 ${\mathbf{w}}^T\mathbf{x}+b<-1$ 时，把其预测为负类(-1)

我们可以把这两个条件统一成一个式子，$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$，其中 ${\mathbf{x}}_i$ 和 $y_i$ 分别表示第 $i$ 个样本的特征和标签，$y_i\in \{+1,-1\}$。计算分类间隔的长度，得到：
$$\gamma =\frac{2}{\Vert \mathbf{w}{\Vert }_2}$$ 那么我们便可以得到 SVM 要求解的目标函数：
$$\underset{\mathbf{w},b}{\max }\frac{2}{\Vert \mathbf{w}{\Vert }_2}$$ $$s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2\dots ,m$$ 这个公式的意义是：在不分错训练样本的约束下（即 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$），使得分类间隔最大化。
显然，上述目标函数可以等价变换成：
$$\underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2\text{\hspace{1em}(1)}$$ $$s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2\dots ,m$$

3. 公式求解

3.1 拉格朗日函数

对每个约束条件乘以拉格朗日乘子 ${\alpha }_i\ge 0$ ，加到目标函数后面，得到拉格朗日函数：
$$L(\mathbf{w},b,\mathbf{\alpha })=\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2+\sum _{i=1}^m{\alpha }_i(1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b))$$ 现在分析一下拉格朗日函数的最大值与原函数的关系：

• 当原来的约束满足时，即对于所有的样本 $i$，都有 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$ 成立，那么 $1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$，此时要想使得 L 函数取得最大值，只需要令所有的 ${\alpha }_i=0$ 即可，此时 $L=\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2$，与原目标函数一致。
• 当原来的约束不满足时，即至少有一个样本 $i$，使得 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)<1$ ，那么对应的 $1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)>0$，此时要想使得 L 函数取得最大值，只需要对应的 ${\alpha }_i=+\infty$ 即可，此时 $L=+\infty$

从以上分析，我们得到：
$$\underset{\mathbf{\alpha }}{\max }L(\mathbf{w},b,\mathbf{\alpha })=\{\begin{array}{ll}\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2,& 若约束满足\\ +\infty ,& 若约束不满足\end{array}$$ 因此优化带约束的原目标函数（1）等价于优化不带约束的下列函数：
$$\underset{\mathbf{w},b}{\min }\underset{\mathbf{\alpha }}{\max }L(\mathbf{w},b,\mathbf{\alpha })\text{\hspace{1em}(2)}$$ 若约束得不到满足的话，上述式子的结果为 $+\infty$，由于外层是求最小值，所以显然 $+\infty$ 不是 $\min$ 想要的结果，因此如果存在参数满足约束的话，上述函数会尽可能往约束满足的方向求解。

3.2 拉格朗日对偶问题

虽然我们把问题转化成了公式（2），但是这个很难求解。此时我们考虑其对偶问题，只要把 $\max$ 和 $\min$ 的次序交换一下，就得到了原问题的对偶问题：
$$\underset{\mathbf{\alpha }}{\max }\underset{\mathbf{w},b}{\min }L(\mathbf{w},b,\mathbf{\alpha })\text{\hspace{1em}(3)}$$ 这个问题比较容易求解，首先求内层最小化问题：
$$\underset{\mathbf{w},b}{\min }L(\mathbf{w},b,\mathbf{\alpha })\text{\hspace{1em}(4)}$$ 只要对参数求导，令其为 0 即可，得到：
$$\mathbf{w}=\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i\text{\hspace{1em}(5)}$$ $$\sum _{i=1}^m{\alpha }_i{y}_i=0\text{\hspace{1em}(6)}$$ 把公式（5）代入公式（4），可得：
$$\begin{array}{rl}\underset{\mathbf{w},b}{\min }L(\mathbf{w},b,\mathbf{\alpha })& =\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2+\sum _{i=1}^m{\alpha }_i(1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b))\\ & =\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\\ & =\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+\sum _{i=1}^m{\alpha }_i-{\mathbf{w}}^T\mathbf{w}-0(利用公式(5),(6))\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\end{array}$$ 所以对偶问题转化为：
$$\underset{\mathbf{\alpha }}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\text{\hspace{1em}(7)}$$ $$\begin{array}{rl}s.t.& \sum _{i=1}^m{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0,i=1,2,\dots ,m\end{array}$$

3.3 KKT 条件

前面我们一直在尝试求对偶问题的解，但是对偶问题与原问题真的完全等价吗？求出了对偶问题的最优值就能得到原问题的最优值吗？答案是不一定。但是对偶问题与原问题之间确实存在一定的联系。令 $p^{\ast }$ 为原问题的最优值，$d^{\ast }$ 是对偶问题的最优值：

• 在任何情况下，都有 $d^{\ast }\le p^{\ast }$ 成立，这个性质称为弱对偶性。
• 当原问题是凸问题，且 Slater 条件满足时，有 $d^{\ast }=p^{\ast }$，这个被称为强对偶性。

原问题公式（1）的目标函数和约束条件都是凸函数，因此原问题是凸问题。另外，由于约束函数是仿射函数，因此只要存在参数满足公式（1）的约束（即只要样本是线性可分的），那么 Slater 条件就满足。由此我们可以看出，对于这个问题，强对偶性是成立的。所以，我们只要求出对偶问题的最优值，就可断定其一定也是原问题的最优值。

不过，我们提到的是原问题和对偶问题的最优值相等，其实它们的最优解之间也存在一定的联系。令 $\mathbf{w},b$ 是原问题的最优解，$\mathbf{\alpha }$ 是对偶问题的最优解，$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b$, 那么对于 $i=1,2\dots ,m$， 一定有下列关系满足：
$$\{\begin{array}{l}{y}_{i}f({\mathbf{x}}_i)\ge 1\\ {\alpha }_i\ge 0\\ {\alpha }_i(y_{i}f({\mathbf{x}}_i)-1)=0\\ \frac{\partial L}{\partial \mathbf{w}}=0\\ \frac{\partial L}{\partial b}=0\end{array}$$ 上述条件被称作 KKT 条件。当原问题是凸问题且强对偶性成立时，KKT 条件是最优解的充分必要条件。

从公式（5）可以看出，参数 $\mathbf{w}$ 是样本 ${\mathbf{x}}_i$ 的线性组合，权重为 ${\alpha }_i$（因为 $y_i\in \{+1,-1\}$，只决定符号，不影响大小）。 现在我们重点关注第三个条件，被称为互补松弛性条件， ${\alpha }_i(y_{i}f({\mathbf{x}}_i)-1)=0$，具体分析如下：

• 若 $y_{i}f({\mathbf{x}}_i)-1>0$，那么必有 ${\alpha }_i=0$，也就是说该样本不会在公式（5）的求和出现，不会对分类边界产生影响；
• 若 ${\alpha }_i>0$，那么必有 $y_{i}f({\mathbf{x}}_i)-1=0$，也就是说该样本在分类最大间隔的边界上，会在公式（5）中的求和中出现，因此会影响到分类边界。

所以可以看出，分类边界的参数 $\mathbf{w}$ 只与少数的那些在边界上（即 ${\alpha }_i>0$）的样本有关，这些样本被称为支持向量，这就是支持向量机的名字由来。

3.4 求解

对公式（7）进行求解，解得一组 ${\alpha }_i$。常用的算法是 SMO(Sequential Minimal Optimization) 算法，SMO 算法不断执行下列两个步骤直到收敛：

• 选取一对需要更新的 ${\alpha }_i,{\alpha }_j$
• 固定除了这两个变量之外的参数，更新 ${\alpha }_i,{\alpha }_j$

求出 $\mathbf{\alpha }$ 之后，代入公式（5）即可求出 $\mathbf{w}$。而对于任意的支持向量，都有 $y_{i}f({\mathbf{x}}_i)=1$，所以只要代入任意一个支持向量，即可求出 $b$。在现实中，我们常用一种更鲁棒性的做法：使用所有支持向量求出的 $b$ 的平均值。