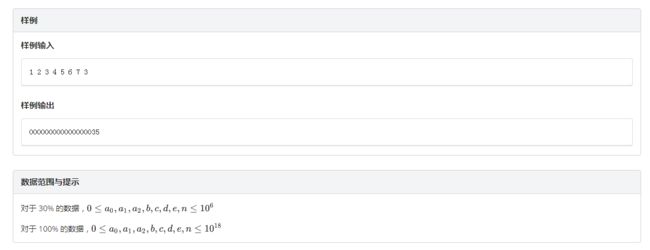
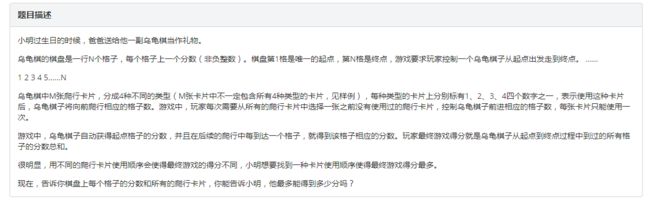
A、数列
题目描述
分析
非常显然的矩阵快速幂
首先我们要构造如下的两个矩阵
\(\left[ \begin{matrix} b &c &d &1\\1 &0 &0 &0\\ 0 &1 &0 &0\\0 &0 &0 &1\end{matrix} \right]\)
\(\left[ \begin{matrix} a_2 &0 &0 &0\\a_1 &0 &0 &0\\ a_0 &0 &0 &0\\e &0 &0 &0\end{matrix} \right]\)
然后做矩阵乘法就可以了
要注意的是,矩阵乘法不满足交换律,所以哪一行哪一列相乘一定要搞清
而且比较恶心的是,由于模数为\(10^{18}\),所以两个数相乘会爆\(long long\),因此在做乘法的时候还要用到高精度
考试的时候写完矩阵快速幂又写了一个暴力的对拍,却一直出错
后来输出中间变量才发现是暴力溢出了,最后5分钟才交上
代码
#include
using namespace std;
typedef unsigned long long ll;
const ll mod=1000000000000000000;
struct jz{
ll sz[10][10];
jz(){
memset(sz,0,sizeof(sz));
}
}now,ans;
ll jla[100],jlb[100],jg[100];
ll wdcf(ll aa,ll bb){
memset(jla,0,sizeof(jla));
memset(jlb,0,sizeof(jlb));
ll cnta=0,cntb=0;
while(aa){
jla[++cnta]=aa%10;
aa/=10;
}
while(bb){
jlb[++cntb]=bb%10;
bb/=10;
}
memset(jg,0,sizeof(jg));
for(ll i=1;i<=cnta;i++){
for(ll j=1;j<=cntb;j++){
jg[i+j-1]+=jla[i]*jlb[j];
}
}
ll mans=0,jl=1;
for(ll i=1;i<=19;i++){
if(jg[i]>=10){
ll zj=jg[i]/10;
jg[i+1]+=zj;
jg[i]%=10;
}
mans+=jg[i]*jl;
jl*=10;
}
return mans;
}
jz cf(jz aa,jz bb){
jz cc;
memset(cc.sz,0,sizeof(cc.sz));
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
for(int k=1;k<=4;k++){
cc.sz[i][j]=(cc.sz[i][j]%mod+wdcf(aa.sz[i][k],bb.sz[k][j])%mod)%mod;
}
}
}
return cc;
}
int num[50],cnt=0;
int main(){
ll a0,a1,a2,b,c,d,e,n;
scanf("%llu%llu%llu%llu%llu%llu%llu%llu",&a0,&a1,&a2,&b,&c,&d,&e,&n);
ans.sz[1][1]=a2%mod;
ans.sz[2][1]=a1%mod;
ans.sz[3][1]=a0%mod;
ans.sz[4][1]=e%mod;
now.sz[1][1]=b%mod;
now.sz[1][2]=c%mod;
now.sz[1][3]=d%mod;
now.sz[1][4]=1;
now.sz[2][1]=1;
now.sz[3][2]=1;
now.sz[4][4]=1;
ll jg;
if(n==0) jg=a0;
else if(n==1) jg=a1;
else if(n==2) jg=a2;
else {
ll zs=n-2;
while(zs){
if(zs&1) ans=cf(now,ans);
now=cf(now,now);
zs>>=1;
}
jg=ans.sz[1][1]%mod;
}
while(jg){
num[++cnt]=jg%10;
jg/=10;
}
int dy=18-cnt;
for(int i=1;i<=dy;i++){
printf("0");
}
printf("%llu\n",ans.sz[1][1]%mod);
return 0;
}
B、旗木双翼
题目描述
分析
很有思维含量的一道题
我们可以把题意转换成一个人从坐标为\((n,m)\)的开始走,走到坐标为\((0,0)\)的点
而且只能向上向右走的方案数
看下面的图可能会更好理解一些

因此最终的结果就是\(C_{n+m}^{n}\)
因为结果要取模,而且涉及到除法运算,因此要求逆元
代码
#include
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=200005;
ll ny[maxn];
int main(){
ll n,m;
scanf("%lld%lld",&n,&m);
ny[1]=1;
for(ll i=2;i<=n+m;i++){
ny[i]=(mod-mod/i)*ny[mod%i]%mod;
}
ll ans=1;
for(ll i=1;i<=n+m;i++){
ans=ans*i%mod;
}
for(ll i=1;i<=n;i++){
ans=ans*ny[i]%mod;
}
for(ll i=1;i<=m;i++){
ans=ans*ny[i]%mod;
}
printf("%lld\n",ans%mod);
return 0;
}
C、乌龟棋
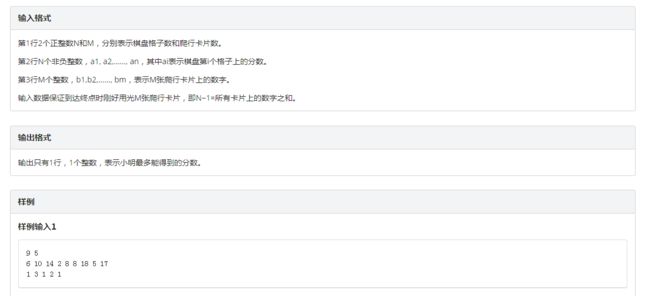
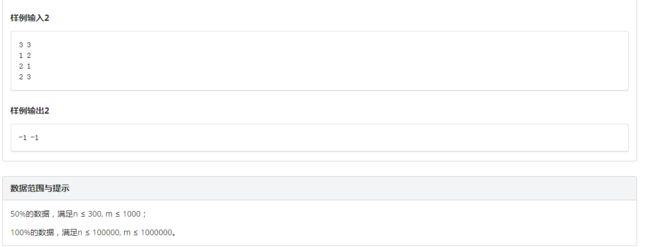
题目描述
分析
我们设\(f[a][b][c][d]\)为使用了\(a\)张标有数字\(1\)的卡片,\(b\)张标有数字\(2\)的卡片,\(c\)张标有数字\(3\)的卡片,\(d\)张标有数字\(4\)的卡片所能得到的最大得分
状态转移方程就很显然了
代码
#include
using namespace std;
const int maxn = 45;
int f[maxn][maxn][maxn][maxn];
const int N = 400;
int nn[N],mm[N];
int n,m;
int sum[maxn];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
scanf("%d",&nn[i]);
}
for(int i=1;i<=m;++i){
scanf("%d",&mm[i]);
sum[mm[i]]++;
}
for(int a=0;a<=sum[1];++a){
for(int b=0;b<=sum[2];++b){
for(int c=0;c<=sum[3];++c){
for(int d=0;d<=sum[4];++d){
int jl1=0,jl2=0,jl3=0,jl4=0;
if(a)jl1=f[a-1][b][c][d];
if(b)jl2=f[a][b-1][c][d];
if(c)jl3=f[a][b][c-1][d];
if(d)jl4=f[a][b][c][d-1];
f[a][b][c][d]=max(max(jl1,jl2),max(jl3,jl4))+nn[a+2*b+3*c+4*d+1];
}
}
}
}
printf("%d\n",f[sum[1]][sum[2]][sum[3]][sum[4]]);
return 0;
}
D、假面舞会
题目描述
分析
传送门
代码
#include
using namespace std;
const int maxn=1e6+5;
int head[maxn],tot=2;
struct asd{
int from,to,next,val;
}b[maxn];
void ad(int aa,int bb,int cc){
b[tot].from=aa;
b[tot].to=bb;
b[tot].next=head[aa];
b[tot].val=cc;
head[aa]=tot++;
}
bool vis[maxn];
int dis[maxn],ans;
void DFS(int now){
vis[now]=1;
for (int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(!vis[u]){
dis[u]=dis[now]+b[i].val;
DFS(u);
} else {
if(ans==0) ans=abs(dis[now]+b[i].val-dis[u]);
else ans=__gcd(ans,abs(dis[now]+b[i].val-dis[u]));
}
}
}
int mmin,mmax;
int jud[maxn];
void dfs(int now){
mmax=max(mmax,dis[now]);
mmin=min(mmin,dis[now]);
vis[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
if(!jud[i]){
jud[i]=jud[i^1]=1;
int u=b[i].to;
dis[u]=dis[now]+b[i].val;
dfs(u);
}
}
}
int main(){
memset(head,-1,sizeof(head));
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int aa,bb;
scanf("%d%d",&aa,&bb);
ad(aa,bb,1);
ad(bb,aa,-1);
}
for(int i=1;i<=n;i++){
if(!vis[i]) DFS(i);
}
if(ans){
if(ans<3) printf("-1 -1\n");
else {
int now;
for(int i=3;i<=ans;i++){
if(ans%i==0) {
now=i;
break;
}
}
printf("%d %d\n",ans,now);
}
return 0;
}
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++){
if(!vis[i]){
mmin=mmax=dis[i]=0;
dfs(i);
ans+=mmax-mmin+1;
}
}
if(ans>=3) printf("%d 3\n",ans);
else printf("-1 -1\n");
return 0;
}