配合上一篇效果更佳--->字符串学习笔记一
4.0 四、字典树
定义
字典树又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
实现
从百度百科瞟的图
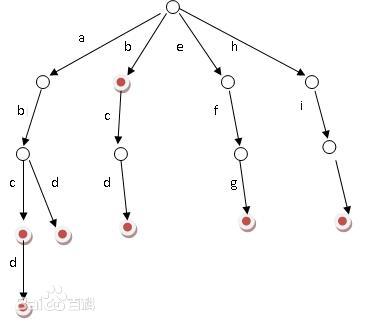
字典树一般用一个二维数组定义,\(tr[now][t]\)表示\(now\)节点的字符为\(t\)的儿子的编号
同时我们还要开一个数组\(cnt[now][t]\)表示该节点的个数
在某些情况下,我们还要记录有几个字符串在该节点终结、该节点属于第几个字符串等等
一般来说,字典树支持两种操作:插入和查询
假如要插入某个单词
一开始我们位于根节点,也就是\(0\)号节点
接下来我们判断根节点是否有某一个儿子\(ch\)
即\(tr[now][ch]\)是否等于\(0\)
如果等于\(0\),那我们再新开一个节点,否则把该节点的个数加一
查询操作也是如此,我们就从根节点一路走下去
如果可以走完,说明该单词存在,否则该单词不存在
代码实现
以洛谷P2922为例
#include
using namespace std;
const int maxn=2e7+5;
char c[maxn];
int tr[maxn][3],cnt[maxn][3],tot,ed[maxn][3];
void ad(char s[]){
int len=strlen(s);
int now=0;
for(int i=0;i 5.0 五、习题总结
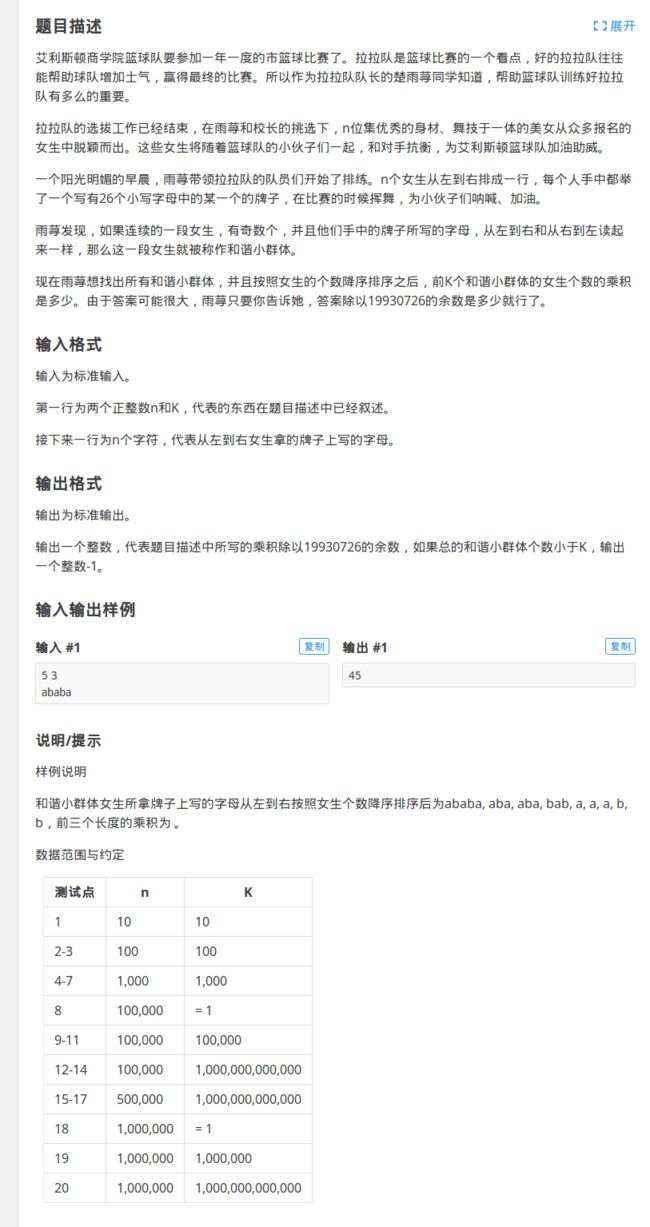
洛谷 P1659 [国家集训队]拉拉队排练
题目描述
分析
这一道题的大致意思就是让你求出一个字符串中所有的奇回文串,并把它们的长度连乘
考虑到求回文串,我们要使用\(manacher\)算法
因为题目中只让你求出奇回文串的个数,因此我们不用在原来的字符之间再插入特殊字符
在进行求解的时候,我们要使用一个\(p[i]\)数组记录以\(i\)为中心的最大回文半径的长度
而对于一个位置\(i\),如果向两边扩展\(p[i]\)是一个回文串,那么向两边扩展\(p[i]-k(p[i]-k\geq 1)\)也是一个回文串
因此,我们就可以求出以\(i\)为中心的所有回文半径的长度
但是,如果我们使用\(for\)循环直接遍历,必定会超时
因此,我们可以使用差分数组解决这一个问题,即在\(1\)的位置加一,在\(2 \times p[i] -1\)的位置减一
最后\(O(n)\)扫一遍即可
还有要注意的一点是,在进行乘法的时候,因为\(k\)的范围很大,所以要使用快速幂
代码
#include
using namespace std;
#define int long long
const int maxn=1e6+5;
char s[maxn];
int p[maxn],k,len,cf[maxn];
const int mod=19930726;
int ksm(int ds,int zs){
int ans=1;
while(zs){
if(zs&1) ans=ans*ds%mod;
ds=ds*ds%mod;
zs>>=1;
}
return ans;
}
signed main(){
scanf("%lld%lld",&len,&k);
scanf("%s",s+1);
s[0]='$';
for(int i=1,r=0,mids=0;i<=len;i++){
if(i<=r) p[i]=min(p[2*mids-i],r-i+1);
while(s[i-p[i]]==s[i+p[i]]) p[i]++;
if(p[i]+i>r) r=p[i]+i-1,mids=i;
cf[1]++,cf[p[i]*2]--;
}
for(int i=1;i<=len;i++){
cf[i]=cf[i-1]+cf[i];
}
int mans=1,tot=len;
if(tot%2==0) tot--;
while(k>0 && tot>0){
mans=mans*ksm(tot,min(cf[tot],k))%mod;
k-=cf[tot];
tot-=2;
}
if(k>0) printf("-1\n");
else printf("%lld\n",mans);
return 0;
}
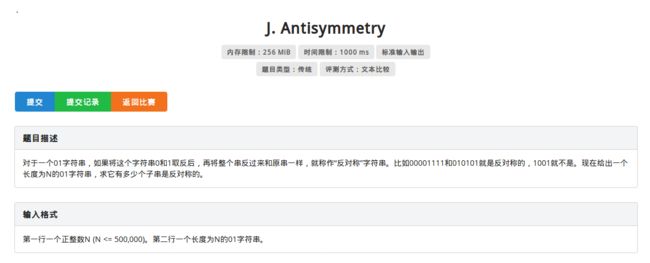
SP15569 STC02 - Antisymmetry
题目描述
分析
题意:对于一个只含有\(0\)和\(1\)的字符串,求出其在异或意义下的回文字串的数量
比较裸的\(manacher\),将判断的条件稍微改一下即可
代码
#include
using namespace std;
const int maxn=1e6+5;
char s1[maxn],s[maxn];
int f[maxn];
int main(){
int n;
scanf("%d",&n);
scanf("%s",s1+1);
s[0]='*';
int cnt=2*n+1;
for(int i=1;i<=cnt;i++){
if(i&1) s[i]='%';
else s[i]=s1[i/2];
}
int ans=0,mids=0,r=0;
for(int i=1;i<=cnt;i++){
if(i<=r) f[i]=min(f[2*mids-i],r-i+1);
while( ( (i-f[i])%2==0 && ( ((s[i+f[i]]-'0')^(s[i-f[i]]-'0')==1) ) )|| ( (i-f[i])%2==1 && (s[i-f[i]]==s[i+f[i]]) ) ) f[i]++;
if(i+f[i]>r) r=i+f[i]-1,mids=i;
if(i%2==1)ans+=((f[i]-1)/2);
}
printf("%d\n",ans);
return 0;
}
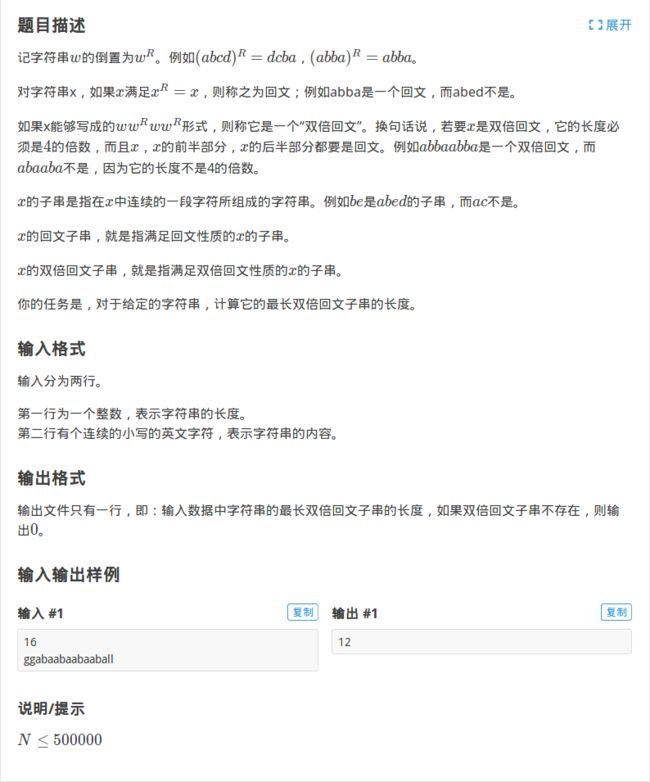
[SHOI2011]双倍回文
题目描述
分析
巧妙地利用了\(manacher\)算法的性质,即通过对称性查找回文字串
代码
#include
using namespace std;
const int maxn=2e6+15;
char s1[maxn],s[maxn];
int f[maxn];
int main(){
int n;
scanf("%d",&n);
scanf("%s",s1+1);
s[0]='*';
int cnt=2*n+1;
for(int i=1;i<=cnt;i++){
if(i&1) s[i]='%';
else s[i]=s1[i/2];
}
int ans=0,mids=0,r=0;
for(int i=1;i<=cnt;i+=2){
if(i<=r) f[i]=min(f[2*mids-i],r-i+1);
while(s[i+f[i]]==s[i-f[i]]) f[i]++;
if(i+f[i]-1>r) r=i+f[i]-1,mids=i;
if(i