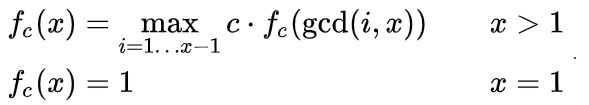2020牛客多校联赛第四场 （BFH）

B：Basic Gcd Problem

题目

翻译

例子

输入
2
3 3
10 5

输出
3
25

大意

给定一个函数

给你x和c，问这个函数的值是多少?

思路

举个例子:f(8)的最大值为 f(8) = c * f(gcd(8,4) == 4)，那么f(4) = c * f(gcd(4,2) == 2) ， f(2) = c * f(gcd(2,1) == 1) = c
综上:max f(8) = c * c * c

这个函数的递归退出条件就是gcd(i,x) == 1的时候，这时的f(1) = 1，那么既然退出递归的时候f(x)的值是定值1，那么最大值的影响关键就是递归的长度了换句话来说，递归得越久，那么乘c的次数就越多 。
因为f(x)的值是与gcd相关的，·所以我们分解x的质因子数量就可以了。为什么这样做呢?既然要递归得越长，那么我们就要充分的去利用他质因子，把每一个质因子利用起来，就可以得到最长的递归次数。

这里也举个例子叭，
8 = 2 * 2 * 2，那么就可以递归3次，第一次 8 = 4 * 2，所以gcd(8,4)，这样就利用了一个质因子2，依次类推。
借鉴于以下博客：
原文链接：https://blog.csdn.net/moasad/article/details/107463673

代码

#include 

using namespace std;

const int N = 1e6 + 5;
const int mod = 1e9+7;
typedef long long ll;
int arr[N],t;

ll quick_pow(ll a,ll b)
{
    ll ans = 1;
    while(b)
    {
        if(b&1)
            ans = a*ans%mod;
        b>>=1;
        a = a*a%mod;
    }
    return ans%mod;
}

signed main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    for(int i = 1;i <= N;i++)
    {
        int sum = 0,n = i;
        for(int j = 2;j * j <= n;j++)
        {
            while(n % j == 0)
            {
                sum++,n/=j;
                if(arr[n] != 0)
                {
                    arr[i] = arr[n] + sum;n = 0;
                    break;
                }
            }
            if(n == 0) break;
        }
        if(n == 0) continue;
        if(n > 1) sum++;
        arr[i] = sum;
    }
    scanf("%d",&t);
    while(t--)
    {
        ll n,c;
        scanf("%lld %lld",&n,&c);
        printf("%lld\n",quick_pow(c,arr[n]));
    }
}

F：Finding the Order

题目

翻译

例子

输入
2
3 5 5 3
5 3 3 5

输出
AB // CD
AB // DC

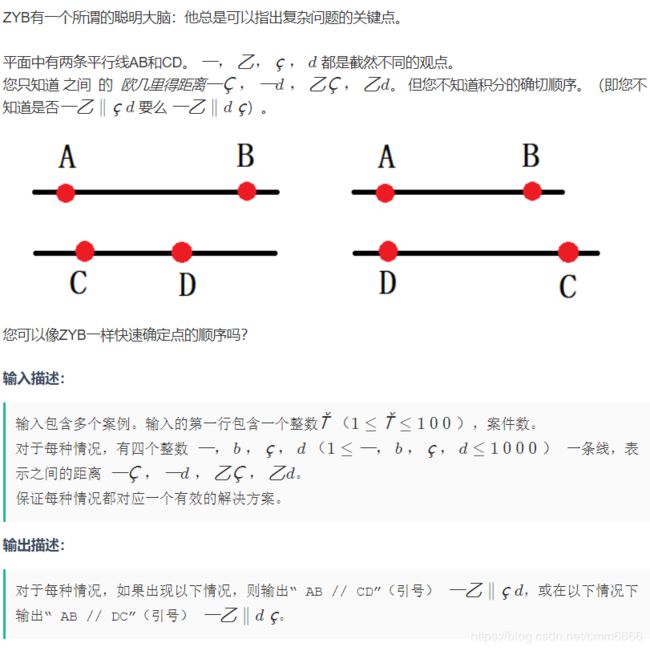
大意

有两条平行的线AB和CD，给出AC, AD, BC, BD 的长度，分别为a, b, c, d。问是AB//CD，还是AB//DC。

思路

证明：
∵OA+OD>AD,OB+OC>BC
∴(OA+OC)+(OB+OD)>AD+BC
∴AC+BD>AD+BC
∵OA+OD>AD,OB+OC>BC
∴(OA+OC)+(OB+OD)>AD+BC
∴AC+BD>AD+BC
所以只需要判断一下是否AC+BD>AD+BC即可。
技巧来源于以下博客：https://blog.nowcoder.net/n/ae72fbb6ebba4ca5a164bdc0d7b60e36

代码

#include

using namespace std;

int main()
{
    int t;
    cin>>t;
    while(t--){
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        puts(b+c>a+d?"AB//CD":"AB//DC");
    }
    return 0;
}

H：Harder Gcd Problem

题目

翻译

例子

输入
2
4
10

输出
1
2 4
4
3 9

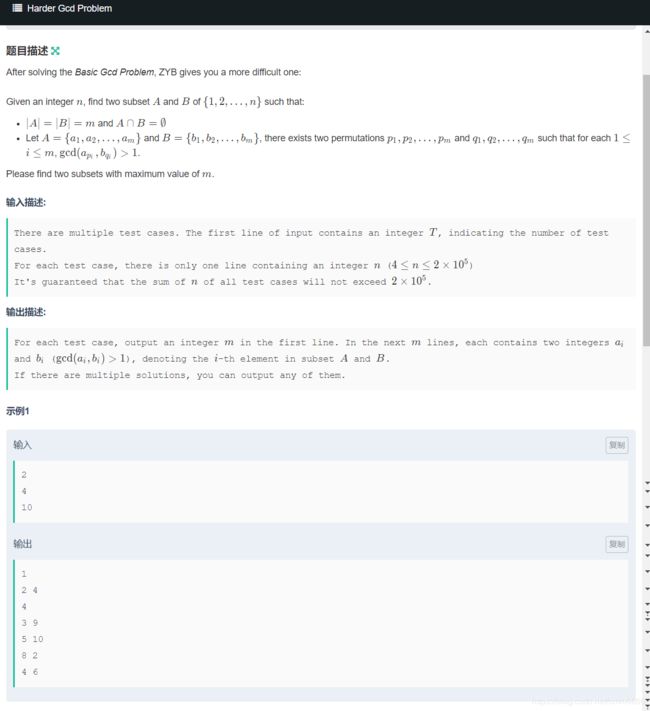
大意

集合A和B都是{1,2,…,n}的子集，A∩B≠∅。问A和B最多有多少对数GCD(Ap，Bq)>1。

思路

贪心。我们把n分解出质因数。不同质因数与它的倍数可以组成一对。所以我们只要枚举前n/2个质因数。
但是我们不能从小到大枚举每个质因数的倍数，因为有可能最大的质因数的与它的倍数无法组成一队
假设 n=8
质因数为 2,3,5,7.但我们只取2,3这两个质因数(因为5和7的倍数一定大于n)
2可以枚举的倍数分别为 2,4,6,8 那么可以组成2对 (2,4),(6,8)
3可以枚举的倍数分别为 3,6 这时候因为6被用了，所以不能组成一对 这样答案不一定最优了

所以我们需要贪心从大往小贪质因数。对于每个质因数p可以枚举倍数的个数为x 如果x为奇数，我们把 2*p留下来，等待后续匹配
举个例子n=9
质因数为2,3,5,7 我们只取2,3
3可以枚举的倍数分别为3,6,9 根据上述我们要把6留下来 所以(3,9)匹配
2可以枚举的倍数分别为2,4,6,8 根据上述我们可以组成(2,6),(4,8）6留下来就是现在匹配的

原文链接：https://blog.csdn.net/qq_43690454/article/details/107474284

代码

#include
using namespace std;
const int N=2e5+10000;
int prime[N],cnt,t,n;
int num[N];
bool st[N];
void init()
{
	memset(st,false,sizeof st);
	for(int i=2;i<N;i++)
	{
		if(!st[i]) prime[++cnt]=i;
		for(int j=1;j<=cnt&&prime[j]<=N/i;j++){
			st[prime[j]*i]=true;
			if(i%prime[j]==0) break;
		}
	}
	 
} 
int main()
{
	init();
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++) st[i]=false;
		memset(num,0,sizeof num);
		int tot=0;
		int mx=upper_bound(prime+1,prime+1+cnt,n/2)-prime-1;
		for(int i=mx;i>=1;i--)
		{
			for(int j=prime[i];j<=n;j+=prime[i])
			{
				if(st[j]) continue;
				if(j==2*prime[i]) continue;
				num[++tot]=j;
				st[j]=true;
			}
			if(tot&1) num[++tot]=2*prime[i],st[2*prime[i]]=true;
		}
		printf("%d\n",tot/2);
		for(int i=1;i<=tot;i+=2) 
		{
			printf("%d %d\n",num[i],num[i+1]);
		}
	 } 
 }