并查集及其java实现

本文内容转载自 博客https://www.cnblogs.com/cyjb/p/UnionFindSets.html 代码部分根据左神在课上讲的内容所写，本文主要目的为个人记录。

并查集（Union-find Sets）是一种非常精巧而实用的数据结构，它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先（Least Common Ancestors, LCA）等。

使用并查集时，首先会存在一组不相交的动态集合 $S=\{S_1,S_2,\cdots ,S_k\}$，一般都会使用一个整数表示集合中的一个元素。

每个集合可能包含一个或多个元素，并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的，具体选择哪个元素作为代表一般也是不关心的。我们关心的是，对于给定的元素，可以很快的找到这个元素所在的集合（的代表），以及合并两个元素所在的集合，而且这些操作的时间复杂度都是常数级的。

并查集的基本操作有三个：

• makeSet(s)：建立一个新的并查集，其中包含 s 个单元素集合。
• unionSet(x, y)：把元素 x 和元素 y 所在的集合合并，要求 x 和 y 所在的集合不相交，如果相交则不合并。
• find(x)：找到元素 x 所在的集合的代表，该操作也可以用于判断两个元素是否位于同一个集合，只要将它们各自的代表比较一下就可以了。

并查集的实现原理也比较简单，就是使用树来表示集合，树的每个节点就表示集合中的一个元素，树根对应的元素就是该集合的代表，如图 1 所示。

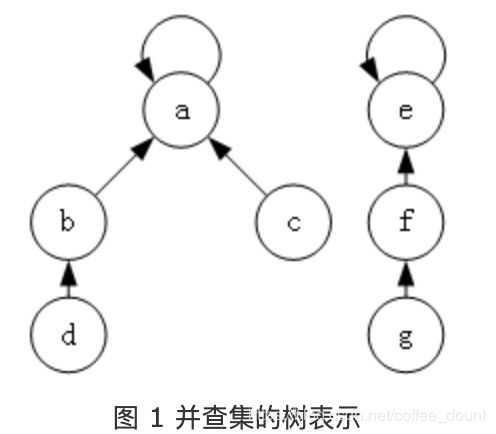
图中有两棵树，分别对应两个集合，其中第一个集合为 $\{a,b,c,d\}$，代表元素是 a；第二个集合为 $\{e,f,g\}$，代表元素是 e。

树的节点表示集合中的元素，指针表示指向父节点的指针，根节点的指针指向自己，表示其没有父节点。沿着每个节点的父节点不断向上查找，最终就可以找到该树的根节点，即该集合的代表元素。

现在，应该可以很容易的写出 makeSet 和 find 的代码了，假设使用hashmap来实现，那么 makeSet 要做的就是构造出如图 2 的森林，其中每个元素都是一个单元素集合，即父节点是其自身：

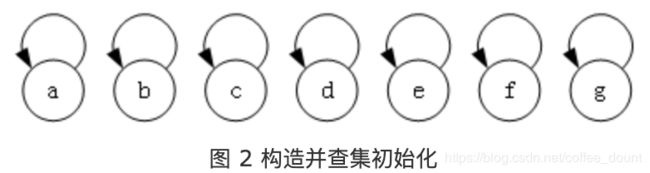
相应的代码如下所示，时间复杂度是$O(n)$：

public HashMap<Node, Node> fatherMap;//key:child   value:father
public HashMap<Node, Integer> sizeMap;//key:代表节点 value:该代表节点所代表的集合中的元素的数量   非代表节点可以不存该数据

public UnionFindSet() {
	fatherMap = new HashMap<Node, Node>();
	sizeMap = new HashMap<Node, Integer>();
}

public void makeSets(List<Node> nodes) {
	fatherMap.clear();
	sizeMap.clear();
	for (Node node : nodes) {
		fatherMap.put(node, node);
		sizeMap.put(node, 1);
	}
}

接下来，就是 find 操作了，如果每次都沿着父节点向上查找，那时间复杂度就是树的高度，完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。

路径压缩，就是在每次查找时，令查找路径上的每个节点都直接指向根节点，如图 3 所示。

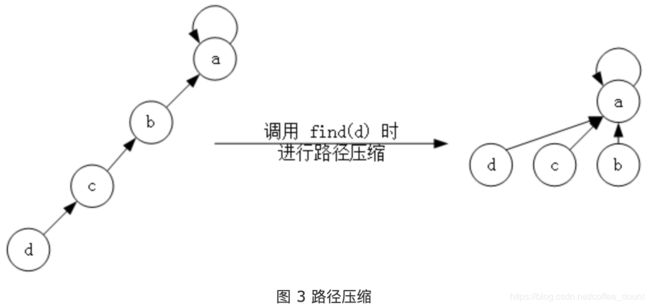
我准备了两个版本的 find 操作实现，分别是递归版和非递归版，不过两个版本目前并没有发现有什么明显的效率差距，所以具体使用哪个完全凭个人喜好了。

private Node findHead(Node node) {
	Node father = fatherMap.get(node);
	if (father != node) {
		father = findHead(father);
	}
	fatherMap.put(node, father);
	return father;
}

private Node findHead(Node node){
	Stack<Node> stack = new Stack<>();
	Node cur=node;
	Node parent=fatherMap.get(cur);
	while (cur!=parent){
		stack.push(cur);
		cur=parent;
		parent=fatherMap.get(cur);
	}
	while (!stack.isEmpty()){
		fatherMap.put(stack.pop(),parent);
	}
	return parent;
}

最后是合并操作 unionSet，并查集的合并也非常简单，就是将一个集合的树根指向另一个集合的树根，如图 4 所示。

这里按集合中包含的元素个数（或者说树中的节点数）合并，将包含节点较少的树根，指向包含节点较多的树根。

public void union(Node a, Node b) {
	if (a == null || b == null) {
		return;
	}
	Node aHead = findHead(a);
	Node bHead = findHead(b);
	if (aHead != bHead) {
		int aSetSize= sizeMap.get(aHead);
		int bSetSize = sizeMap.get(bHead);
		if (aSetSize <= bSetSize) {
			fatherMap.put(aHead, bHead);
			sizeMap.put(bHead, aSetSize + bSetSize);
		} else {
			fatherMap.put(bHead, aHead);
			sizeMap.put(aHead, aSetSize + bSetSize);
		}
	}
}

下面是按秩合并的并查集的完整代码，这里只包含了递归的 find 操作。

import java.util.HashMap;
import java.util.List;

public class UnionFind {

	public static class Node {
		// whatever you like
	}

	public static class UnionFindSet {
		public HashMap<Node, Node> fatherMap;
		public HashMap<Node, Integer> sizeMap;

		public UnionFindSet() {
			fatherMap = new HashMap<Node, Node>();
			sizeMap = new HashMap<Node, Integer>();
		}

		public void makeSets(List<Node> nodes) {
			fatherMap.clear();
			sizeMap.clear();
			for (Node node : nodes) {
				fatherMap.put(node, node);
				sizeMap.put(node, 1);
			}
		}

		private Node findHead(Node node) {
			Node father = fatherMap.get(node);
			if (father != node) {
				father = findHead(father);
			}
			fatherMap.put(node, father);
			return father;
		}
		
		public boolean isSameSet(Node a, Node b) {
			return findHead(a) == findHead(b);
		}

		public void union(Node a, Node b) {
			if (a == null || b == null) {
				return;
			}
			Node aHead = findHead(a);
			Node bHead = findHead(b);
			if (aHead != bHead) {
				int aSetSize= sizeMap.get(aHead);
				int bSetSize = sizeMap.get(bHead);
				if (aSetSize <= bSetSize) {
					fatherMap.put(aHead, bHead);
					sizeMap.put(bHead, aSetSize + bSetSize);
				} else {
					fatherMap.put(bHead, aHead);
					sizeMap.put(aHead, aSetSize + bSetSize);
				}
			}
		}
	}
}

并查集的空间复杂度是$O(n)$的，这个很显然，如果是按秩合并的，占的空间要多一些。find 和 unionSet 操作都可以看成是常数级的，或者准确来说，在一个包含 n 个元素的并查集中，进行 m 次查找或合并操作，最坏情况下所需的时间为 $O(m\alpha (n))$，这里的 α 是 Ackerman 函数的某个反函数，在极大的范围内（比可观察到的宇宙中估计的原子数量 1080 还大很多）都可以认为是不大于 4 的。具体的时间复杂度分析，请参见《算法导论》的 21.4 节 带路径压缩的按秩合并的分析。