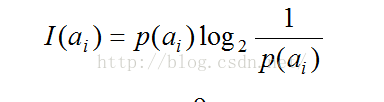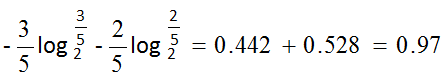决策树--ID3算法

一、决策树基本概念

      在机器学习中，决策树是一个预测模型，它代表的是对象属性与对象值之间的一种映射关系。本质上决策树是通

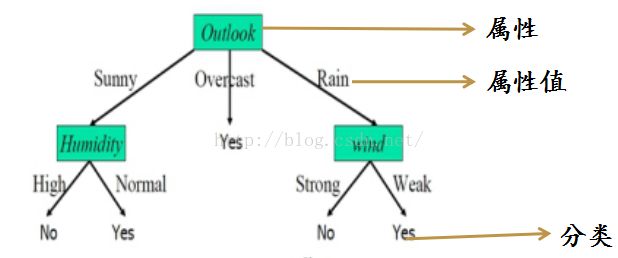
过一系列规则对数据进行分类的过程。下图为经典决策树实例。

                                         

                                                                           图1

        如图所示，实例是由“属性-值”对表示的：实例是用一系列固定的属性和他们的值构成。   

    
        目标函数具有离散的输出值：上图给每个实例赋予一个布尔型分类(Yes和No)。在实际的应用中，最后存储在分

类中的其实是一堆一堆的样本。

决策树的优点：

1、推理过程容易理解，决策推理过程可以表示成If Then形式；

2、可自动忽略目标变量没有贡献的属性变量，也为判断属性变量的重要性，减少变量的数目提供参考。

二、决策树的本质

      给定一堆样本，每个样本都有一组属性和一个类别，这些类别是事先确定的，那么通过学习得到一个分类器，这

个分类器能够对新出现的对象给出正确的分类。

三、决策树算法

       与决策树相关的重要算法：

          1、1979年, J.R. Quinlan 给出ID3算法，并在1983年和1986年对ID3 进行了总结和简化，使其成为决策树学习 

               算法的典型。

          2、Schlimmer 和Fisher 于1986年对ID3进行改造，在每个可能的决策树节点创建缓冲区，使决策树可以递增式                 生成，得到ID4算法。

        3、1988年，Utgoff 在ID4基础上提出了ID5学习算法，进一步提高了效率。

  4、1993年，Quinlan 进一步发展了ID3算法，改进成C4.5算法。

        当然还有其他很多的算法，我个人觉得最基本的依然是ID3和C.4.5算法。

 ID3 算法：

          ID3算法主要针对属性选择问题。是决策树学习方法中最具影响和最为典型的算法。为了衡量一个属性的好坏标

准，定义了一个统计属性，称为“信息增益”。

          该方法使用信息增益度选择测试属性。

          在介绍信息增益之前，需要引入一个信息论中的度量词--信息熵。

信息量和信息熵：

给定事件ai以及其概率P(ai)，其信息量可以如下表示：

                                         

为了精确的定义信息增益，采用了信息论中广泛使用的度量标准，称为信息熵。

假设有n个互不相容的事件 ,它们中有且仅有一个发生，则其平均的信息量可如下度量：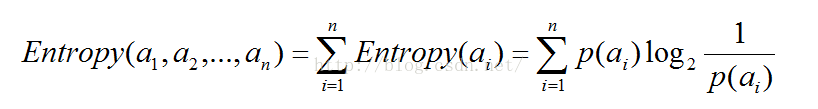

ID3 –信息增益：

在决策树分类中，信息增益表示的是由于使用这个属性分割样例而导致的期望熵的降低。

    比如A=outlook属性时，v属于{ sunny, overcast, rain }

   上图为经典打球案列的样例集。

   下面将会详细讲解具体是如何构建一颗决策树的。

1 选出outlook, Temperature, Humidity,Wind中信息增益最大的属性

该活动无法进行的概率是：5/14

该活动可以进行的概率是：9/14

因此样本集S的信息熵：

Entropy(S) =-5/14log(5/14) - 9/14log(9/14) = 0.940

 

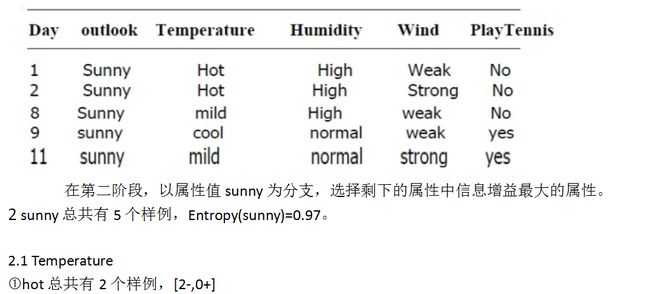
1.1 对于属性outlook来说，outlook = { sunny, overcast, rain }

         sunny总共有5个样例，其中[3-,2+]。

     其信息熵Entropy(sunny)=

                         

这样，一个决策树就被构建出来了。

这是决策树中最简单的一个算法，后面还有很多改进的算法。

本文是桂林电子科技大学的课程 数据挖掘与数据仓库 课后的总结。在课后，还有几个印象比较深刻的问题：

1、二位决策树的分裂面是什么样的？

2、什么样的属性才能被用来做相关属性？即相关属性的选择问题。

3、决策树可以由前面的属性推测出分类属性，由属性和分类属性能否推出前面的某一属性，比如，能否由Outlook、Humidity、Temperature和Playtennis推出Wind的属性值？