[机器学习-原理篇]支持向量机(SVM)深入理解
支持向量机SVM
- 1,SVM概念
- 1.1 支持向量机包含三种:
- 2.准备知识
- KKT条件
- 点到直线的距离
- 3. 线性可分支持向量机(hard margin)
- 线性可分支持向量机建立超平面:
- 函数间隔:
- 几何间隔:
- (1) 求 min w , b L ( w , b , α ) \large \mathop {\min }\limits_{w,b} L(w,b,\alpha ) w,bminL(w,b,α):
- (2) 求 min w , b L ( w , b , α ) \large \mathop {\min }\limits_{w,b} L(w,b,\alpha ) w,bminL(w,b,α) 对 α \large \alpha α 的极大值:
- 4. 线性支持向量机(soft margin)
- 5. 非线性支持向量机
- 核方法
1,SVM概念
支持向量机(Support Vector Machine,SVM)属于有监督学习模型,主要于解决数据分类问题。通常SVM用于二元分类问题,对于多元分类可将其分解为多个二元分类问题,再进行分类,主要应用场景有图像分类、文本分类、面部识别和垃圾邮件检测等领域。
1.1 支持向量机包含三种:
- 线性可分支持向量机:当训练数据线性可分时,可通过硬间隔最大化,学习一个线性的分类器,叫线性可分支持向量机,也称硬间隔支持向量机
- 线性支持向量机:当训练数据近似线性可分时,可通过软间隔最大化,也学习一个线性的分类器,叫线性支持向量机,也称为软间隔支持向量机
- 非线性支持向量机:当训练数据线性不可分时,通过使用核函数技巧及软间隔最大化,学习一个非线性的支持向量机
线性可分的数据就是代表这些数据能够用一条直线分开(二分类),如下图所示:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第1张图片](http://img.e-com-net.com/image/info8/3bc497c19f1846d1a697574717b29713.jpg)
近似线性可分的数据如下图所示,即绝大多数的样本都能被准确分类,只有少数样本出现错误:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第2张图片](http://img.e-com-net.com/image/info8/e290609a31324242b963e05c794d8ebf.jpg)
所以对软间隔和硬间隔的理解:当训练数据是线性可分的,能够找到一个平面百分百的将数据分类正确,此时训练数据到超平面的距离就叫做硬间隔(粗俗的讲就是实打实的距离);如果训练数据近似线性可分,同样可以找到一个超平面能够将绝大部分的数据分类正确,只有少数的样本分类错误,如果能容忍这种错误的存在,此时训练数据到超平面的距离就是软间隔(粗俗理解就是不在意这些细节)。简言之,硬间隔就是不能容忍错误分类点的存在,软间隔就是允许错误分类点的存在。
2.准备知识
KKT条件
对于具有等式和不等式约束的一般优化问题

KKT条件给出了判断 x ∗ x^* x∗是否为最优解的必要条件,即:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第3张图片](http://img.e-com-net.com/image/info8/2ac436fb77cc47ac9fd7da2bc34f6146.jpg)
KKT的推导过程可以看这里
点到直线的距离
有直线 A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0,点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)到该直线的距离为:
d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 (1) d = \frac{{\left| {A{x_0} + B{y_0} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }} \tag 1 d=A2+B2∣Ax0+By0+C∣(1)
即:
d = ∣ ( A , B ) ( x 0 y 0 ) + C ∣ ∣ ∣ ( A , B ) ∣ ∣ (2) d = \frac{|(A,B) \begin{pmatrix} x_0 \\ y_0 \end{pmatrix}+ C|}{||(A,B)||} \tag 2 d=∣∣(A,B)∣∣∣(A,B)(x0y0)+C∣(2)
如果数据是 n 维时,此时直线就变成了平面,用 w \large w w 表示平面的法向量得:
d = ∣ w x + b ∣ ∥ w ∥ (3) \large d = \frac{{ |wx + b|}}{{\left\| { w } \right\|}} \tag 3 d=∥w∥∣wx+b∣(3)
3. 线性可分支持向量机(hard margin)
定义:给定线性可分训练数据集,由数据集训练得到超平面为
w ∗ x + b ∗ = 0 w^*x+b^* = 0 w∗x+b∗=0
决策函数为
f ( x ) = s i g n ( w ∗ x + b ∗ ) f(x) = sign(w^*x+b^*) f(x)=sign(w∗x+b∗)
成为线性支持向量机。
线性可分支持向量机建立超平面:
给定训练数据集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . . ( x n , y n ) , y = { − 1 , + 1 } , y \large D = ({x_1},{y_1}),({x_2},{y_2})....({x_n},{y_n}),y = \{ - 1, + 1\},\large y D=(x1,y1),(x2,y2)....(xn,yn),y={−1,+1},y是标签,因为是二分类,取值只有-1,+1
![[机器学习-原理篇]支持向量机(SVM)深入理解_第4张图片](http://img.e-com-net.com/image/info8/2df23db00b4945a0a37e82a4de882855.jpg)
假设数据分布如上图所示,我们想找一条直线能够把数据分开,有无数条直线可以做到,但是这么多直线中选哪一个最好呢?
线性支持向量机的原理就是几何间隔最大化,从而确定这条直线,即上图中粗的黑线。
于SVM的超平面定义为: w x + b = 0 \large wx + b = 0 wx+b=0,其中 w \large w w是超平面的法向量, x \large x x为训练数据,由上文(3)式可知数据点到超平面的距离为(此处公式标号依然为3):
d = ∣ w x + b ∣ ∥ w ∥ (3) \large d = \frac{{ |wx + b|}}{{\left\| { w } \right\|}} \tag 3 d=∥w∥∣wx+b∣(3)
函数间隔:
如果此时我们想比较两个点 x 1 , x 2 \large x_1,\large x_2 x1,x2到超平面的距离,把 x 1 , x 2 \large x_1,\large x_2 x1,x2带入(3)式后发现分母都是相同的,所以想要比较两个点到平面的距离时,只需要比较分子就可以了。所以 ∣ w x + b ∣ \large |wx + b| ∣wx+b∣能够相对表示点到平面的远近,而 w x + b \large wx + b wx+b的符号与类别标签的符号是否一致表示了分类正确与否(因为在做分类时,带入数据点计算 f ( x ) = s i g n ( w x + b ) f(x) = sign(wx+b) f(x)=sign(wx+b),当 w x + b \large w x + b wx+b为正时 f \large f f 也为正,然后跟 x \large x x 对应的标签 y \large y y 对比,如果 f \large f f 和 y \large y y 的符号相同说明分类正确,否则分类错误)。所以可以用 y ( w x + b ) \large y(wx + b) y(wx+b)来表示分类的正确性,我们把 y ( w x + b ) \large y(wx + b) y(wx+b)称为函数间隔。
定义样本点 ( x i , y i ) \large (x_i, y_i) (xi,yi) 到超平面 ( w , b ) \large (w,b) (w,b) 的函数间隔为:
γ ^ i = y i ( w x i + b ) (4) \large {\widehat \gamma _i} = {y_i}(w{x_i} + b) \tag 4 γ i=yi(wxi+b)(4)
而对于整个数据集 D \large D D,我们选取所有样本点中最小的函数间隔作为整个数据集到超平面的函数间隔,即
γ ^ = min i = 1 , . . . , n γ ^ i \large \widehat \gamma = \mathop {\min }\limits_{i = 1,...,n} {\widehat \gamma _i} γ =i=1,...,nminγ i
几何间隔:
函数间隔衡量的是点到超平面的远近,但是无法决定所要选择的超平面是哪一个。因为当我们把 w \large w w 和 b \large b b 都扩大2倍,那么函数间隔也会跟着扩大2倍,但是超平面并没有发生改变,还是原来的超平面。所以需要对法向量加某些约束,对 w \large w w 使用L2范数进行规范化,使得间隔是确定的。
定义样本点 ( x i , y i ) \large (x_i, y_i) (xi,yi) 到超平面 ( w , b ) \large (w,b) (w,b) 的几何间隔为:
γ i = y i ( w ∥ w ∥ x i + b ∥ w ∥ ) (5) \large {\gamma _i} = {y_i}(\frac{w}{{\left\| w \right\|}}{x_i} + \frac{b}{{\left\| w \right\|}}) \tag 5 γi=yi(∥w∥wxi+∥w∥b)(5)
而对于整个数据集 D \large D D,我们选取所有样本点中最小的几何间隔作为整个数据集到超平面的几何间隔,即
γ = min i = 1 , . . . , n γ i \large \gamma = \mathop {\min }\limits_{i = 1,...,n} {\gamma _i} γ=i=1,...,nminγi
函数间隔和几何间隔的关系:
可以看出函数间隔和几何间隔的关系为:
γ = γ ^ ∥ w ∥ (6) \large {\gamma } = \frac{{{{\widehat \gamma }}}}{{\left\| w \right\|}} \tag 6 γ=∥w∥γ (6)
上文说了,我们找到了这个几何间隔之后,因为几何间隔 γ \large {\gamma } γ 是所有样本点中距离超平面最小的值,所有其他样本点距到超平面的距离肯定都不小于 γ \large {\gamma } γ,即
y i ( w ∥ w ∥ x i + b ∥ w ∥ ) ≥ γ \large {y_i}(\frac{w}{{\left\| w \right\|}}{x_i} + \frac{b}{{\left\| w \right\|}}) \ge \gamma yi(∥w∥wxi+∥w∥b)≥γ
注:其实这些几何间隔为 \large {\gamma } 就是支持向量。
同时我们希望能够找到一组 w , b \large w,b w,b 使这个几何间隔最大,即 max w , b γ \large \mathop {\max }\limits_{w,b} \gamma w,bmaxγ
s . t \large s.t s.t表示约束条件。
因为把(6)式带入(7)得:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第6张图片](http://img.e-com-net.com/image/info8/472f8acd525b4d6c843384799d4988b2.jpg)
由于函数间隔的取值对优化问题没有影响,因为无论函数间隔取值多少,最终我们想要找到的是 w , b \large w,b w,b,所以可以令函数间隔为1,即 γ ^ = 1 \large \widehat \gamma = 1 γ =1 。注意到最大化 1 ∥ w ∥ \large \frac{1}{{\left\| w \right\|}} ∥w∥1 就等于最小化 1 2 ∥ w ∥ 2 \large \frac{1}{2}{\left\| w \right\|^2} 21∥w∥2,所以优化问题转化成:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第7张图片](http://img.e-com-net.com/image/info8/755f65c26be54fb8acad2c5a7bf610f3.jpg)
注:这里我们令 γ ^ = 1 \large \widehat \gamma = 1 γ =1,也就意味着到超平面的距离为1的点都是支持向量,即下图中画圈的点,如下图所示:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第8张图片](http://img.e-com-net.com/image/info8/72b820ca794b4d0486b3b0094032d449.jpg)
最终问题转化成了在一个线性约束下的二次优化问题,采用拉格朗日乘子法:
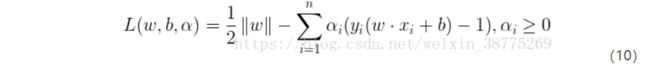
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 n α i ( 1 − y i ( w T x i + b ) ) (10) L(w,b,α)=\frac{1}{2}||w||^2+∑_{i=1}^nα_i(1-y_i(w^Tx_i+b)) \tag {10} L(w,b,α)=21∣∣w∣∣2+i=1∑nαi(1−yi(wTxi+b))(10)
现在需要最大化 L ( w , b , α ) \large L(w,b,\alpha ) L(w,b,α),所以问题变成 min w , b max α L ( w , b , α ) \large \mathop {\min }\limits_{w,b} \mathop {\max }\limits_\alpha L(w,b,\alpha ) w,bminαmaxL(w,b,α).
根据拉格朗日的对偶性,原始的极小极大问题变成了现在的极大极小问题 max α min w , b L ( w , b , α ) . \large \mathop {\max }\limits_\alpha \mathop {\min }\limits_{w,b} L(w,b,\alpha ). αmaxw,bminL(w,b,α).
(1) 求 min w , b L ( w , b , α ) \large \mathop {\min }\limits_{w,b} L(w,b,\alpha ) w,bminL(w,b,α):
让 L ( w , b , α ) \large L(w,b,\alpha ) L(w,b,α) 分别对 w , b \large w,b w,b 求偏导,使导数为 0:
{ ∂ L ( w , b , α ) ∂ w = = 0 ∂ L ( w , b , α ) ∂ b = 0 \begin{cases} \large \frac{{\partial L(w,b,\alpha )}}{{\partial w}} = = 0 \\ \large \frac{{\partial L(w,b,\alpha )}}{{\partial b}} = 0 \end{cases} {∂w∂L(w,b,α)==0∂b∂L(w,b,α)=0
得
{ w = ∑ i = 1 n α i y i x i ∑ i = 1 n α i y i = 0 (11) \begin{cases} \large w = \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{x_i}} \\ \large \sum\limits_{i = 1}^n {{\alpha _i}{y_i}} = 0 \end{cases} \tag {11} ⎩⎪⎪⎪⎨⎪⎪⎪⎧w=i=1∑nαiyixii=1∑nαiyi=0(11)
把式(11)带入式(10)得:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第9张图片](http://img.e-com-net.com/image/info8/eafd0ffb3de445f88b021494d9055d6d.jpg)
所以 min w , b L ( w , b , α ) = − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( x i x j ) + ∑ i = 1 n α i \large \mathop {\min }\limits_{w,b} L(w,b,\alpha ) = - \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}({x_i}{x_j})} } + \sum\limits_{i = 1}^n {{\alpha _i}} w,bminL(w,b,α)=−21i=1∑nj=1∑nαiαjyiyj(xixj)+i=1∑nαi
(2) 求 min w , b L ( w , b , α ) \large \mathop {\min }\limits_{w,b} L(w,b,\alpha ) w,bminL(w,b,α) 对 α \large \alpha α 的极大值:
问题变为: max α − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( x i x j ) + ∑ i = 1 n α i \large \mathop {\max }\limits_\alpha \ \ - \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}({x_i}{x_j})} } + \sum\limits_{i = 1}^n {{\alpha _i}} αmax −21i=1∑nj=1∑nαiαjyiyj(xixj)+i=1∑nαi
约束条件为: ∑ i = 1 n α i y i = 0 , α i ≥ 0 , i = 1 , 2... n \large \sum\limits_{i = 1}^n {{\alpha _i}{y_i}} = 0, \large {\alpha _i} \ge 0,i = 1,2...n i=1∑nαiyi=0,αi≥0,i=1,2...n
所以只要知道 α , w \large {\alpha },\large w α,w 也就知道了,假设最优解为 α ∗ = ( α 1 ∗ , α 2 ∗ . . . . α n ∗ ) T \large {\alpha ^ * } = {(\alpha _1^ * ,\alpha _2^ * ....\alpha _n^ * )^T} α∗=(α1∗,α2∗....αn∗)T
由式(11)可知 w ∗ = ∑ i = 1 n α i ∗ y i x i \large {w^ * } = \sum\limits_{i = 1}^n {\alpha _i^ * {y_i}{x_i}} w∗=i=1∑nαi∗yixi,假设此时得到的 b \large b b 的最优解为 b ∗ \large {b^ * } b∗,根据KKT条件可以得到:至少存在一个 α i ∗ > 0 \large \alpha _i^ *>0 αi∗>0 使:
α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 ) = 0 \large \alpha _i^ * ({y_i}({w^ * }\cdot {x_i} + {b^ * }) - 1) = 0 αi∗(yi(w∗⋅xi+b∗)−1)=0
反证法,假设 α ∗ = 0 \large \alpha ^ * =0 α∗=0 ,由式(11)可知 w ∗ = 0 \large w^*=0 w∗=0 ,而 w ∗ = 0 \large w^*=0 w∗=0时,
带入式(9)可得
y i b − 1 ≥ 0 (13) \large {y_i}b - 1 \ge 0 \tag{13} yib−1≥0(13)
因为 y i \large y_i yi 的取值只有+1和-1,要使上式成立, b \large b b 的取值是个不定值,说明超平面有多个,与原始问题矛盾,故至少存在一个 α j ∗ > 0 \large \alpha _j^ *>0 αj∗>0 ,对此 j \large j j 有:
α j ∗ ( y j ( w ∗ ⋅ x j + b ∗ ) − 1 ) = 0 , j = 1 , 2... n (14) \large \alpha _j^ * ({y_j}({w^ * }\cdot {x_j} + {b^ * }) - 1) = 0\ ,j=1,2...n \tag{14} αj∗(yj(w∗⋅xj+b∗)−1)=0 ,j=1,2...n(14)
因为 α j ∗ > 0 \large \alpha _j^ *>0 αj∗>0,所以可得:
( y j ( w ∗ ⋅ x j + b ∗ ) − 1 ) = 0 (15) \large ({y_j}({w^ * }\cdot {x_j} + {b^ * }) - 1) = 0 \tag{15} (yj(w∗⋅xj+b∗)−1)=0(15)
把式(11)带入式(15),因为 y i = { + 1 , − 1 } \large {y_i} = \{ + 1, - 1\} yi={+1,−1} ,所以 1 y i = y i \large \frac{1}{{{y_i}}} = {y_i} yi1=yi,进而得到:
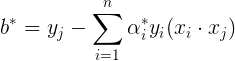
至此 w ∗ \large w^* w∗ 和 b ∗ \large b^* b∗ 都已经得到,
{ w ∗ = ∑ i = 1 n α i ∗ y i x i b ∗ = y j − ∑ i = 1 n a i ∗ y i ( x i x j ) \begin{cases} \large {w^ * } = \sum\limits_{i = 1}^n {\alpha _i^ * {y_i}{x_i}} \\ b^* = y_j - \sum\limits_{i = 1}^na_i^*y_i(x_ix_j) \end{cases} ⎩⎪⎪⎨⎪⎪⎧w∗=i=1∑nαi∗yixib∗=yj−i=1∑nai∗yi(xixj)
所以可以得到超平面: w ∗ ⋅ x + b ∗ = 0 \large {w^ * }\cdot x + {b^ * } = 0 w∗⋅x+b∗=0,
分类决策函数为: f ( x ) = s i g n ( w ∗ x + b ∗ ) \large f(x) = sign({w^ * }x + {b^ * }) f(x)=sign(w∗x+b∗)
注:其实由上面的式(15)可以看出,一定存在一些点使使(15)成立,即 y j ( w ∗ x j + b ∗ ) = 1 \large {y_j}({w^ * }{x_j} + {b^ * }) = 1 yj(w∗xj+b∗)=1,这个式子不就是代表函数间隔为1嘛,就是一定会存在支持向量,有了支持向量才能支撑起超平面。
上面我们只是假设已经求得了 α ∗ = ( α 1 ∗ , α 2 ∗ . . . . α n ∗ ) T \large {\alpha ^ * } = {(\alpha _1^ * ,\alpha _2^ * ....\alpha _n^ * )^T} α∗=(α1∗,α2∗....αn∗)T,
所以关键问题就是如何求 α ∗ \large \alpha ^* α∗ ,支持向量机中求 α ∗ \large \alpha ^* α∗的方法是SMO(Sequential Minimal Optimization)即序列最小最优化,感觉SMO其实不属于支持向量机算法的一部分,只是一种优化方法,所以没怎么着重看(手动捂脸),下面是自己的理解。
SMO的思想是因为拉格朗日乘子由许多个,即 α \large \alpha α 有许多个,每次只选择其中两个变量作为未知量,其他乘子作为已经量,将N个问题转变成两个变量的求解问题。比如对于线性可分支持向量机的目标函数:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第10张图片](http://img.e-com-net.com/image/info8/1981b57cea0d4274904a9513e1bb7ac8.jpg)
一开始选取两个变量 α 1 , α 2 \large {\alpha _1},{\alpha _2} α1,α2 作为未知量,其他因子 α i ( i = 3 , 4... n ) \large {\alpha _i}(i = 3,4...n) αi(i=3,4...n)当作已经的来求目标函数的最小值,求出 α 1 , α 2 \large {\alpha _1},{\alpha _2} α1,α2再带入进去,再选取 α 3 , α 4 \large {\alpha _3},{\alpha _4} α3,α4求目标函数最小值,求出后继续带入,直到所有 \large \alpha 都得到(中间过程其实挺复杂的,个人理解手动捂脸)。
4. 线性支持向量机(soft margin)
对于线性不可分的样本(有噪声干扰),可以适当放松边界超平面,以得到更好的鲁棒性能.soft margin形式下的SVM定义如下:
![[机器学习-原理篇]支持向量机(SVM)深入理解_第11张图片](http://img.e-com-net.com/image/info8/ee55c71af7e643a085b0b2a1a7459285.jpg)
其中, C C C为 ξ i ξ_i ξi的惩罚因子, C C C越大,对ξ的惩罚越大, ξ ξ ξ的可能取值越小,soft margin效果越弱,鲁棒性能越差,反之亦然.
5. 非线性支持向量机
核方法
定义: 在低维空间中不能线性分割的点集,通过转化为高维空间中的点集时,从而变为线性可分的,然后就可以应用线性分类学习方法从训练数据中学习分类模型,这就是核方法。
假如你有四个点如下图,你要把红色点和绿色点分开,但是你无法用一条线把它分开。只能用一条曲线分开
![[机器学习-原理篇]支持向量机(SVM)深入理解_第12张图片](http://img.e-com-net.com/image/info8/c80f293b31884e55a7e0846b49e152b4.jpg)
那么我们能不能把这个四个点找一个核函数把它映射到三维空间呢?
如图所示,这样就可以找到一个面把它分开了
![[机器学习-原理篇]支持向量机(SVM)深入理解_第13张图片](http://img.e-com-net.com/image/info8/2b4fb25e520b4ebda7c93b26d58d292c.jpg)
![[机器学习-原理篇]支持向量机(SVM)深入理解_第14张图片](http://img.e-com-net.com/image/info8/a117b421e6e443b8b8a85582e34ae879.jpg)
我们现在有三个等式 x + y , x y , x 2 x+y, xy, x^2 x+y,xy,x2. 那么这三个等式那个可以成功的分开它们呢?
通过表格的数据,显然 x y xy xy是最好的
![[机器学习-原理篇]支持向量机(SVM)深入理解_第15张图片](http://img.e-com-net.com/image/info8/8310dc9a291c480393067b48d250fbad.jpg)
所以我就可以用xy=1 来区分红色点和绿色点,xy=0 为红色的,xy=2为绿色的
![[机器学习-原理篇]支持向量机(SVM)深入理解_第16张图片](http://img.e-com-net.com/image/info8/b4a5b87a5e054a529020f60da666d03d.jpg)
Y = 1 x Y=\frac{1}{x} Y=x1其实就是这个图中的双曲线
![[机器学习-原理篇]支持向量机(SVM)深入理解_第17张图片](http://img.e-com-net.com/image/info8/4ed47c1933dc43389577c4edbecd7bfc.jpg)
那么我们用XY的值作为Z轴的值,把这个四个点映射到三维空间上,显然可以找到一个平面成功的区分它们了
![[机器学习-原理篇]支持向量机(SVM)深入理解_第18张图片](http://img.e-com-net.com/image/info8/783a5fc955ff4990b714db85be2e18c8.jpg)
参考资料
https://zhuanlan.zhihu.com/p/77750026?utm_source=wechat_session
https://blog.csdn.net/b285795298/article/details/81977271
https://blog.csdn.net/weixin_38775269/article/details/81839080
https://www.cnblogs.com/hello-ai/p/11332654.html
![[机器学习-原理篇]支持向量机(SVM)深入理解_第5张图片](http://img.e-com-net.com/image/info8/cbabf722c7874a5bb561d0c8a8f28f16.jpg)