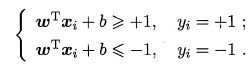SVM-支持向量机学习(1):线性可分SVM的基本型
1. foreword
先看的是李航老师的书第7章,比较传统按照以下三节展开:
- 线性可分SVM
- 线性SVM
- 非线性SVM
- SMO算法
李航老师讲东西向来不拖泥带水,但本节也几乎用了40页的篇幅,足见涉及内容之多。7月底硬着头皮啃了下来,边看边在笔记上摘抄标注,花了2天时间对SVM有了基本认识。一个月过去了,如今重新整理为博客,再看轻松许多,并不断对比西瓜书的内容,启望达到融会贯通。
西瓜书此节明显节奏轻快,花了2页引出SVM的概念和优化问题,压根没提什么函数间隔、几何间隔,按照最原始的理解展开。
2. 西瓜书如何引出SVM?
给定训练集 T={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{−1,+1} 。
分类学习最基本想法是:基于训练集在样本空间中找到一个划分超平面,将不同类别样本分开。由感知机一节可知,这样的超平面无穷多个。应该去找到哪个呢?
直观上,应该去找:位于两类样本正中间的划分超平面。即上图红色线。该超平面对训练样本局部扰动的容忍性最好。看那个黑线,正样本稍微动下就会被其分错,换言之,对样本局部扰动容忍性差。红色超平面产生的结果最鲁棒,对未见示例的泛化能力最强。
样本空间中,划分超平面可通过如下方程描述:
w为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离。
样本空间中,任意点 x 到超平面的距离为:
假设超平面可将训练样本正确分类:对于 yi=+1 ,有 wTx+b>0 , 对于 yi=−1 ,有 wTx+b<0 。我们令:
此处拐弯:为什么我们可以令其大于等于或小于等于1呢?不应该是0么?周老师在附注中解释:若超平面能将样本正确分类,则总存在缩放变换使得上式成立。此处周老师为了思路顺畅,并未展开。应参考李航老师书:系数缩放变换,则上述左侧值相应变,但超平面不变。不妨令其为1。
系数缩放可以想象:将图中一切放大,好像用放大镜看这个图。我们总能到一个合适的缩放使得函数间隔为1。几何间隔是原本的不变的。
如下图所示,距离超平面最近的几个训练样本使得上式的等号成立。被称为“支撑/支持向量”。每个样本点对应一个支撑向量。
两个异类支撑向量到超平面的距离之和,叫做间隔(margin):
我们要找到最大间隔的划分超平面,也就是要找到求解下列问题:
间隔貌似仅与w相关,实际上b通过约束隐式的影响w的取值,从而影响到间隔。
其可等价于(上式最大化,分母最小化,可平方最小化,为求导方便乘个1/2)
这就是支持向量机的基本型。(针对后面的对偶型)
3. 李航老师如何引入SVM?
看完周老师的讲解,再来看李老师的,便更有感觉。
李老师上来先是如传统授课方式那样,列出总纲。
3.1 引言
SVM:二类分类模型,其基本模型是定义在特征空间上的间隔最大(区别于感知机)的线性分类器。
SVM的学习策略:间隔最大化。
形式化:求解凸二次规划问题(convex quadratic programming)。
等价为:正则化的合页损失函数的最小化问题。
SVM的学习算法:求解凸二次规划的最优化算法。
学习内容:
- 1.线性可分SVM:数据线性可分时,硬间隔最大化,又称硬间隔SVM
- 2.线性SVM:数据近似线性可分时,软间隔最大化,又称软间隔SVM
- 3.非线性SVM:数据线性不可分时,核技巧,转化为软间隔SVM
核技巧:使得SVM成为实质上的非线性分类器。
输入为欧式空间(如常用的二维平面,三维立体空间)或离散空间时,特征空间为希尔伯特空间(向量是其中元素)时,核函数表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。而对偶形式中恰好求解向量间内积,直接替换即可。核函数的巧妙之处,不需要显示知道映射函数,只需要内积。
用核函数可学习非线性SVM,等价于隐式地在高维特征空间中学习线性SVM。这样的方法称为核技巧(kernel trick)。核方法是比SVM更为一般的ML方法。SVM可看作是核函数为 x−>x 映射的核技巧,特例。
引言完。先上来给你说个框架,然后再一步步讲细节。适合回味看。
3.2 SVM基本模型
线性SVM:假设输入空间与特征空间的元素直接一一对应,将输入空间的输入映射为特征空间中的特征向量。
非线性SVM:利用一个从输入空间到特征空间的非线性映射,来将输入映射为特征向量。
所以输入都由输入空间转换到特征空间,SVM的学习在特征空间中进行。
给定训练集 T={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{−1,+1} 。假设训练集是线性可分的,则存在无穷多个分离超平面将两类数据分开。
- 感知机:误分类个数最小的策略,求分离超平面,解有无穷多个。
- SVM:间隔最大化,解是唯一的。(泛化能力最强的那个超平面)
感知机训练时,误分类个数最小即可(转化为值大于0),衡量上较粗。而SVM使用距离,将误分类误差细化(值大于1)。不同分离超平面,误分类个数可能是相同的,但误分类距离绝对不同,SVM找出那个最大的。
定义
给定线性可分数据集,通过间隔最大化,等价求解相应的凸二次规划问题,学习得到的分离超平面为 w∗⋅x+b∗=0 。以及相应的分类决策函数为 f(x)=sign(w∗⋅x+b∗) 。这就是线性可分SVM。
对平面 w∗⋅x+b∗=0 来说,一个点到该平面的距离为:
因为w是相同的,所以可以用 |w⋅x+b| 相对表示点x距离超平面的远近。见下图关系,用三角形的斜边代替直角边:
点到超平面的距离的远近,可以看成是分类预测的确信程度。离得越远,说明分类器越自信,离得越近,说明分类器有点迷糊。
(w⋅x+b) 与 y 的符号是否一致,可表示分类是否正确。则 y⋅(w⋅x+b) 可表示分类的正确性(符号大于0即正确),以及确信度(值的大小)。
定义
超平面(w,b)关于样本点 (xi,yi) 的函数间隔为
超平面(w,b)关于训练集T的函数间隔为
即先算出所有样本点的函数间隔,然后取最小的作为训练集的函数间隔。
若成比例的改变w和b,超平面不变。但函数间隔按上式计算出来成倍变化。(可理解为用放大器看图的感觉)。所以我们对超平面的法向量w加约束,间隔可确定。此时函数间隔变成几何间隔。
定义
超平面(w,b)关于样本点 (xi,yi) 的几何间隔为
超平面(w,b)关于训练集的几何间隔为
此时计算式的系数实际上将法向量变成单位向量,归一化了。
再宏观看,几何间隔就是点到直线的距离。
从这里入手讲,是很顺的
SVM学习的基本想法:求解可正确划分T并且几何间隔最大的分离超平面。(最迷糊的距离尽可能长)
间隔最大化的直观解释:对T找到几何间隔最大的(w,b),意味着以充分大的置信度对T分类,不仅将正负样本分开,且对最难分的实例点(离超平面最近的点)也有足够大的确信度将其分开。
将其表述为数学形式:
约束表示:我们要找的超平面需要将所有样本点分开,几何间隔至少是r
目标表示:需要在其中找到一个最大的几何间隔
如上左图,黑线的几何间隔为1,红线的几何间隔为1.5,则选择红线作为最终的超平面。w,b不同,超平面不同,几何间隔不同,则迭代求解一个使得几何间隔最大(w,b)。
根据几何间隔和函数间隔的关系:
将上述问题转化为:
注意,下面处理是人为做的限制。函数间隔 r^ 对最优化问题的解并不影响。因为系数变倍,超平面不变,函数间隔随之变倍,对任何系数,总可以缩放使得函数间隔为1。不妨令 r^=1 。
对应着周老师的令:
其可等价于(上式最大化,分母最小化,可平方最小化,为求导方便乘个1/2)
上面是一个凸二次规划问题。
凸优化问题:约束最优化问题
minwf(w)s.t.gi(w)≤0hi(w)=0
f(w)和g(w)是连续可微凸函数,h(w)是仿射函数。
若f(x)满足f(x)=ax+b,即为仿射函数。
当f(w)是二次函数且g(w)是仿射函数时,称为凸二次规划问题。
算法:线性可分SVM的学习算法:间隔最大法
- 输入:T,二分类
- 输出:最大间隔分离平面,分类决策函数
- 过程:
- 构造求解约束最优化问题:凸二次规划问题
- 求出最优解
- 得到分离超平面和分类决策函数
李老师书P101证明:最大间隔分离超平面存在且唯一存在。不再赘述在此。
P33页感知机时证明:线性可分的数据集上,误分类次数的是有上界的,即迭代是收敛的。
如下图所示,距离超平面最近的几个训练样本使得上式的等号成立。被称为“支撑/支持向量”。每个样本点对应一个支撑向量。
两个异类支撑向量到超平面的距离之和,叫做间隔(margin):
图中的间隔边界是平行的。分离超平面位于中央。决定分离超平面时,只有支撑向量才起作用。这就是为何叫做支持向量机。支撑向量的个数较少,SVM由很少的重要的训练样本决定。
举一个例子:
已知 x1=(3,3),x2=(4,3),x3=(1,1),y1=y2=+1,y3=−1 ,求最大间隔分离超平面。(因x为2维,则w为2维)
解:由算法构造约束最优化问题
最优解为 w1=w2=12,b=−2 。
超平面为 12x(1)+12x(2)−2=0
支撑向量为 x1=(3,3),x2=(1,1) 。
继续讨论:随便找个可行解(黑线),如 13x(1)+23x(2)−2=0 ,其满足约束的3个条件,但其 12(w21+w22)=518 ,大于最优解(红线)的 14 。