2019年秋季数据挖掘与机器学习课程学习笔记

第一节课

第二节课

第三节课

第四节课 density estimation

介绍：

令$X_1,X_2,...,X_n$是来自分布$P$的密度为$p$的样本，非参数密度估计目标就是在最少的关于密度$p$的假设的情况对$p$进行估计。我们用$\hat{p}$来表示$p$的估计。这个估计会依赖一个光滑的参数$h$，小心的选择$h$是关键的。为了强调这个对$h$的依赖，我们使用${\hat{p}}_h$记号。

密度估计可被用于：回归、分类、聚类、无监督预测。举例而言：如果$\hat{p}(x,y)$是$p(x,y)$的一个估计，那么我们可以得到回归函数的以下估计：
$$\hat{m}(x)=\int y\widehat{(}y|x)dy$$
其中$\hat{p}(y|x)=\hat{p}(y,x)\hat{p}(x)$.对于分类问题而言，我们回忆Bayes rule：
$$h(x)=I(p_1(x){\pi }_1>p_0(x){\pi }_0)$$
其中${\pi }_1=\mathbb{P}(Y=1),{\pi }_0=\mathbb{P}(Y=0),p_1(x)=p(x|y=1)$,$p_0(x)=p(x|y=0)$.输入样本对于${\pi }_1,{\pi }_0$的估计，对$p_1,p_0$的密度估计则会产生一个基于Bayes rule的预测。很多你熟悉的分类器可以被用这种方式重新表述。

损失函数

最常使用的损失函数是$L_2$损失：
$$\int (\hat{p}-p(x){)}^{2}dx=\int {\hat{p}}^2(x)dx-2\int \hat{p}(x)p(x)+\int p^2(x)dx$$
风险是 $R(p,\hat{p})=\mathbb{E}(L(p,\hat{p}))$。
Devroye and Gyorfi(1985) 强烈推荐使用 $L_1$范数
$$\Vert \hat{p}-p{\Vert }_1\equiv \int |\hat{p}(x)-p(x)|dx$$
作为$L_2$范数的代替。$L_1$损失有以下的良好解释：如果$P,Q$是分布，定义全变差度量：
$$d_{TV}(P,Q)=su{p}_A|P(A)-Q(A)|$$
上确界取遍所有的可测集。如果$P,Q$有密度$p,q$那么有：
$$d_{TV}(P,Q)=\frac{1}{2}\int |p-q|=\frac{1}{2}\Vert p-q{\Vert }_1$$
因此，如果$\int |p-q|<\delta$那么我们知道$|P(A)-Q(A)|<\frac{\delta }{2}$对于所有的$A$。同样的，$L_1$范数是一个变形不变量(transformation invariant)。假设$T$是一个一对一的光滑映射，令$Y=T(X)$。令$p$和$q$是$X$的密度，令$\hat{p},\hat{q}$是相应的$Y$的密度，那么：
$$\int |p(x)-q(x)|dx=\int |\hat{p}(y)-\hat{q}(y)|dy$$
因此在此定义下的距离不会因为一一映射而改变，但无论如何我们还是聚焦于$L_2$损失。

Histograms直方图

Perhaps the simplest density estimators are histograms. For convenience, assume that the data $X_1,...,X_n$ are contained in the unit cube $X=[0,1{]}^d$ (although this assumption is not crucial). Divide $\mathcal{X}$ into bins, or sub-cubes, of size $h$. We discuss methods for choosing $h$later.

Kernel Density Estimation核密度估计

一个一维的光滑核(smoothing kernel)是任意的一个光滑函数（其定义域内无穷阶数连续可导的函数）$K$满足$\int K(x)dx=1,$$\int xK(x)dx=0,{\sigma }_k^2\equiv \int x^{2}K(x)dx>0$。一些常用的核函数如下所示：
Boxcar:$K(x)=\frac{1}{2}I(x)$
Gaussian:$K(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$
Epanechnikov :$K(x)=\frac{3}{4}(1-x^2)I(x)$
Tricube:$K(x)=\frac{70}{81}(1-|x{|}^3{)}^{3}I(x)$
其中$I(x)=1$如果$|x|\le 1$。否则$I(x)=0$.这些核的图像如下，常用的多维的核是${\prod }_{j=1}^{d}K(x_j),K(\Vert x\Vert )$。


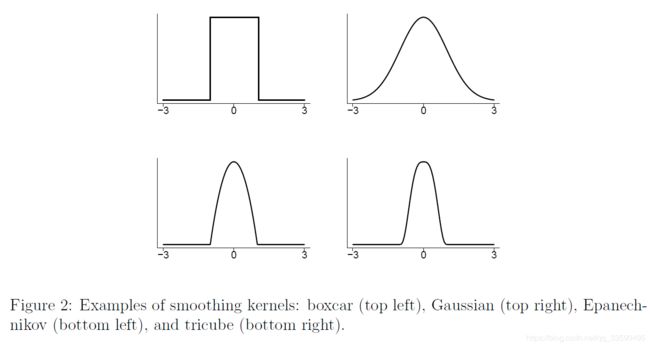
给定一个$X\in {\mathcal{R}}^d$。给定一个核$K$和一个正数$h$，称之为窗宽(bandwidth)，核密度的估计定义为：
$$\hat{p}(x)=\frac{1}{n}\sum _{i=1}^n{h}^{d}K(\frac{\Vert x-X_i\Vert }{h})$$
由上面示性函数的定义我们知道也就是说与$x$点的距离(范数)大于$h$的$X_i$将不会对$x$点处的密度有贡献。更一般的我们定义：
$${\hat{p}}_H(x)=\frac{1}{2}\sum _{i=1}^n{K}_H(x-X_i)$$
其中$H$是一个正数定义了窗宽矩阵(bandwidth matrix)以及$K_H=|H{|}^{-\frac{1}{2}}K(H^{-\frac{1}{2}}x)$，为了简化表达，我们令$H=h^{2}I$，然后我们得到先前的公式。

有时我们使用记号${\hat{p}}_h$来表达$\hat{p}$对width $h$的依赖性。在多元的情况下，每个样本的坐标$X_i$应当被标准化来使每个样本是同方差的，因为范数 $\Vert x-X_i\Vert$把所有的坐标看做它们是在同一度量下。

核估计对于每个数据点$X_i$都放置了一个size是$\frac{1}{n}$的质量块，见图3。核的形式选择没有$h$的选择关键。一个较小的$h$会带来一个粗糙的估计，一个较大的$h$会带来一个更光滑的估计。

4.1Risk Analysis

在这节中我们测试核密度的准确性，首先我们需要一些定义：
假设$X_i\in \mathcal{X}\subset {\mathbb{R}}^d$其中$\mathcal{X}$是紧集。令$\beta ,L$是正数。给定一个向量$s=(s_1,...,s_d)$，定义$|s|=s_1+...+s_d$，$s！=s_1!...s_d!$，$x^s=x_1^{s_1}...x_d^{s_d}$并且
$$D^s=\frac{{\partial }^{s_1+...+s_d}}{\partial x_1^{s_1}...\partial x_d^{s_d}}$$
令$\beta$是一个正整数。定义 Holder class：
$$\sum (\beta ,L)=\{g:|D^{s}g(x)-D^{s}g(y)|\le L\Vert x-y\Vert ,forallssuchthat|s|=\beta -1,andallx,y\}$$
举例而言，如果$d=1,\beta =2$也就意味着：
$$|g^{\prime }(x)-g^{\prime }(y)|\le L|x-y|,forallx,y$$
最常见的情况就是$\beta =2$，粗略来说这意味着函数被二阶导数限制。
如果$g\in \sum (\beta ,L)$那么$g(x)$和他的泰勒级数展开是接近的：
$$|g(u)-g_{x,\beta }(u)|\le L\Vert u-x{\Vert }^{\beta }$$
现在假设核$K$有形式$K(x)=G(x_1)...G(x_d)$其中$G$定义在$[-1,1],\int G=1,\int |G{|}^p<\infty$对任意的$p>1$都成立，$\int |t{|}^{\beta }|K(t)|dt<\infty ,\int t^{s}K(t)=0$对于所有的$s\le \lfloor \beta \rfloor$。
一个核函数的例子在$\beta =2$的情况下满足这些条件的是$G(x)=(3/4)(1-x^2)$对所有的$|x|<1$。构造一个满足$\int t^{s}K(t)dt=0$对所有$\beta >2$的核函数需要这个核函数可以取负值。
令$p_h(x)=\mathbb{E}[{\hat{p}}_h(x)]$。下一个引理提供了一个偏差$p_h(x)-p(x)$的界限。

引理 3

$\hat{p}$的偏差满足：
$$su{p}_{p\in \sum (\beta ,L)}|p_h(x)-p(x)|\le c{h}^{\beta }$$
对于某个c
证明：我们有：

第一项被$L{h}^{\beta }\int K(s)|s{|}^{\beta }$限制因为$p\in \sum (\beta ,L)$。第二项是0因为K的性质 $p_{x,\beta }(x+hv)-p(x)$是一个阶数为$\lfloor \beta \rfloor$的多项式（没有常数项）。
下面，我们来限制方差：

引理 4

${\hat{p}}_h$的方差满足：
$$su{p}_{p\in \sum (\beta ,L)}Var({\hat{p}}_h(x))\le \frac{c}{n{h}^d}$$
对于某个c

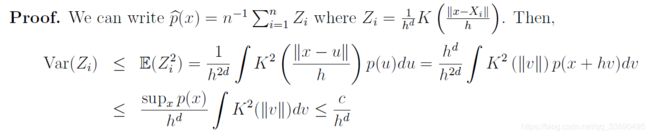
4.3 Boundary Bias

4.4 Confidence Bands and the CLT（ central-limit theorem ）

考虑一个单点$x$。令$s_n(x)=\sqrt{Var({\hat{p}}_h(x))}$。CLT（中心极限定理）意味着：
$$Z_n(x)\equiv \frac{{\hat{p}}_h(x)-p_h(x)}{s_n(x)}⇝N(0,{\tau }^2(x))$$
对于某个$\tau (x)$。即使$h=h_n$是递减的情况下也成立。特别地，假定$h_n\to 0,n{h}_n\to 0$，注意到$Z_n(x)={\sum }_{i=1}^n{L}_{ni}$，跟据Lyaponounov’s CLT，${\sum }_{i=1}^n{L}_{ni}⇝N(0,1)$只要：
$$\underset{n\to \infty }{\lim }\sum _{i=1}^n\mathbb{E}[L_{n,i}{]}^{2+\delta }=0$$
对某个$\delta$成立。但是这个并不会产生一个$p(x)$的置信区间，为了说明这件事：
$$\frac{{\hat{p}}_h(x)-p(x)}{s_n(x)}=\frac{{\hat{p}}_h(x)-p_h(x)}{s_n(x)}+\frac{p_h(x)-p(x)}{s_n(x)}=Z_n(x)+\frac{bias}{\sqrt{Var}(x)}$$
假定通过平衡偏差(bias)和方差(variance)最优化了risk，那么第二项是某个常数c，因此$$\frac{{\hat{p}}_h(x)-p(x)}{s_n(x)}⇝N(c,{\tau }^2(x))$$
这意味着一个通常的置信区间${\hat{p}}_h(x)\pm z_{\frac{\alpha }{2}}s(x)$将不会以概率$1-\alpha$盖住$p(x)$。一个对于这个问题的补救就是使估计不光滑（为什么？）（One fix for this is to undersmooth the estimator. (We sacrfice risk for coverage.)）一个更简单的想法就是只把${\hat{p}}_h(x)\pm z_{\frac{\alpha }{2}}s(x)$解释成$p_h(x)$的置信区间。
但是这个只在一点处给出了置信区间，为了得到Confidence band我们需要使用bootsrap方法。令$P_n$是$X_1,...,X_n$的经验分布，想法就是估计分布：
$$F_n(t)=\mathbb{P}(\sqrt{n{h}^d}\Vert {\hat{p}}_h(x)-p_h(x){\Vert }_{\infty }<t)$$
使用bootsrap estimator(如下)作为上面的估计
$${\hat{F}}_n(t)=\mathbb{P}((\sqrt{n{h}^d}\Vert {\hat{p}}_h^{\ast }(x)-{\hat{p}}_h(x){\Vert }_{\infty }<t|X_1,...,X_n)$$
其中${\hat{p}}_h^{\ast }$产生于bootstrap 样本$X_1^{\ast },...,X_n^{\ast }\sim P_n$
下面是算法：
1.令$P_n$是经验分布满足在每个点$X_i$放置一个质量$\frac{1}{n}$的质量块
2.从分布$P_n$中抽取$X_1^{\ast },...,X_n^{\ast }$。这成为一个bootstrap样本
3.根据boostrap样本计算对应的密度估计${\hat{p}}_h^{\ast }$
4.计算$R={\sup }_x\sqrt{n{h}^d}\Vert {\hat{p}}_h^{\ast }-{\hat{p}}_h{\Vert }_{\infty }$
5.重复2-4步骤$B$次，得到$R_1,R_2,...,R_B$
6.令$z_{\alpha }$是$R_j$的$\alpha$上分位数，因此$\frac{1}{B}{\sum }_{j=1}^{B}I(R_j>z_{\alpha })\approx \alpha$
7.令$l_n(x)={\hat{p}}_h(x)-\frac{z_{\alpha }}{\sqrt{n{h}^d}},u_n(x)={\hat{p}}_h(x)+\frac{z_{\alpha }}{n{h}^d}$

定理 7

在适当的条件下(很弱)，有：
$$\underset{n\to \infty }{\mathrm{liminf}}\mathbb{P}(l_n(x)\le p_h(x)\le u(x)forallx)\ge 1-\alpha$$
图4说明了这个性质：

如果想要得到一个置信度为p的置信带，我们需要减小偏差bias(undersmooth)。一个简单的方式就是twicing。假设$\beta =2$我们使用核估计${\hat{p}}_h$，注意到对某个$C(x)$有：
$$\begin{gathered} \mathbb{E}[{\hat{p}}_h(x)]=p(x)+C(x)h^2+o(h^2) \\ \mathbb{E}[{\hat{p}}_{2h}(x)]=p(x)+C(x)4h^2+o(h^2) \end{gathered}$$
第一个式子的偏差是$b(x)=C(x)h^2$，所以如果我们定义：
$$\hat{b}(x)=\frac{{\hat{p}}_{2h}-{\hat{p}}_h(x)}{3}$$
那么
$$\mathbb{E}[\hat{b}(x)]=b(x)$$
我们定义减去偏差的估计如下：
$${\tilde{p}}_h(x)={\hat{p}}_h(x)-\hat{b}(x)=\frac{4}{3}({\hat{p}}_h(x)-\frac{1}{4}{\hat{p}}_{2h}(x))$$
一个以${\tilde{p}}_h(x)$的置信集合将是近似有效的但是不是最优的估计。这是一个基本的矛盾存在于估计和推断之间。

5.Cross-Validation

在实际操作中我们需要一个基于数据的方法来选择窗宽(bandwidth)$h$。为了达到这个，我们需要估计estimator的风险risk，在$h$上最小化估计风险estimated risk。现在我们来叙述两种交叉验证的方法。

阅读资料：

Density Estimation 10/36-702
https://blog.csdn.net/weixin_37801695/article/details/84918980
https://blog.csdn.net/liangzuojiayi/article/details/78152180
https://blog.csdn.net/unixtch/article/details/78556499