Cs231n作业-Q1-1 K-Nearest Neighbor(kNN) exercise
Cs231n作业:Q1-1 k-Nearest Neighbor
- k近邻算法
- 原理
- 步骤
- Cs231n——Knn作业
- 训练阶段
- 测试阶段
- 交叉验证
- 小结
k近邻算法
k近邻算法是一种基本分类与回归方法。 k近邻算法的输入为实例的特征向量,对应于特征空间的点;输出为实例的类别,可以取多类。
原理
假设给定一个训练数据集,对新的输入实例,在训练数据集中找出与该实例最临近的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。
步骤
k近邻法分两个阶段:
1.训练阶段:
获取训练数据集,并进行存储。
2.测试阶段:
kNN分类器将每个测试图像与所有训练图像进行比较,计算出两者之间的距离。找出k张距离最近的训练图像。在这k张距离最近的训练图像中,选择标签类别占多数的类别,作为测试图像的类别。
3.k值的交叉验证:通过交叉验证获取k值。
Cs231n——Knn作业
训练阶段
这里的数据集用的是CIFAR-10
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
# 加载CIFAR-10数据,数据路径为:'cs231n/datasets/cifar-10-batches-py'
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# 打印训练数据和测试数据的大小
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)通过训练数据和测试数据的大小可知:每张图片像素都是32 x 32 x 3,训练集有50000张,测试集有10000张。
输出:
Training data shape: (50000, 32, 32, 3)
Training labels shape: (50000,)
Test data shape: (10000, 32, 32, 3)
Test labels shape: (10000,)
这里展示来自每个类的一些图片例子:
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
# y_train == y 返回一个和向量y_train等长的由T/F组成的矩阵
idxs = np.flatnonzero(y_train == y) # 调用函数,找出标签中y类的位置(输入一个矩阵,返回其中非零元素的位置)
idxs = np.random.choice(idxs, samples_per_class, replace=False) # 从idxs中随机抽7个不重复的位置,即对应的图片位置
for i, idx in enumerate(idxs):
# 画出第一列的图所在位置的索引值,即1、11、21、31...
plt_idx = i * num_classes + y + 1 # 索引值
plt.subplot(samples_per_class, num_classes, plt_idx) # 行数、列数、索引值
plt.imshow(X_train[idx].astype('uint8')) # 绘制图像
plt.axis('off') # 不显示坐标尺寸
if i == 0:
plt.title(cls)
plt.show()输出:

为了更有效的执行代码,从训练集中选5000张作为训练实例,测试集中选500作为测试实例:
num_training = 5000
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]将图片数据进行张量变形:
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)输出:
以X_train.shape为例:第一维大小为X_train.shape[0]即变为5000 而第二维为-1表示列不知道多少,所以根据剩下纬度进行计算,即32x32x3=3027。所以最终形状为(5000,3272)
(5000, 3072) (500, 3072)
创建一个kNN分类器实例
注意:kNN只对训练数据进行存储,不做进一步处理
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)测试阶段
现在我们用kNN分类器对测试数据进行分类。
回想一下,我们可以把这个过程分为两个步骤:
- 首先,我们必须计算所有测试示例和所有训练示例之间的距离。
- 在给定这些距离中,对于每个测试示例,我们找到与其距离最近的k个的训练示例,并标注它们的类别。
让我们从计算所有训练和测试示例之间的距离矩阵开始。例如,如果有 Ntr 训练示例和 Nte测试示例,这个阶段应该生成一个 Nte x Ntr 矩阵,其中每个元素 [i, j] 表示第i个测试样本到第j个训练样本之间的距离。
首先,打开cs231n/classifier /k_nearest_neighbor.py并实现compute_distances_two_loops函数,该函数对所有(测试、训练)示例使用一个(非常低效的)双循环,并一次计算一个测试样本到所有训练样本的距离矩阵。
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension, nor use np.linalg.norm(). #
#####################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i,j] = np.sqrt(np.sum(np.square(X[i] - self.X_train[j])))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsdists[i,j]:测试样本i到训练样本j的欧氏距离
np.square( X[i] - self.X_train[j] ):第i个测试样本 - 第j个训练样本后所得到的矩阵,再对矩阵中每个元素进行平方。(每一行所有元素代表该样本的特征,下标i表示第i个样本,X[i]即所在矩阵的行即第i个样本的所有特征)。 eg:[1, 2] - [2, 3] = [-1, -1],再进行平方(square)得:[1, 1]
np.sum( np.square( X[i] - self.X_train[j] ) ):由于axis=none,对输入数组的所有元素全部加起来。eg:np.sum([1, 1]) = 2
np.sqrt( np.sum( np.square( X[i] - self.X_train[j] ) ) ):对得到的张量进行开平方根。eg:np.sqrt(np.sum([1, 1])) = 1.4142135623730951
dists[i,j] = np.sqrt( np.sum(np.square(X[i] - self.X_train[j])) ):即为测试样本i到训练样本j的欧氏距离公式。
得到一个(500, 5000)的dists矩阵。
然后,实现predict_labels方法:
def predict_labels(self, dists, k=1):
"""
给定测试点和训练点之间的距离矩阵,预测每个测试点的类别
Inputs:
- dists: 一个(num_test, num_train)大小的numpy数组,
其中dists[i, j]表示第i个测试样本到第j个训练样本的距离
Returns:
- y: 一个(num_test,)大小的numpy数组,其中y[i]表示测试样本X[i]的预测结果.
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
#########################################################################
# TODO: #
# 利用距离矩阵求出第i个测试点的k个最近邻 #
# 使用 self.y_train 查找这些最近邻对应的类别标签 #
# 将这些类别标签存储在 closest_y 中 #
# 提示: 可尝试使用 numpy.argsort 方法. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
points = np.argsort(dists[i])[:k]
for point in points:
closest_y.append(self.y_train[point])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#########################################################################
# TODO: #
# 现在您已经找到k个最近邻的类别标签 #
# 您需要在类别标签列表closest_y中找到最常见(多)的类别标签 #
# 将此类别标签存储在y_pred[i]中。如果有票数相同的类别,则选择编号小的类别 #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
y_pred[i] = np.argmax(np.bincount(closest_y))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return y_pred
自己想的(第一部分):
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
points = np.argsort(dists[i])[:k]
for point in points:
closest_y.append(self.y_train[point])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****其中numpy.argsort():返回的是数组值从小到大的索引值。此处的索引值即为从小到大距离最近的训练样本。
np.argsort(dists[i]):返回的是距测试样本距离从小到大的索引值即训练样本。
np.argsort(dists[i])[:k]:表示取前k个,即k个最近邻的训练样本
然后通过for循环,将训练样本所对应的类别即self.y_train[point],通过closest_y.append()存储在closest_y中。
别人答案(第一部分):
#找到每一个测试图片中对应的5000张训练集图片,距离最近的前k个
closest_y = self.y_train[ np.argsort(dists[i])[:k] ]第二部分:已找到k个最近领对应的类别标签,找到其中出现最多的那个类别标签
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
y_pred[i] = np.argmax(np.bincount(closest_y))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****np.bincount(closest_y):统计closest_y中元素出现的次数。返回0-序列元素最大值的数组中,每个元素出现的次数。
np.argmax(np.bincount(closest_y)):沿给定轴返回最大的索引。即得到closest_y中出现次数最多的那个元素。(且如果有元素出现次数最多有相同的情况,则选择编号较小的那个元素)。
最后保存在y_ored[i]中,表示测试样本X[i]的预测类别(即预测结果)。
现在实现函数predict_labels并运行以下代码:
我们使用k = 1(这是最近邻1)
# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))输出:
Got 137 / 500 correct => accuracy: 0.274000
您应该期望看到比k = 1时稍微好一点的性能。当k = 5时:
y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))输出:
Got 139 / 500 correct => accuracy: 0.278000
现在让我们使用部分向量化来加速距离矩阵的计算(提升距离计算的效率),只有一个循环,实现compute_distances_one_loop函数:
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i,:] = np.sqrt(np.sum(np.square(X[i] - self.X_train[:]), axis=1))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsX[i]-self.X_train[:]:表示第i个测试样本与所有训练样本的差。
np.square(X[i] - self.X_train[:]):第i个测试样本与所有样本的差所得矩阵后再平方。
np.sum(np.square(X[i] - self.X_train[:]),axis=1):按1轴进行求和,即横向求和。 此处得到一向量:表示第i个测试样本对各个训练样本的特征值的差后在求平方和。——建议写个Demo模拟一下,就明白了TAT。
dists[i,:] =np.sqrt(np.sum(np.square(X[i] - self.X_train[:]), axis=1)),进行开根号,得到第i个测试样本到所有训练样本的欧氏距离。
在notebook中运行compute_distances_one_loop代码:
dists_one = classifier.compute_distances_one_loop(X_test)为了确保我们的向量化实现是正确的,将运行结果与前面方法的结果进行对比。对比两个矩阵是否相等的方法有很多,比较简单的一种是使用Frobenius范数。Frobenius范数表示的是两个矩阵所有元素的差值的平方和的平方根。即将两个矩阵reshape成向量后,它们之间的欧式距离。
difference = np.linalg.norm(dists - dists_one, ord='fro')
print('One loop difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')输出:
One loop difference was: 0.000000
Good! The distance matrices are the same
现在在compute_distances_no_loops中实现完全向量化的版本:(这个是真的有点儿东西…OrZ…)
想法是利用平方差公式:
( X − Y ) 2 = X 2 − 2 X Y + Y 2 . (X-Y)^2 = X^2-2XY+Y^2. (X−Y)2=X2−2XY+Y2.
使用矩阵乘法和两次广播加法,直接算出距离。
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists = np.multiply(np.dot(X,self.X_train.T),-2)
sq1 = np.sum(np.square(X),axis=1,keepdims=True)
sq2 = np.sum(np.square(self.X_train),axis=1)
dists = np.add(dists,sq1)
dists = np.add(dists,sq2)
dists = np.sqrt(dists)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists这地方我还没理解透彻,初略讲讲算了些啥:
np.multiply(np.dot(X,self.X_train.T),-2):计算出-2XY
np.sum(np.square(X),axis=1,keepdims=True):计算X2,然后以竖轴为基准 ,同行相加。通过keepdims=True保持其多维特性。
np.sum(np.square(self.X_train),axis=1):计算Y2,然后以竖轴为基准,同行相加,不保持其多维特性。
最后计算出:x2+y2-2xy,再通过开平方根,得到测试样本到训练样本的欧氏距离。
在notebook中运行compute_distances_no_loops代码:
# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
dists_two = classifier.compute_distances_no_loops(X_test)
# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('No loop difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')输出:
No loop difference was: 0.000000
Good! The distance matrices are the same
对比一下三种方法的实现速度:
使用完全向量化的实现,您应该会看到明显更快的性能!
注意:这取决于你用的是什么机器,当你从两个循环到一个循环时,你可能看不到加速,甚至可能会放缓。
# Let's compare how fast the implementations are
def time_function(f, *args):
"""
Call a function f with args and return the time (in seconds) that it took to execute.
"""
import time
tic = time.time()
f(*args)
toc = time.time()
return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)
# You should see significantly faster performance with the fully vectorized implementation!
# NOTE: depending on what machine you're using,
# you might not see a speedup when you go from two loops to one loop,
# and might even see a slow-down.输出:
果然,我的机器使我从两个循环到一个循环时,没看到加速,甚至还放缓了。。
Two loop version took 38.191042 seconds
One loop version took 82.484406 seconds
No loop version took 1.039741 seconds
交叉验证
我们实现了k近邻分类器,但是我们任意设置了k = 5。现在,我们将通过交叉验证来确定这个超参数的最佳值。
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# 将训练数据分成不同的折。分割后,训练样本和对应的样本标签 #
# 被包含在数组X_train_folds和y_train_folds中,数组长度为折数num_folds #
# 其中y_train_folds[i]是一个标签向量,表示X_train_folds[i]中所有的标签. #
# 提示: 尝试使用numpy array_split函数. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# 将不同k值下的准确率保存在一个字典中。交叉验证后,k_to_accuracies[k]保存了一个长度为折数的list,值为k值下的准确率。
k_to_accuracies = {}
################################################################################
# TODO: #
# 通过k折的交叉验证,找到最佳值k。对于每一个k值,执行kNN算法num_folds次 #
# 每一次执行中,只有一折为验证集,其他的为训练集 #
# 将不同k值在不同折上的验证结果保存在k_to_accuracies字典中 #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
classifier = KNearestNeighbor()
for i in k_choices: # 对每一个K值执行
accuracies = np.zeros(num_folds) # 保存每折对应的准确率[0. 0. 0. 0. 0.]
for fold in range(num_folds): # 执行knn算法num_folds次
temp_X = X_train_folds[:]
temp_y = y_train_folds[:]
X_validate_fold = temp_X.pop(fold)
y_validate_fold = temp_y.pop(fold)
temp_X = np.array([y for x in temp_X for y in x])
temp_y = np.array([y for x in temp_y for y in x])
classifier.train(temp_X,temp_y)
y_test_pred = classifier.predict(X_validate_fold, k=i)
num_correct = np.sum(y_test_pred == y_validate_fold)
accuracy = num_correct / num_test
accuracies[fold] = accuracy
k_to_accuracies[i] = accuracies
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))第一部分:将训练数据切分为不同的折。切分后,训练样本和对应的样本标签被包含在X_train_folds和y_train_folds之中。
np.array_split(X_train, num_folds):将X_train分为num_folds折。
np.array_split(y_train, num_folds):将y_train分为num_folds折。
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS y_train_folds[i]得到的是一个向量,表示对应i折中的向量,即X_train_folds[i]中所有样本的标签。
第二部分:通过k折的交叉验证找出最佳k值。
对于每一个k值,均要执行kNN算法num_folds次,每一次执行,选择一折为验证集,其他的为训练集。最后将不同k值下不同折上的验证结果保存在k_to_accuracies字典中。
① 因为要对每一个k值进行算法,所以第一层循环即为foriin k_choices,在k_choices中选择每一个k值。
② 又因为对每一个k值,均要执行kNN算法num_folds次,所以第二层循环即为forfoldin range(num_folds),表示执行num_fold次。
③ 复制所有折中的所有数据:temp_X = X_train_folds[:]和temp_y = y_train_folds[:]
④ 取当前次数fold的折为验证集,即X_validate_fold = temp_X.pop(fold)和y_validate_fold = temp_y.pop(fold)
⑤ 此时,所剩下的折数即为训练集,要所有剩下折的数据,合并为一折作为训练集。即temp_X = np.array([y for x in temp_X for y in x])和temp_y = np.array([y for x in temp_y for y in x])即( temp_X为多折数据,先通过for x in temp_X 获取对应的折, 再通过 y for y in x 将每个折的数据,依次合并为一折)
⑥ 最后通过kNN分类器进行预测:
: 先进行classifier.train(temp_X,temp_y)进行数据存储
: 再传入验证集X_validate_fold以及此时的k值i。即是y_test_pred = classifier.predict(X_validate_fold, k=i)进行预测。
: 计算出预测的正确数量:np.sum(y_test_pred == y_validate_fold)
: 算出精确率:accuracy = num_coorect / num_test
: 存入accuracies[fold]中,表示不同折上的精确率accuracies[fold] = accuracy
⑦ 然后存储到k_to_accuracies[i]中,表示不同k值在不同折上的精确率。k_to_accuracies[i] = accuracies
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
classifier = KNearestNeighbor()
for i in k_choices: # 对每一个K值执行
accuracies = np.zeros(num_folds) # 保存每折对应的准确率[0. 0. 0. 0. 0.]
for fold in range(num_folds): # 执行knn算法num_folds次
temp_X = X_train_folds[:]
temp_y = y_train_folds[:]
X_validate_fold = temp_X.pop(fold)
y_validate_fold = temp_y.pop(fold)
temp_X = np.array([y for x in temp_X for y in x])
temp_y = np.array([y for x in temp_y for y in x])
classifier.train(temp_X,temp_y)
y_test_pred = classifier.predict(X_validate_fold, k=i)
num_correct = np.sum(y_test_pred == y_validate_fold)
accuracy = num_correct / num_test
accuracies[fold] = accuracy
k_to_accuracies[i] = accuracies
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****输出准确率:
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))输出:
k = 1, accuracy = 0.526000
k = 1, accuracy = 0.514000
k = 1, accuracy = 0.528000
k = 1, accuracy = 0.556000
k = 1, accuracy = 0.532000
k = 3, accuracy = 0.478000
k = 3, accuracy = 0.498000
k = 3, accuracy = 0.480000
k = 3, accuracy = 0.532000
k = 3, accuracy = 0.508000
k = 5, accuracy = 0.496000
k = 5, accuracy = 0.532000
k = 5, accuracy = 0.560000
k = 5, accuracy = 0.584000
k = 5, accuracy = 0.560000
k = 8, accuracy = 0.524000
k = 8, accuracy = 0.564000
k = 8, accuracy = 0.546000
k = 8, accuracy = 0.580000
k = 8, accuracy = 0.546000
k = 10, accuracy = 0.530000
k = 10, accuracy = 0.592000
k = 10, accuracy = 0.552000
k = 10, accuracy = 0.568000
k = 10, accuracy = 0.560000
k = 12, accuracy = 0.520000
k = 12, accuracy = 0.590000
k = 12, accuracy = 0.558000
k = 12, accuracy = 0.566000
k = 12, accuracy = 0.560000
k = 15, accuracy = 0.504000
k = 15, accuracy = 0.578000
k = 15, accuracy = 0.556000
k = 15, accuracy = 0.564000
k = 15, accuracy = 0.548000
k = 20, accuracy = 0.540000
k = 20, accuracy = 0.558000
k = 20, accuracy = 0.558000
k = 20, accuracy = 0.564000
k = 20, accuracy = 0.570000
k = 50, accuracy = 0.542000
k = 50, accuracy = 0.576000
k = 50, accuracy = 0.556000
k = 50, accuracy = 0.538000
k = 50, accuracy = 0.532000
k = 100, accuracy = 0.512000
k = 100, accuracy = 0.540000
k = 100, accuracy = 0.526000
k = 100, accuracy = 0.512000
k = 100, accuracy = 0.526000
画图进行展示:
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()输出:
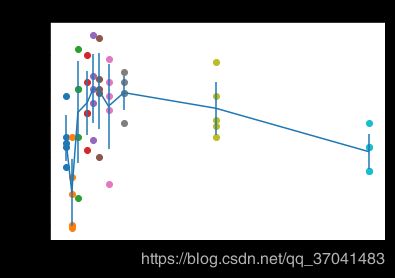
根据交叉验证的结果,知道k=10时,为最优的k,然后在全量数据上进行实验,将得到超过28%的准确率。
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))输出:
Got 141 / 500 correct => accuracy: 0.282000
小结
- 这第一个kNN的作业,感觉吃力TAT,特别在完全向量化的操作上(有点儿东西…)
- 尽量使用向量化进行计算,能提高计算效率
- 再接再厉…
