统计学-贾俊平(第四版)学习笔记
目录
- 5. 概率与概率分布
- 5.1 概率的定义
- 5.2 全概率&贝叶斯
- 5.3 离散随机变量&概率函数
- 5.4 连续随机变量&概率密度函数
- 6. 统计量及抽样分布
- 6.1 统计量(矩、偏度、峰度)
- 6.2 由正态分布导出的几个重要分布( χ 2 \chi^2 χ2,t分布,F分布)
- 6.3 样本均值分布&中心极限定理
- 6.4 样本比例的抽样分布
- 6.5 两个样本平均值之差的分布
- 6.6 样本方差的分布
- 6.7 F分布、t分布、正态分布与卡方分布的联系与区别
- 7. 参数估计
- 7.1 参数估计的基本原理
- 7.2 一个总体参数的区间估计
- 7.3 两个总体参数的区间估计
- 7.4 样本量的确定
- 8 假设检验
- 8.1 假设检验的基本问题
- 8.2 一个总体参数的检验
5. 概率与概率分布
5.1 概率的定义
(1) 概率的古典定义
如果某一随机试验的结果有限,而且各个结果出现的可能性相等,则某一事件A发生的概率为该事件所包含的基本事件个数m与样本空间所包含的基本事件个数n的比值: P ( A ) = m n P(A)=\frac{m}{n} P(A)=nm
古典概率的局限: 随机试验只有有限个可能结果范围。
(2) 概率的统计定义
相同条件下随机试验n次,某事件A出现m次( m ≤ n m\leq n m≤n), P ( A ) = m n P(A)=\frac{m}{n} P(A)=nm,随着n增大,波动幅度减小,趋于稳定,该稳定之为A事件的概率。
概率统计定义局限:要求大量重复实验
(3) 主观概率的定义
概率是一个决策者根据个人对某个事件是否发生以及本人掌握的信息对该事件发生可能性的判断。
5.2 全概率&贝叶斯
互斥事件: P ( A U B ) = P ( A ) + P ( B ) P(AUB)=P(A)+P(B) P(AUB)=P(A)+P(B)
独立事件: P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
互斥事件一定是相互依赖(不独立)的,但相互依赖的事件不一定是互斥的
全概率公式:某一事件B的发生各种可能的原因 A i ( i = 1 , 2 , . . . , n ) A_i(i=1,2,...,n) Ai(i=1,2,...,n),如果B是由原因 A i A_i Ai所引起的,则B发生的概率是 P ( A i B ) ( i = 1 , 2 , . . . , n ) P(A_iB)(i=1,2,...,n) P(AiB)(i=1,2,...,n)。每一 A i A_i Ai发生都可能导致B发生的相应概率是 P ( B ∣ A i ) P(B|A_i) P(B∣Ai)
P ( B ) = ∑ i = 1 n P ( A i B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) P(B)=\sum_{i=1}^{n}P(A_iB)=\sum_{i=1}^{n}P(A_i)P(B|A_i) P(B)=i=1∑nP(AiB)=i=1∑nP(Ai)P(B∣Ai)
贝叶斯公式:在条件概率的基础上寻找事件发生的原因
P ( A i ∣ B ) = P ( A i ) P ( B ∣ A i ) ∑ i = j n P ( A j ) P ( B ∣ A j ) P(A_i|B)=\frac{P(A_i)P(B|A_i)}{\sum_{i=j}^{n}P(A_j)P(B|A_j)} P(Ai∣B)=∑i=jnP(Aj)P(B∣Aj)P(Ai)P(B∣Ai)
观察到事件P(B),学着导致A发生的每个原因的概率 P ( A i ) P(A_i) P(Ai)。 P ( A i ) P(A_i) P(Ai)先验概率, P ( A i ∣ B ) P(A_i|B) P(Ai∣B)后验概率。后验概率是先验概率经过观测结果加以修正的概率。
5.3 离散随机变量&概率函数
X的所有可能值具有确定概率 P ( x 1 ) , P ( x 2 ) , . . . , P ( x n ) P(x_1),P(x_2),...,P(x_n) P(x1),P(x2),...,P(xn),其中 P ( x i ) = P ( X = x i ) P(x_i)=P(X=x_i) P(xi)=P(X=xi)成为概率函数,则X成为P(X)的随机变量,P(X)成为随机变量X的概率函数。
(1)期望值( E ( X ) E(X) E(X)或 μ \mu μ):在离散型随机变量X的一切可能值得完备组中,各可能值 x i x_i xi与其对应概率 p i p_i pi得乘积之和。表示平均水平/集中程度。
(2)方差( σ 2 \sigma^2 σ2或 D ( X ) D(X) D(X)):每一个随机变量取值与期望值的离差平方之期望值。 σ 2 = D ( X ) = E [ X − E ( X ) ] 2 = E ( X 2 ) − [ E ( X ) ] 2 \sigma^2=D(X)=E[X-E(X)]^2=E(X^2)-[E(X)]^2 σ2=D(X)=E[X−E(X)]2=E(X2)−[E(X)]2用来反映随机变量的离散程度。
(3)标准差( σ \sigma σ):方差的平方根
(4) 离散系数 : V = σ E ( X ) :V=\frac{\sigma}{E(X)} :V=E(X)σ
0-1分布:离散随机变量X只可能取0和1两个值,其概率分布为:
P ( X = 1 ) = p P(X=1)=p P(X=1)=p
P ( X = 0 ) = 1 − p = q P(X=0)=1-p=q P(X=0)=1−p=q
或 P ( x ) = p x q 1 − x , x = 0 , 1 P(x)=p^xq^{1-x}, x=0,1 P(x)=pxq1−x,x=0,1
均匀分布: P ( X = x i ) = p P(X=x_i)=p P(X=xi)=p 对于所有可能取值
二项分布:包含n个相同的试验,每次试验只有两个可能的结果A,B。出现A的概率 p p p每一次试验是相同的。出现B的概率 q q q且 p + q = 1 p+q=1 p+q=1;试验相互独立;试验A/B可以计数,即实验结果对应一个离散随机变量。这种随机变量服从的概率分布为二项分布。具有上诉特征的n次重复独立试验为贝努里试验。
P ( X = x ) = C n x p x q n − x , x = 0 , 1 , 2 , . . , n P(X=x)=C_n^xp^xq^{n-x}, x=0,1,2,..,n P(X=x)=Cnxpxqn−x,x=0,1,2,..,n
随机变量X服从二项分布,参数为 n , p n,p n,p,记作 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p)
C n x = n ! x ! ( n − x ) ! C_n^x=\frac{n!}{x!(n-x)!} Cnx=x!(n−x)!n!
二项分布的期望值和方差分别为: E ( X ) = n p , D ( X ) = n p q E(X)=np, D(X)=npq E(X)=np,D(X)=npq
泊松分布:描述在一指定时间范围内或在指定的面积或提及之内某一事件出现的次数的分布。
P ( X ) = λ x e − λ x ! , x = 0 , 1 , 2 , . . . P(X)=\frac{\lambda^xe^{-\lambda}}{x!}, x=0,1,2,... P(X)=x!λxe−λ,x=0,1,2,...
λ \lambda λ为给定的时间间隔内事件的平均数。
泊松分布的期望值和方差分别为: E ( X ) = λ , D ( X ) = λ E(X)=\lambda, D(X)=\lambda E(X)=λ,D(X)=λ
例子:某企业每月发生的事故的次数;单位之间到柜台的顾客人数。
实际应用中, p ≤ 0.25 , n > 20 , n p ≤ 5 p\leq0.25,n>20,np\leq 5 p≤0.25,n>20,np≤5,p很小,n大时,泊松分布近似二项分布
5.4 连续随机变量&概率密度函数
概率密度函数:用函数 f ( x ) f(x) f(x)来表示连续型随机变量
分布函数定义为:
F ( x ) = P ( X ≤ x ) = ∫ − ∞ x f ( t ) d t F(x) = P(X\leq x) = \int_{-\infty}^x f(t)dt F(x)=P(X≤x)=∫−∞xf(t)dt
连续型随机变量的期望值月方差:
E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x = μ E(X)=\int_{-\infty}^{+\infty}xf(x)dx=\mu E(X)=∫−∞+∞xf(x)dx=μ
D ( X ) = ∫ − ∞ + ∞ [ x − E ( x ) ] 2 d x = σ 2 D(X)=\int_{-\infty}^{+\infty}[x-E(x)]^2dx = \sigma ^2 D(X)=∫−∞+∞[x−E(x)]2dx=σ2
正态分布
连续型随机变量中,最重要的一种随机变量是具有钟形概率分布的随机变量。
特别差的和特别好的都在少数,多数处在中间。
概率密度为:
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma ^2}} f(x)=σ2π1e−2σ2(x−μ)2
记作 X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma ^2) X∼N(μ,σ2)
标准正态分布, μ = 0 , σ = 1 \mu=0,\sigma=1 μ=0,σ=1
任何一个一般的正太分布可以通过线性变换转化为标准正态分布。 Z = X − μ σ ∼ N ( 0 , 1 ) Z=\frac{X-\mu}{\sigma}\sim N(0,1) Z=σX−μ∼N(0,1)
ϕ ( − x ) = 1 − ϕ ( x ) = 1 − P ( X ≤ x ) = 1 − ∫ − ∞ x 1 2 π e − t 2 2 d t \phi(-x)=1-\phi(x)=1-P(X\leq x)=1-\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt ϕ(−x)=1−ϕ(x)=1−P(X≤x)=1−∫−∞x2π1e−2t2dt
一般设 X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma^2) X∼N(μ,σ2)
P ( a ≤ X ≤ b ) = ϕ ( b − μ σ ) − ϕ ( a − μ σ ) P(a\leq X\leq b)=\phi(\frac{b-\mu}{\sigma})-\phi(\frac{a-\mu}{\sigma}) P(a≤X≤b)=ϕ(σb−μ)−ϕ(σa−μ)
3 σ \sigma σ准则
P ( ∣ X − μ ∣ ≤ 3 σ ) = 0.9973 P(|X-\mu|\leq3\sigma)=0.9973 P(∣X−μ∣≤3σ)=0.9973,可以认为X的值几乎一定落在 ( μ − 3 σ , μ + 3 σ ) (\mu-3\sigma,\mu+3\sigma) (μ−3σ,μ+3σ)内. 超过这个范围被认为异常值.
二项分布的正太分布近似
设随机变量 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p),对任意x, lim n − > ∞ P ( X − n p n p ( 1 − p ) ≤ x ) = ∫ − ∞ x 1 2 π e − t 2 2 d t \lim_{n->\infty}P(\frac{X-np}{\sqrt{np(1-p)}}\leq x)=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt limn−>∞P(np(1−p)X−np≤x)=∫−∞x2π1e−2t2dt
对于二项随机变量X,n很大,p是定值, X − n p n p ( 1 − p ) \frac{X-np}{\sqrt{np(1-p)}} np(1−p)X−np近似标准正态分布。
6. 统计量及抽样分布
6.1 统计量(矩、偏度、峰度)
统计量:从总体X中抽取一个容量为n的样本,如果由此样本构造一个函数 T ( X 1 , . . , X n ) T(X_1,..,X_n) T(X1,..,Xn),不依赖于任何未知参数,则称函数 T ( X 1 , . . , X n ) T(X_1,..,X_n) T(X1,..,Xn)是一个统计量。
概率论把数学期望及方差等概念用“矩”的概念来描述。经验分布函数 F n ( X ) F_n(X) Fn(X)的各阶矩反映了总体各阶矩的信息。
m k = 1 n ∑ i = 1 n X i k m_k=\frac{1}{n}\sum_{i=1}^nX_i^k mk=n1∑i=1nXik成为样本k阶矩。
v k = 1 n ∑ i = 1 n ( X i − X ˉ ) k v_k=\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^k vk=n1∑i=1n(Xi−Xˉ)k成为样本k阶中心矩。
α 3 = n ∑ i = 1 n ( X i − X ˉ ) 3 [ ∑ i = 1 n ( X i − X ˉ ) 2 ] 3 / 2 \alpha_3=\frac{\sqrt{n}\sum_{i=1}^n(X_i-\bar{X})^3}{[\sum_{i=1}^n(X_i-\bar{X})^2]^{3/2}} α3=[∑i=1n(Xi−Xˉ)2]3/2n∑i=1n(Xi−Xˉ)3为样本偏度。偏度反映了随机变量密度函数曲线在众数两边的对称偏斜性。如果 X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma^2) X∼N(μ,σ2), α 3 = 0 \alpha_3=0 α3=0
α 4 = n ∑ i = 1 n ( X i − X ˉ ) 4 [ ∑ i = 1 n ( X i − X ˉ ) 2 ] 2 − 3 \alpha_4=\frac{n\sum_{i=1}^n(X_i-\bar{X})^4}{[\sum_{i=1}^n(X_i-\bar{X})^2]^{2}}-3 α4=[∑i=1n(Xi−Xˉ)2]2n∑i=1n(Xi−Xˉ)4−3为样本峰度。峰度反映了密度函数曲线在众数附近“峰”的尖峭程度。如果 X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma^2) X∼N(μ,σ2), α 4 = 0 \alpha_4=0 α4=0
6.2 由正态分布导出的几个重要分布( χ 2 \chi^2 χ2,t分布,F分布)
由正态分布导出的几个重要分布:
-
χ 2 \chi^2 χ2分布(卡方分布)
设随机变量 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn相互独立,且 X i X_i Xi服从标准正态分布N(0,1),则它们的平方和 ∑ i = 1 n χ i 2 \sum_{i=1}^n\chi_i^2 ∑i=1nχi2服从自由度为n的 χ 2 \chi^2 χ2分布。
自由度:独立变量的个数,或二次型的秩。例如, Y = x 2 Y=x^2 Y=x2是自由度为1的 χ 2 \chi^2 χ2分布,rank(Y)=1。
E ( χ 2 ) = n E(\chi^2)=n E(χ2)=n, D ( χ 2 ) = 2 n D(\chi^2)=2n D(χ2)=2n
可加性, χ 1 2 ∼ χ 2 ( n 1 ) \chi_1^2\sim \chi^2(n_1) χ12∼χ2(n1), χ 2 2 ∼ χ 2 ( n 2 ) \chi_2^2\sim \chi^2(n_2) χ22∼χ2(n2) 独立: χ 1 2 + χ 2 2 ∼ χ 2 ( n 1 + n 2 ) \chi_1^2+\chi_2^2\sim \chi^2(n_1+n_2) χ12+χ22∼χ2(n1+n2)

自由度足够大,概率密度曲线趋于对称, n → + ∞ n\rightarrow + \infty n→+∞, χ 2 \chi^2 χ2的极限分布是正态分布。 -
t分布
设随机变量 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X\sim N(0,1),Y\sim \chi^2(n) X∼N(0,1),Y∼χ2(n),且X与Y独立,则 t = X Y / n t=\frac{X}{\sqrt{Y/n}} t=Y/nX,其分布称为t分布,记为t(n)

当 n ≥ 2 , E ( t ) = 0 n\geq2,E(t)=0 n≥2,E(t)=0
当 n ≥ 3 , D ( t ) = n n − 2 n\geq3,D(t)=\frac{n}{n-2} n≥3,D(t)=n−2n
t(n)密度函数的两侧都按t-(n+1)的速度趋向于0.
自由度为1的分布称为柯西分布。自由度n增加t分布的密度函数越接近标准正态分布的密度函数。实际应用中 n ≥ 30 n\geq30 n≥30 t分布和标准正态分布非常接近。
与t分布有关的抽样分布:
X 1 , . . , X n X_1,..,X_n X1,..,Xn正态分布 N ∼ ( μ , σ 2 ) N\sim (\mu,\sigma^2) N∼(μ,σ2), X ˉ = 1 n ∑ i = 1 n X i \bar{X}=\frac{1}{n}\sum_{i=1}^nX_i Xˉ=n1∑i=1nXi, S 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 S^2=\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2 S2=n1∑i=1n(Xi−Xˉ)2
n ( X ˉ − μ ) S ∼ t ( n − 1 ) \frac{\sqrt{n}(\bar{X}-\mu)}{S}\sim t(n-1) Sn(Xˉ−μ)∼t(n−1)
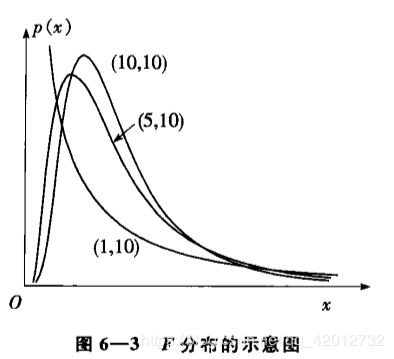
3.F分布
定义随机变量Y和Z相互独立,且Y和Z服从自由度为m和n的 χ 2 \chi^2 χ2分布,则随机变量X
X = Y / m Z / n = n Y m Z X=\frac{Y/m}{Z/n}=\frac{nY}{mZ} X=Z/nY/m=mZnY
则X服从第一自由度为m,第二自由度为n的F分布,记为F(m,n)。
E ( X ) = n n − 2 , n > 2 E(X)=\frac{n}{n-2}, n>2 E(X)=n−2n,n>2
D ( X ) = 2 n 2 ( m + n − 2 ) m ( n − 2 ) ( n − 4 ) , n > 4 D(X)=\frac{2n^2(m+n-2)}{m(n-2)(n-4)}, n>4 D(X)=m(n−2)(n−4)2n2(m+n−2),n>4
如果随机变量X服从t(n)分布,则 X 2 X^2 X2服从F(1,n)的F分布。
6.3 样本均值分布&中心极限定理
样本均值的分布
当总体分布为正态分布 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)时, X ˉ \bar{X} Xˉ的抽样分布仍为正太分布, E ( X ˉ ) = μ E(\bar{X})=\mu E(Xˉ)=μ, D ( X ˉ ) = σ 2 n D(\bar{X})=\frac{\sigma^2}{n} D(Xˉ)=nσ2,则 X ˉ ∼ N ( μ , σ 2 n ) \bar{X} \sim N(\mu,\frac{\sigma^2}{n}) Xˉ∼N(μ,nσ2)
X ˉ \bar{X} Xˉ的期望值与总体均值相同,方差为总体方差的1/n。
中心极限定理
设从均值为 μ \mu μ、方差为 σ 2 \sigma^2 σ2(有限)的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值 X ˉ \bar{X} Xˉ的抽样分布近似服从均值为 μ \mu μ,方差为 σ 2 / n \sigma^2 /n σ2/n的正态分布。
充分大:与总体分布形状有关。总体偏离正态越远,则要求n越大。实际应用中要求 n ≥ 30 n\geq30 n≥30。
大样本小样本
并不以样本容量大小来区分。
小样本问题: 在样本容量固定的条件下进行的统计推断、问题分析,不管样本容量多大,都称为小样本问题。
大样本问题: 在样本容量 n → ∞ n\rightarrow \infty n→∞的条件下进行的统计推断、问题分析则称为大样本问题。
一般统计学中 n ≥ 30 n\geq30 n≥30为大样本,n<30为小样本只是一种经验说法。
6.4 样本比例的抽样分布
抽样比例: p ^ = X n \hat{p}=\frac{X}{n} p^=nX
总体比例: π \pi π
由二项分布的原理和渐近分布的理论可知,n充分大时, p ^ \hat{p} p^的分布可用正态分布逼近。
p ^ ∼ N ( π , π ( 1 − π ) n ) \hat{p}\sim N(\pi,\frac{\pi(1-\pi)}{n}) p^∼N(π,nπ(1−π))
6.5 两个样本平均值之差的分布
X 1 ˉ \bar{X_1} X1ˉ是独立地抽自总体 X 1 ∼ N ( μ 1 , σ 1 2 ) X_1 \sim N(\mu_1,\sigma^2_1) X1∼N(μ1,σ12)的一个容量为 n 1 n_1 n1的样本的均值。
X 2 ˉ \bar{X_2} X2ˉ是独立地抽自总体 X 2 ∼ N ( μ 2 , σ 2 2 ) X_2 \sim N(\mu_2,\sigma^2_2) X2∼N(μ2,σ22)的一个容量为 n 2 n_2 n2的样本的均值。
E ( X 1 ˉ − X 2 ˉ ) = E ( X 1 ˉ ) − E ( X 2 ˉ ) = μ 1 − μ 2 E(\bar{X_1}-\bar{X_2})=E(\bar{X_1})-E(\bar{X_2})=\mu_1-\mu_2 E(X1ˉ−X2ˉ)=E(X1ˉ)−E(X2ˉ)=μ1−μ2
D ( X 1 ˉ − X 2 ˉ ) = D ( X 1 ˉ ) + E ( X 2 ˉ ) = σ 1 2 n 1 + σ 2 2 n 2 D(\bar{X_1}-\bar{X_2})=D(\bar{X_1})+E(\bar{X_2})=\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2} D(X1ˉ−X2ˉ)=D(X1ˉ)+E(X2ˉ)=n1σ12+n2σ22
- 如果两个总体均为正态分布,则 X 1 ˉ − X 2 ˉ \bar{X_1}-\bar{X_2} X1ˉ−X2ˉ也为正态分布
- 若 n 1 ≥ 30 , n 2 ≥ 30 n_1\geq 30,n_2\geq 30 n1≥30,n2≥30,则 X 1 ˉ − X 2 ˉ \bar{X_1}-\bar{X_2} X1ˉ−X2ˉ为正态分布,不管总体分布如何。
6.6 样本方差的分布
样本方差的分布:
设总体分布为 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)的正太分布,则样本方差 S 2 S^2 S2的分布为:
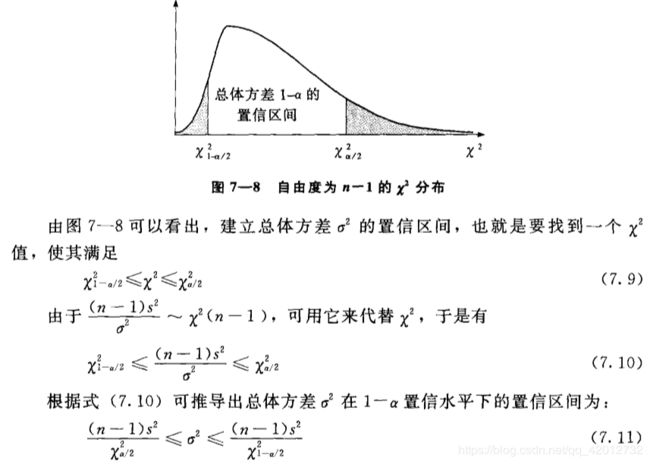
( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1) σ2(n−1)S2∼χ2(n−1)
两个样本方差比的分布:
设 X 1 , . . . , X n 1 X_1,...,X_{n_1} X1,...,Xn1总体分布为 N ( μ 1 , σ 1 2 ) N(\mu_1,\sigma_1^2) N(μ1,σ12)的正太分布的一个样本。设 Y 1 , . . . , Y n 2 Y_1,...,Y_{n_2} Y1,...,Yn2总体分布为 N ( μ 2 , σ 2 2 ) N(\mu_2,\sigma_2^2) N(μ2,σ22)的正太分布的一个样本。相互独立
S x 2 / S y 2 σ 1 2 / σ 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) \frac{S_x^2/S_y^2}{\sigma^2_1/\sigma^2_2}\sim F(n_1-1,n_2-1) σ12/σ22Sx2/Sy2∼F(n1−1,n2−1)
其中, S x 2 = 1 n 1 − 1 ∑ i = 1 n 1 ( X i − X ˉ ) 2 S_x^2=\frac{1}{n_1-1}\sum_{i=1}^{n_1}(X_i-\bar{X})^2 Sx2=n1−11i=1∑n1(Xi−Xˉ)2
6.7 F分布、t分布、正态分布与卡方分布的联系与区别
- t分布vs正态分布:t分布与正态分布相比多了自由度参数,在小样本中,能更好的剔除异常值对于小样本的影响,从而能够准确地抓住数据的集中趋势和离散趋势。
- 卡方分布vs正态分布 :卡方分布是k个服从正态分布的随机变量的平方和所服从的分布。其参数只有一个——自由度,当自由度很大时, χ 2 \chi^2 χ2近似服从正态分布。
- F分布是两个服从卡方分布的随机变量各自除以它们的自由度的商。
- 正态分布是以上所有分布的基础。
7. 参数估计
7.1 参数估计的基本原理
参数估计:用样本统计量去估计总体的参数。
在参数古籍中,用来估计总体参数的统计量的名称称为估计量 θ ^ \hat{\theta} θ^。
根据一个具体的样本计算出来的估计量的数值称为估计值。
点估计:用样本统计量 θ ^ \hat{\theta} θ^的某个取值直接作为总体参数 θ \theta θ的估计值。
区间估计:在点估计的基础上,给出总体参数估计的一个区间范围,该区间通常由样本统计量加减估计误差得到。
约有95%的样本均值会落在 μ \mu μ的两个标准差的范围内=约有95%的样本均值所构造的两个标准差的区间回包括 μ \mu μ
置信区间:由样本统计量所构造的总体的参数的估计区间。
置信水平:置信区间中包含总体参数真值的次数所占的比例。
100个样本构造的总体参数的100个置信区间,由95%的区间包含了总体参数的真值。

评估估计量的标准:
- 无偏性:指估计量抽样分布的数学期望等于被估计的总体参数。 E ( θ ^ ) = θ E(\hat{\theta})=\theta E(θ^)=θ,则称 θ ^ \hat{\theta} θ^为 θ \theta θ的无偏估计量。
- 有效性:对同一总体参数的两个无偏估计量,由更小标准差的估计量更有效。
- 一致性:随着样本量的增大,点估计量的值越来越接近被估计总体的参数。
7.2 一个总体参数的区间估计
如何用样本统计量来构造一个总体参数的置信区间?
总体均值的区间估计
-
条件:(正态总体、方差已知)/(非正态总体、大样本)
分布:样本均值 x ˉ \bar{x} xˉ的抽样分布服从 N ( μ , σ 2 / n ) N(\mu,\sigma^2/n) N(μ,σ2/n)
置信区间:在 1 − α 1-\alpha 1−α置信水平下的置信区间: x ˉ ± z α / 2 σ n \bar{x} \pm z_{\alpha/2}\frac{\sigma}{\sqrt{n}} xˉ±zα/2nσ
其中 z α / 2 z_{\alpha/2} zα/2为标准正态分布上右侧面积为 α / 2 \alpha/2 α/2时的z值, z α / 2 σ n z_{\alpha/2}\frac{\sigma}{\sqrt{n}} zα/2nσ是估计误差。
若 σ 2 \sigma^2 σ2未知,只要是在大样本条件下,可以用样本方差 s 2 s^2 s2代替。 -
条件:正态总体、方差未知、小样本
分布:样本均值经过标准化后的随机变量服从自由度为n-1的t分布, x ˉ − μ s / n ∼ t ( n − 1 ) \frac{\bar{x}-\mu}{s/\sqrt{n}}\sim t(n-1) s/nxˉ−μ∼t(n−1)
置信区间:在 1 − α 1-\alpha 1−α置信水平下的置信区间: x ˉ ± t α / 2 s n \bar{x} \pm t_{\alpha/2}\frac{s}{\sqrt{n}} xˉ±tα/2ns
其中 t α / 2 t_{\alpha/2} tα/2是自由度为n-1,t分布上右侧面积为 α / 2 \alpha/2 α/2时的t值

总体比例的区间估计
样本比例p,总体比例 π \pi π,样本足够大时,服从正态分布。 E ( p ) = π , σ p 2 = π ( 1 − π ) n E(p)=\pi, \sigma_p^2=\frac{\pi(1-\pi)}{n} E(p)=π,σp2=nπ(1−π)
1 − α 1-\alpha 1−α置信水平下的置信区间: p ± z α / 2 π ( 1 − π ) n p\pm z_{\alpha/2}\sqrt{\frac{\pi(1-\pi)}{n}} p±zα/2nπ(1−π)
因为 π \pi π未知,用p代替: p ± z α / 2 p ( 1 − p ) n p\pm z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}} p±zα/2np(1−p)
总体方差的区间估计
抽样方差服从自由度为n-1的 χ 2 \chi^2 χ2分布
总结:
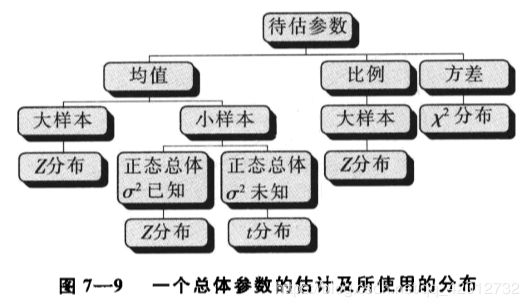
Z分布就是正态分布。
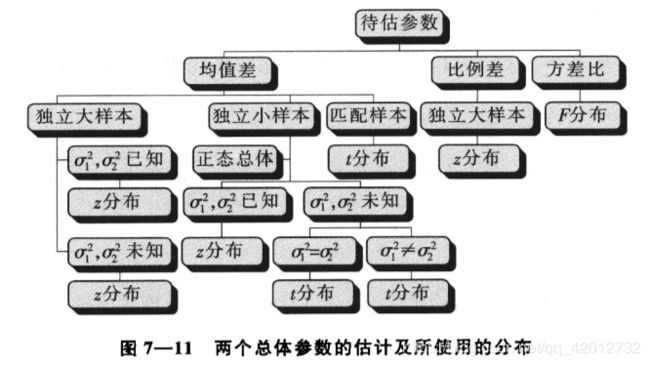
7.3 两个总体参数的区间估计
两个总体均值之差的区间估计
(1) 独立样本,大样本:
( x 1 ˉ − x 2 ˉ ) (\bar{x_1}-\bar{x_2}) (x1ˉ−x2ˉ)服从正态分布,
E ( x 1 ˉ − x 2 ˉ ) = μ 1 − μ 2 E(\bar{x_1}-\bar{x_2})=\mu_1-\mu_2 E(x1ˉ−x2ˉ)=μ1−μ2, D ( x 1 ˉ − x 2 ˉ ) = σ 1 2 n 1 + σ 2 2 n 2 D(\bar{x_1}-\bar{x_2})=\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2} D(x1ˉ−x2ˉ)=n1σ12+n2σ22
置信区间: ( x 1 ˉ − x 2 ˉ ) ± z α / 2 σ 1 2 n 1 + σ 2 2 n 2 (\bar{x_1}-\bar{x_2})\pm z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}} (x1ˉ−x2ˉ)±zα/2n1σ12+n2σ22
当总体方差未知时,样本方差替代: ( x 1 ˉ − x 2 ˉ ) ± z α / 2 s 1 2 n 1 + s 2 2 n 2 (\bar{x_1}-\bar{x_2})\pm z_{\alpha/2}\sqrt{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}} (x1ˉ−x2ˉ)±zα/2n1s12+n2s22
(2) 正态分布,独立样本,小样本:
总体方差已知: ( x 1 ˉ − x 2 ˉ ) ± z α / 2 σ 1 2 n 1 + σ 2 2 n 2 (\bar{x_1}-\bar{x_2})\pm z_{\alpha/2}\sqrt{\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}} (x1ˉ−x2ˉ)±zα/2n1σ12+n2σ22
总体方差未知但相等:总体方差的合并估计量 s p 2 = ( n 1 − 1 ) s 1 2 + ( n 2 − 1 ) s 2 2 n 1 + n 2 − 2 s_p^2=\frac{(n_1-1)s^2_1+(n_2-1)s_2^2}{n_1+n_2-2} sp2=n1+n2−2(n1−1)s12+(n2−1)s22,
服从t分布, ( x 1 ˉ − x 2 ˉ ) − ( μ 1 − μ 2 ) s p 1 n 1 + 1 n 2 ∼ t ( n 1 + n 2 − 2 ) \frac{(\bar{x_1}-\bar{x_2})-(\mu_1-\mu_2)}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\sim t(n_1+n_2-2) spn11+n21(x1ˉ−x2ˉ)−(μ1−μ2)∼t(n1+n2−2),
置信区间 ( x 1 ˉ − x 2 ˉ ) ± t α / 2 ( n 1 + n 2 − 2 ) s p 2 n 1 + s p 2 n 2 (\bar{x_1}-\bar{x_2})\pm t_{\alpha/2}(n_1+n_2-2)\sqrt{\frac{s^2_p}{n_1}+\frac{s^2_p}{n_2}} (x1ˉ−x2ˉ)±tα/2(n1+n2−2)n1sp2+n2sp2
总体方差未知且不相等: ( x 1 ˉ − x 2 ˉ ) (\bar{x_1}-\bar{x_2}) (x1ˉ−x2ˉ)经标准化后服从自由度为v的t分布,
自由度v, v = ( s 1 2 n 1 + s 2 2 n 2 ) 2 ( s 1 2 / n 1 ) 2 n 1 − 1 + ( s 2 2 / n 2 ) 2 n 2 − 1 v=\frac{(\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2})^2}{\frac{(s^2_1/n_1)^2}{n_1-1}+\frac{(s^2_2/n_2)^2}{n_2-1}} v=n1−1(s12/n1)2+n2−1(s22/n2)2(n1s12+n2s22)2
两个总体比例之差的区间估计
正态分布
E ( p 1 ˉ − p 2 ˉ ) = π 1 − π 2 E(\bar{p_1}-\bar{p_2})=\pi_1-\pi_2 E(p1ˉ−p2ˉ)=π1−π2, D ( p 1 ˉ − p 2 ˉ ) = π 1 ( 1 − π 1 ) n 1 + π 2 ( 1 − π 2 ) n 2 D(\bar{p_1}-\bar{p_2})=\frac{\pi_1(1-\pi_1)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2} D(p1ˉ−p2ˉ)=n1π1(1−π1)+n2π2(1−π2)
置信区间: ( p 1 − p 2 ) ± z α / 2 π 1 ( 1 − π 1 ) n 1 + π 2 ( 1 − π 2 ) n 2 (p_1-p_2)\pm z_{\alpha/2}\sqrt{\frac{\pi_1(1-\pi_1)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2}} (p1−p2)±zα/2n1π1(1−π1)+n2π2(1−π2)
两个总体方差比的区间估计
F ( n 1 − 1 , n 2 − 1 ) F(n_1-1,n_2-1) F(n1−1,n2−1)

7.4 样本量的确定
估计总体均值时的样本量
令E代表所希望达到的标准误差, E = z α / 2 σ n E=z_{\alpha/2}\frac{\sigma}{\sqrt{n}} E=zα/2nσ
则样本量: n = ( z α / 2 ) 2 σ 2 E 2 n=\frac{(z_{\alpha/2})^2\sigma^2}{E^2} n=E2(zα/2)2σ2
估计总体比例时的样本量
E = z α / 2 π ( 1 − π ) n E=z_{\alpha/2}\frac{\pi(1-\pi)}{\sqrt{n}} E=zα/2nπ(1−π)
则样本量: n = ( z α / 2 ) 2 π ( 1 − π ) E 2 n=\frac{(z_{\alpha/2})^2\pi(1-\pi)}{E^2} n=E2(zα/2)2π(1−π)
8 假设检验
8.1 假设检验的基本问题
参数估计和假设检验都是利用样本对总体进行某种推断,推断的角度不同。
原假设(零假设) H 0 H_0 H0
备择假设 H 1 H_1 H1
原假设和备择假设互斥。假设检验是围绕着原假设是否成立而展开的。
两类错误:
一类错误:原假设 H 0 H_0 H0为真却被我们拒绝,犯这种错误的概率用 α \alpha α表示,也称 α \alpha α错误或弃真错误;
二类错误:原假设为伪我们却没有拒绝,犯这种错误的概率用 β \beta β表示,也称 β \beta β错误或取伪错误;
控制第一类错误的原因:原假设常常是明确的,备择假设是模糊的
进行假设检验利用的是小概率原理:值发生概率很小的随机事件在一次试验中是几乎不可能发生的。
如果原假设成立,那么在一次实验中z统计量落入两侧拒绝域的概率只有0.05,这个概率是很小的。这个情况出现则拒绝原假设,选择备择假设。
利用P值进行决策
意义:0.05是一个通用的风险概率,这是用域表示的弱点,但根据不同的样本结果进行决策,面临的风险事实上是有差别的,为了精确的反映决策的风险度,可以利用P值决策。
定义:P值就是当原假设为真时所得到的样本观察结果或者更极端结果出现的概率。P值越小,拒绝原假设的理由就更充分。
P值大小取决于三个因素:1.样本数据与原假设之间的差异;2.样本量;3.被假设参数的总体分布。
P值长处:反映了观察到的实际数据与原假设之间不一致的概率值。双侧检验中 P < α / 2 P<\alpha/2 P<α/2拒绝原假设。P值本身就代表了显著性水平。
单侧检验
左侧检验:关注容忍的下限, H 0 ≥ μ H_0\geq\mu H0≥μ
右侧检验:确定拒绝的上限临界点, H 0 ≤ μ H_0\leq\mu H0≤μ
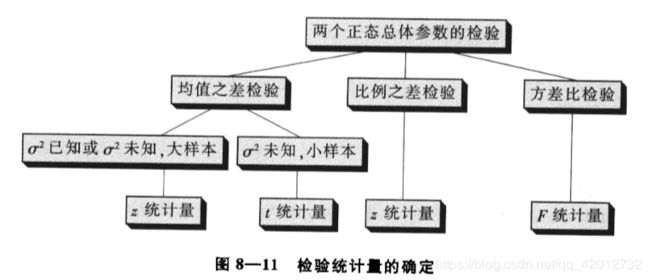
8.2 一个总体参数的检验
统计量:z统计量,t统计量, χ 2 \chi^2 χ2统计量
z统计量,t统计量常用于均值和比例的检验。
χ 2 \chi^2 χ2统计量用于方差的检验。
z = x ˉ − μ 0 σ / n z=\frac{\bar{x}-\mu_0}{\sigma/\sqrt{n}} z=σ/nxˉ−μ0
t = x ˉ − μ 0 s / n t=\frac{\bar{x}-\mu_0}{s/\sqrt{n}} t=s/nxˉ−μ0
显著性水平: α \alpha α当原假设正确是却被拒绝的概率或风险。
一个小样本, σ \sigma σ已知的单侧检验的例子:


总体方差检验
由于 s 2 = ∑ ( x i − x ˉ ) 2 n − 1 s^2=\frac{\sum(x_i-\bar{x})^2}{n-1} s2=n−1∑(xi−xˉ)2
∑ ( x i − x ˉ ) 2 = ( n − 1 ) s 2 \sum(x_i-\bar{x})^2=(n-1)s^2 ∑(xi−xˉ)2=(n−1)s2
∑ ( x i − x ˉ ) 2 σ 2 = ( n − 1 ) s 2 σ 2 \frac{\sum(x_i-\bar{x})^2}{\sigma^2}=\frac{(n-1)s^2}{\sigma^2} σ2∑(xi−xˉ)2=σ2(n−1)s2 服从 χ 2 \chi^2 χ2分布
则 χ 2 = ( n − 1 ) s 2 σ 2 \chi^2=\frac{(n-1)s^2}{\sigma^2} χ2=σ2(n−1)s2
总体方差检验的例子:

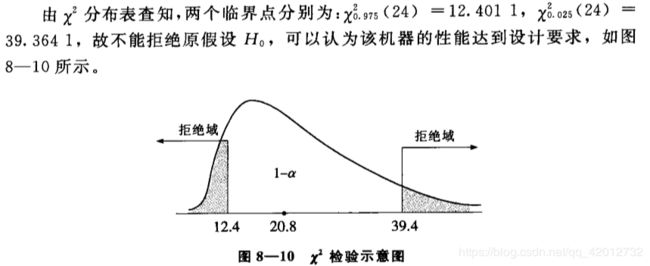
接受备择假设意味着原假设错误,没有拒绝原假设并不能表明备择假设一定是错误的。

