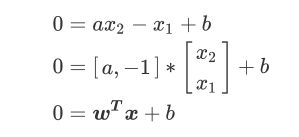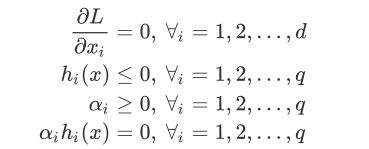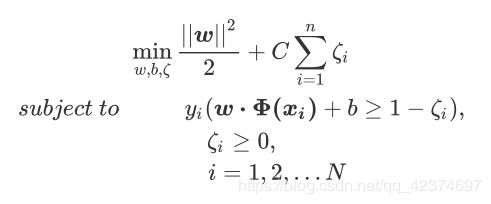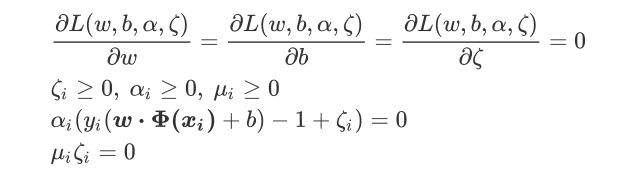sklearn_支持向量机SVM(1)
菜菜的scikit-learn课堂——sklearn中的支持向量机SVM(上)
文章目录
- 1 概述
- 1.1 支持向量机分类器是如何工作的
- 1.2 支持向量机原理的三层理解
- 1.3 sklearn中的支持向量机
- 2 sklearn.svm.SVC
- 2.1 线性SVM用于分类的原理
- 2.1.1 线性SVM的损失函数
- 2.1.2 函数间隔与几何间隔
- 2.1.3 线性SVM的拉格朗日对偶函数和决策函数
- 2.1.3.1 将损失函数从最初形态转换为拉格朗日乘数形态
- 2.1.3.2 将拉格朗日函数转换为拉格朗日对偶函数
- 2.1.3.3 求解拉格朗日对偶函数极其后续过程
- 2.1.4 线性SVM决策过程的可视化
- 2.2 非线性SVM与核函数
- 2.2.1 SVC在非线性数据上的推广
- 2.2.2 重要参数kernel
- 2.2.3 探索核函数在不同数据集上的表现
- 2.2.4 探索核函数的优势和缺陷
- 2.2.5 选取与核函数相关的参数:degree & gamma & coef0
- 2.3 硬间隔与软间隔:重要参数C
- 2.3.1 SVM在软间隔数据上的推广
- 2.3.2 重要参数C
1 概述
支持向量机(support vector machines),简称SVM(也称为支持向量网络),是机器学习中获得关注最多的算法没有之一。
SVM是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解,是一个强学习器。
传统的统计模式识别方法只有在样本趋向于无穷大时,其性能才有理论的保证。统计学习理论(STL)研究有限样本情况下的机器学习问题。
SVM的理论基础就是统计学习理论。
| 功能 | |
|---|---|
| 有监督学习 | 线性二分类与多分类(Linear Support Vector Classification) 非线性二分类与多分类(Support Vector Classification, SVC) 普通连续型变量的回归(Support Vector Regression) 概率型连续变量的回归(Bayesian SVM) |
| 无监督学习 | 支持向量聚类(Support Vector Clustering,SVC) 异常值检测(One-class SVM) |
| 半监督学习 | 转导支持向量机(Transductive Support Vector Machines,TSVM) |
从分类效力来讲,SVM在无论线性还是非线性分类中,都是明星般的存在:

1.1 支持向量机分类器是如何工作的
SVM从线性可分情况下的最优分类面发展而来。最优分类面就是要求分类线不但能将两类正确分开(训练错误率为0),且使分类间隔最大。
SVM考虑寻找一个满足分类要求的超平面,并且使训练集中的点距离分类面尽可能的远,也就是寻找一个分类面使它两侧的空白区域(margin)最大。
这两类样本中离分类面最近,且平行于最优分类面的超平面上的点,就叫做支持向量(下图中红色的点)。
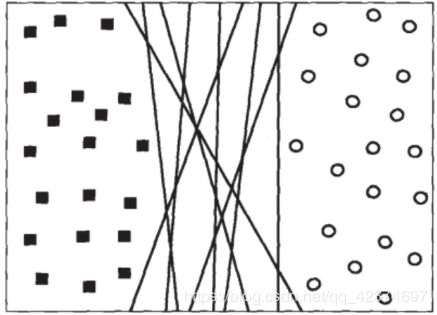
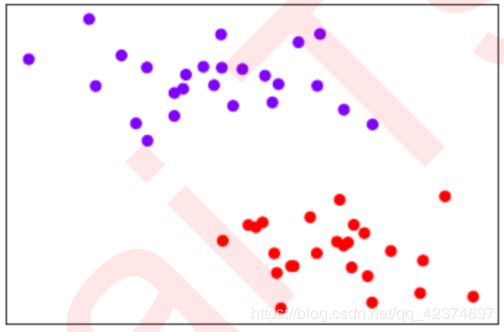
例如在一组两种标签的数据中,两种标签分别由圆和方块代表。
支持向量机的分类方法,就是在这组分布中找出一个超平面作为决策边界,使模型在数据上的分类误差尽量接近于小,尤其是在未知数据集上的分类误差(泛化误差)尽量小。
| 关键概念:超平面 |
|---|
| 在几何中,超平面是一个空间的子空间,它是维度比所在空间小一维的空间。 如果数据空间本身是三维的,则其超平面是二维平面,而如果数据空间本身是二维的,则其超平面是一维的直线。在二分类问题中,如果一个超平面能够将数据划分为两个集合,其中每个集合中包含单独的一个类别,我们就说这个超平面是数据的“决策边界”。 |
决策边界一侧的所有点在分类为属于一个类,而另一侧的所有点分类属于另一个类。
如果能够找出决策边界,分类问题就可以变成探讨每个样本对于决策边界而言的相对位置。比如上面的数据分布,我们很容易就可以在方块和圆的中间画出一条线,并让所有落在直线左边的样本被分类为方块,在直线右边的样本被分类为圆。
如果把数据当作训练集,只要直线的一边只有一种类型的数据,就没有分类错误,训练误差就会为0。
但是,对于一个数据集来说,让训练误差为0的决策边界可以有无数条。
但在此基础上,无法保证这条决策边界在未知数据集(测试集)上的表现也会优秀。
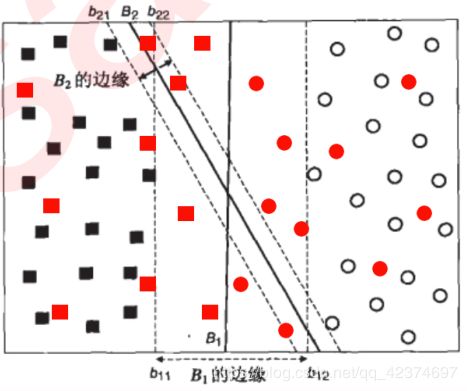
对于现有的数据集来说,有 B 1 B_1 B1 和 B 2 B_2 B2 两条可能的决策边界。
我们可以把决策边界 B 1 B_1 B1 向两边平移,直到碰到离这条决策边界最近的样本(最近的方块和圆圈后)停下,形成两个新的超平面,分别是 b 11 b_{11} b11 和 b 12 b_{12} b12 ,并且将原始的决策边界移动到 b 11 b_{11} b11 和 b 12 b_{12} b12 的中间,确保 B 1 B_1 B1 到 b 11 b_{11} b11 和 b 12 b_{12} b12 的距离相等。在 b 11 b_{11} b11 和 b 12 b_{12} b12 中间的距离,叫做 B 1 B_1 B1 这条决策边界的边际(margin),通常记作 d d d。为了简便,称 b 11 b_{11} b11 和 b 12 b_{12} b12 为“虚线超平面”。
对 B 2 B_2 B2 也执行同样的操作,然后来对比一下两个决策边界。
现在两条决策边界右边的数据都被判断为圆,左边的数据都被判断为方块,两条决策边界在现在的数据集上的训练误差都是0,没有一个样本被分错。
引入和原本的数据集相同分布的测试样本(红色所示),平面中的样本变多了,此时我们可以发现,对于 B 1 B_1 B1 而言,依然没有一个样本被分错,这条决策边界上的泛化误差也是0。但是对于 B 2 B_2 B2 而言,却有三个方块被误分类成圆,二有两个圆被误分类成了方块,这条决策边界上的泛化误差就远远大于 B 1 B_1 B1 了。
也就是说,拥有更大边际的决策边界在分类中的泛化误差更小,这一点可以由结构风险最小化定律来证明(SRM)。
如果边际很小,则任何轻微扰动都会对决策边界的分类产生很大的影响。边际很小的情况,是一种模型在训练集上表现很好,却在测试集上表现糟糕的情况,所以会“过拟合”。所以我们在找寻决策边界的时候,希望边际越大越好。
支持向量机,就是通过找出边际最大的决策边界,来对数据进行分类的分类器。也因此,支持向量分类器又叫做最大边际分类器。这个过程在二维平面中看起来十分简单,但将上述过程使用数学表达出来,就不是一件简单的事情了。
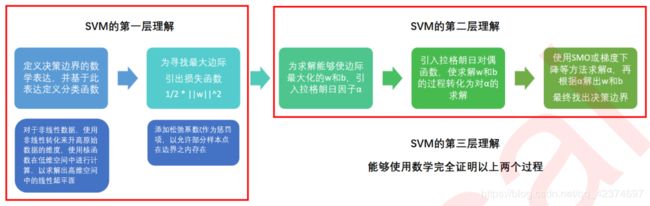
1.2 支持向量机原理的三层理解
目标是"找出边际最大的决策边界",听起来是一个十分熟悉的表达,这是一个最优化问题,而最优化问题往往和损失函数联系在一起。和逻辑回归中的过程一样,SVM也是通过最小化损失函数来求解一个用于后续模型使用的重要信息:决策边界。
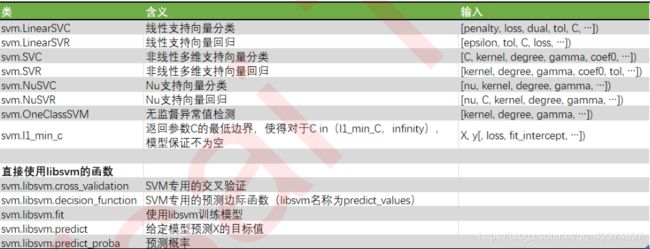
1.3 sklearn中的支持向量机
2 sklearn.svm.SVC
class sklearn.svm.SVC (
C=1.0,
kernel='rbf',
degree=3,
gamma='auto_deprecated',
coef0=0.0,
shrinking=True,
probability=False,
tol=0.001,
cache_size=200,
class_weight=None,
verbose=False,
max_iter=-1,
decision_function_shape=’ovr’,
random_state=None)
2.1 线性SVM用于分类的原理
2.1.1 线性SVM的损失函数
要理解SVM的损失函数,我们先来定义决策边界。
假设现在数据中总计有 N N N 个训练样本,每个训练样本 i i i 可以被表示为 ( x i , y i ) ( i = 1 , 2 , ⋯ , N ) (x_i,y_i)(i=1,2,\cdots ,N) (xi,yi)(i=1,2,⋯,N) ,其中 x i x_i xi 是 ( x 1 i , x 2 i , ⋯ , x n i ) T \left( x_{1i},x_{2i},\cdots ,x_{ni} \right) ^T (x1i,x2i,⋯,xni)T 这样的一个特征向量,每个样本总共含有 n n n 个特征。
二分类标签 y i y_i yi 的取值是{-1, 1}。
如果 n n n 等于2,则有 i = ( x 1 i , x 2 i , y i ) T i=\left( x_{1i},x_{2i},y_i \right) ^T i=(x1i,x2i,yi)T ,分别由我们的特征向量和标签组成。此时我们可以在二维平面上,以 x 2 x_2 x2 为横坐标, x 1 x_1 x1 为纵坐标, y y y 为颜色,来可视化所有的 N N N 个样本:
让所有紫色点的标签为1,红色点的标签为-1。我们要在这个数据集上寻找一个决策边界,在二维平面上,决策边界(超平面)就是一条直线。二维平面上的任意一条线可以被表示为:
x 1 = a x 2 + b x_1=ax_2+b x1=ax2+b
其中 [a, -1] 为参数向量 ω \omega ω , x \boldsymbol{x} x 为特征向量, b b b 为截距。
注意,这个表达式长得非常像我们线性回归的公式:
y ( x ) = θ T x + θ 0 y\left( x \right) =\boldsymbol{\theta }^{\boldsymbol{T}}\boldsymbol{x}+\theta _0 y(x)=θTx+θ0
线性回归中等号的一边是标签,回归过后会拟合出一个标签,而决策边界的表达式中却没有标签的存在,全部是由参数,特征和截距组成的一个式子,等号的一边是0。
在一组数据下,
给定固定的 ω \omega ω 和 b b b,这个式子就可以是一条固定直线,在 ω \omega ω 和 b b b 不确定的状况下,这个表达式就可以代表平面上的任意一条直线。
如果在 ω \omega ω 和 b b b 固定时,给定一个唯一的 x \boldsymbol{x} x 的取值,这个表达式就可以表示一个固定的点。
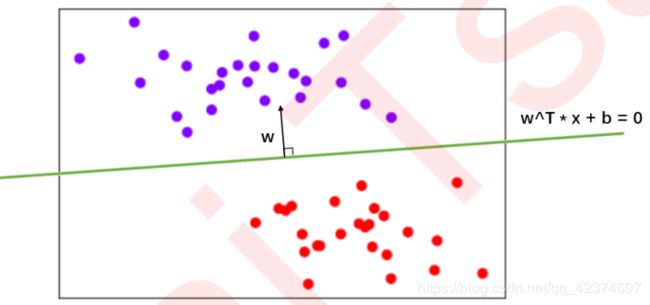
在SVM中使用这个表达式来表示决策边界。我们的目标是求解能够让边际最大化的决策边界,所以我们要求解参数向量 ω \omega ω 和截距 b b b 。
如果在决策边界上任意取两个点 x a \boldsymbol{x}_{\boldsymbol{a}} xa, x b \boldsymbol{x}_{\boldsymbol{b}} xb ,并带入决策边界的表达式,则有:
∣ ω T x a + b = 0 ω T x b + b = 0 \left| \begin{array}{l} \boldsymbol{\omega }^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{a}}+b=0\\ \\ \boldsymbol{\omega }^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{b}}+b=0\\ \end{array} \right. ∣∣∣∣∣∣ωTxa+b=0ωTxb+b=0
将两式相减,可以得到:
ω T ( x a − x b ) = 0 \boldsymbol{\omega }^{\boldsymbol{T}}\left( \boldsymbol{x}_{\boldsymbol{a}}-\boldsymbol{x}_b \right) =0 ωT(xa−xb)=0
一个列向量的转至乘以另一个列向量,可以获得两个向量的点积(dot product),表示为 < ω ⋅ ( x a − x b ) > \left< \omega \cdot \left( x_a-x_b \right) \right> ⟨ω⋅(xa−xb)⟩。
两个向量的点击为0表示两个向量的方向式互相垂直的。 x a \boldsymbol{x}_{\boldsymbol{a}} xa 与 x b \boldsymbol{x}_{\boldsymbol{b}} xb 是一条直线上的两个点,相减后的得到的向量方向是由 x b \boldsymbol{x}_{\boldsymbol{b}} xb 指向 x a \boldsymbol{x}_{\boldsymbol{a}} xa ,所以 x a − x b \boldsymbol{x}_{\boldsymbol{a}}-\boldsymbol{x}_{\boldsymbol{b}} xa−xb 的方向是平行于他们所在的直线——决策边界。而 ω \boldsymbol{\omega } ω 与 x a − x b \boldsymbol{x}_{\boldsymbol{a}}-\boldsymbol{x}_{\boldsymbol{b}} xa−xb 相互垂直,所以参数向量 ω \boldsymbol{\omega } ω 的方向必然是垂直于决策边界。
此时,我们有了我们的决策边界。任意一个紫色的点 x p \boldsymbol{x}_{\boldsymbol{p}} xp 就可以被表示为(不在直线上,所以不等于0):
ω ⋅ x p + b = p \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{p}}+b=p ω⋅xp+b=p
由于紫色的点所代表的标签y是1,所以规定,p>0。
同样的,对于任意一个红色的点 x r \boldsymbol{x}_{\boldsymbol{r}} xr 而言,我们可以将它表示为:
ω ⋅ x r + b = r \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{r}}+b=r ω⋅xr+b=r
由于红色点所表示的标签y是-1,所以规定,r<0。
由此,如果我们有新的测试数据 x t \boldsymbol{x}_{\boldsymbol{t}} xt ,则 x t \boldsymbol{x}_{\boldsymbol{t}} xt 的标签就可以根据以下式子来判定:
y = { − 1 , i f ω ⋅ x t + b > 0 1 , i f ω ⋅ x t + b < 0 y=\left\{ \begin{array}{l} -1\text{,}if\,\,\boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{t}}+b>0\\ \\ 1\text{,}if\,\,\boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{t}}+b<0\\ \end{array} \right. y=⎩⎨⎧−1,ifω⋅xt+b>01,ifω⋅xt+b<0
注意,在这里, p p p 和 r r r 的符号是我们人为规定的。
为了推导和计算的简便,规定
- 标签是{-1,1}
- 决策边界以上的点,标签都为正,并且通过调整 ω \boldsymbol{\omega } ω 和 b b b 的符号,让这个点在 ω ⋅ x + b \boldsymbol{\omega }\cdot \boldsymbol{x}+b ω⋅x+b上得出的结果为正。
- 决策边界以下的点,标签都为负,并且通过调整 ω \boldsymbol{\omega } ω 和 b b b 的符号,让这个点在 ω ⋅ x + b \boldsymbol{\omega }\cdot \boldsymbol{x}+b ω⋅x+b上得出的结果为负。
结论:决策边界以上的点都为正,以下的点都为负,是为了计算简便而人为规定的。这种规定,不会影响对参数向量 ω \boldsymbol{\omega } ω 和截距 b b b 的求解。
之前说过,决策边界的两边要有两个超平面,这两个超平面在二维空间中就是两条平行线(就是虚线超平面),而它们之间的距离就是边际 d d d 。而决策边界位于这两条线的中间,所以这两条平行线必然是对称的。
令这两条平行线被表示为:
ω ⋅ x + b = k , ω ⋅ x + b = − k \boldsymbol{\omega }\cdot \boldsymbol{x}+b=k\text{,}\boldsymbol{\omega }\cdot \boldsymbol{x}+b=-k ω⋅x+b=k,ω⋅x+b=−k
两个表达式同时除以 k,则可以得到:
ω ⋅ x + b = 1 , ω ⋅ x + b = − 1 \boldsymbol{\omega }\cdot \boldsymbol{x}+b=1\text{,}\boldsymbol{\omega }\cdot \boldsymbol{x}+b=-1 ω⋅x+b=1,ω⋅x+b=−1
这就是我们平行于决策边界的两条线的表达式,表达式两边的1和-1分别表示了两条平行于决策边界的虚线到决策边界的相对距离。
例如
这两类样本中离分类面最近,且平行于最优分类面的超平面上的点,就叫做支持向量(下图中红色的点)。

此时,可以让这两条线分别过两类数据中距离我们的决策边界最近的点,这些点就被称为“支持向量”,而决策边界永远在这两条线的中间,所以可以被调整。
我们令紫色类的点为 x p \boldsymbol{x}_{\boldsymbol{p}} xp ,红色类的点为 x r \boldsymbol{x}_{\boldsymbol{r}} xr ,则可以得到:
ω ⋅ x p + b = 1 , ω ⋅ x r + b = − 1 \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{p}}+b=1\text{,}\boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{r}}+b=-1 ω⋅xp+b=1,ω⋅xr+b=−1
两个式子相减,则有:
ω ⋅ ( x p − x r ) = 2 \boldsymbol{\omega }\cdot \left( \boldsymbol{x}_{\boldsymbol{p}}-\boldsymbol{x}_{\boldsymbol{r}} \right) =2 ω⋅(xp−xr)=2
如下图所示, x p − x r \boldsymbol{x}_{\boldsymbol{p}}-\boldsymbol{x}_{\boldsymbol{r}} xp−xr 可表示为两点之间的连线,而边际 d d d 是平行于 ω \boldsymbol{\omega } ω 的,所以相当于是得到了三角型中的斜边,并且知道一条直角边的方向。
所以,将上述式子两边同时除以 ∥ ω ∥ \lVert \omega \rVert ∥ω∥ ,则可以得到:
ω ⋅ ( x p − x r ) ∥ ω ∥ = 2 ∥ ω ∥ ⇒ d = 2 ∥ ω ∥ \frac{\boldsymbol{\omega }\cdot \left( \boldsymbol{x}_{\boldsymbol{p}}-\boldsymbol{x}_{\boldsymbol{r}} \right)}{\lVert \omega \rVert}=\frac{2}{\lVert \omega \rVert}\Rightarrow d=\frac{2}{\lVert \omega \rVert} ∥ω∥ω⋅(xp−xr)=∥ω∥2⇒d=∥ω∥2

要最大化 d d d ,就求解 ω \boldsymbol{\omega } ω 的最小值。
极值问题可以相互转化,可以把求解 ω \boldsymbol{\omega } ω 的最小值转化为,求解以下函数的最小值:
f ( ω ) = ∥ ω ∥ 2 2 f\left( \omega \right) =\frac{\lVert \omega \rVert ^2}{2} f(ω)=2∥ω∥2
在模长上加上平方是因为模长的本质是一个距离,所以它是一个带根号的存在,对它取平方是为了消除根号
我们的两条虚线表示的超平面,是数据边缘所在的点。所以对于任意样本 i i i,我们可以把决策函数写作:
{ ω ⋅ x i + b ≥ 1 , i f y i = 1 ω ⋅ x i + b ≤ − 1 , i f y i = − 1 \left\{ \begin{array}{l} \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b\ge 1\text{,}if\ y_i=1\\ \\ \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b\le -1\text{,}if\ y_i=-1\\ \end{array} \right. ⎩⎨⎧ω⋅xi+b≥1,if yi=1ω⋅xi+b≤−1,if yi=−1
整理一下,可以把两个式子整合成:
y i ( ω ⋅ x i + b ) ≥ 1 , i = 1 , 2 , ⋯ , N y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) \ge 1\text{,}i=1,2,\cdots ,N yi(ω⋅xi+b)≥1,i=1,2,⋯,N
这个式子被称为“函数间隔”。
将函数间隔作为条件附加到我们的 f ( ω ) f\left( \omega \right) f(ω) 上,我们就得到了SVM的损失函数最初形态:
min ω , b ∥ ω ∥ 2 2 \underset{\omega ,b}{\min}\frac{\lVert \omega \rVert ^2}{2} ω,bmin2∥ω∥2
s u b j e c t t o y i ( ω ⋅ x i + b ) ≥ 1 , i = 1 , 2 , ⋯ , N subject\ to\ y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) \ge 1\text{,}i=1,2,\cdots ,N subject to yi(ω⋅xi+b)≥1,i=1,2,⋯,N
2.1.2 函数间隔与几何间隔
| 重要定义:函数间隔与几何间隔 |
|---|
| 对于给定的数据集T和超平面 ( ω , b ) \left( \omega ,b \right) (ω,b) ,定义超平面 ( ω , b ) \left( \omega ,b \right) (ω,b) 关于样本点 ( x i , y i ) \left( x_i,y_i \right) (xi,yi) 的函数间隔为: γ i = y i ( ω ⋅ x i + b ) \gamma _i=y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) γi=yi(ω⋅xi+b) 函数间隔可以表示分类预测的正确性以及确信度。再在这个函数间隔的基础上除以 ω \boldsymbol{\omega } ω 的模长 ∥ ω ∥ \lVert \omega \rVert ∥ω∥ 来得到几何间隔: γ i = y i ( ω ∥ ω ∥ ⋅ x i + b ∥ ω ∥ ) \gamma _i=y_i\left( \frac{\omega}{\lVert \omega \rVert}\cdot \boldsymbol{x}_{\boldsymbol{i}}+\frac{b}{\lVert \omega \rVert} \right) γi=yi(∥ω∥ω⋅xi+∥ω∥b) 几何间隔的本质其实是点 x i x_i xi 到超平面 ( ω , b ) \left( \omega ,b \right) (ω,b) ,即到我们的决策边界的带符号的距离(signed distance)。 |
几何间隔中, y i y_i yi 的取值是{-1, 1},所以并不影响整个表达式的大小,只影响方向。
而 ω x + b = 0 \omega x+b=0 ωx+b=0 是决策边界,所以直线带入 x i x_i xi 后再除以参数向量的模长,就可以得到点 x i x_i xi 到决策边界的距离。
2.1.3 线性SVM的拉格朗日对偶函数和决策函数
有了损失函数过后,就需要对损失函数进行求解。
之前得到了线性SVM损失函数的最初形态:
min ω , b ∥ ω ∥ 2 2 \underset{\omega ,b}{\min}\frac{\lVert \omega \rVert ^2}{2} ω,bmin2∥ω∥2
s u b j e c t t o y i ( ω ⋅ x i + b ) ≥ 1 , i = 1 , 2 , ⋯ , N subject\ to\ y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) \ge 1\text{,}i=1,2,\cdots ,N subject to yi(ω⋅xi+b)≥1,i=1,2,⋯,N
这个损失函数分为两部分:需要最小化的函数,以及参数求解后必须满足的约束条件。这是一个最优化问题。
2.1.3.1 将损失函数从最初形态转换为拉格朗日乘数形态
为什么要进行转换?
我们的目标是求解让损失函数最小化的 ω \boldsymbol{\omega } ω,但其实很容易看得出来,如果 ∥ ω ∥ \lVert \omega \rVert ∥ω∥ 为0, f ( ω ) f\left( \omega \right) f(ω) 必然最小了,但是,这是一个无效的值。
单纯让 f ( ω ) = ∥ ω ∥ 2 2 f\left( \omega \right) =\frac{\lVert \omega \rVert ^2}{2} f(ω)=2∥ω∥2 为0,是不能求解出合理的 ω \boldsymbol{\omega } ω 的,我们希望能够找出一种方式,能够让我们的条件 y i ( ω ⋅ x i + b ) ≥ 1 y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) \ge 1 yi(ω⋅xi+b)≥1 在计算中也被纳入考虑,一种业界认可的方法是使用拉格朗日乘数法(standard Lagrange multiplier method)。
我们的损失函数是二次的(quadratic),并且我们损失函数中的约束条件在参数 ω \omega ω 和 b b b 下是线性的,求解这样的损失函数被称为“凸优化问题”(convex optimization problem)。拉格朗日乘数法正好可以用来解决凸优化问题,这种方法也是业界常用的,用来解决带约束条件,尤其是带有不等式的约束条件的函数的数学方法。
首先第一步,需要使用拉格朗日乘数来将损失函数改写为考虑了约束条件的形式:
L ( ω , b , α ) = 1 2 ∥ ω ∥ 2 − ∑ i = 1 N α i ( y i ( ω ⋅ x i + b ) − 1 ) ( α i ≥ 0 ) L\left( \omega ,b,\alpha \right) =\frac{1}{2}\lVert \omega \rVert ^2-\sum_{i=1}^N{\alpha _i\left( y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) -1 \right)}\left( \alpha _i\ge 0 \right) L(ω,b,α)=21∥ω∥2−i=1∑Nαi(yi(ω⋅xi+b)−1)(αi≥0)
称为拉格朗日函数,其中 α i \alpha _i αi 就叫做拉格朗日乘数。
此时此刻,我们要求解的就不只有参数向量 ω \omega ω 和截距 b b b 了,我们也要求解拉格朗日乘数 α i \alpha _i αi ,而我们的 x i x_i xi 和 y i y_i yi 都是已知的特征矩阵和标签。
拉格朗日函数也分为两部分。
第一部分和我们原始的损失函数一样,第二部分呈现了带有不等式的约束条件。
我们希望, L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 不仅能够代表原有的损失函数 f ( ω ) f\left( \omega \right) f(ω) 和约束条件,还能够表示我们想要最小化损失函数来求解 ω \omega ω 和 b b b 的意图,所以我们要先以 α \alpha α 为参数,求解 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 的最大值,再以 ω \omega ω 和 b b b 为参数,求解 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 的最小值。
因此,我们的目标可以写作:
min ω , b max α i ≥ 0 L ( ω , b , α ) ( α i ≥ 0 ) \underset{\omega ,b}{\min}\underset{\alpha _i\ge 0}{\ \max}\ L\left( \omega ,b,\alpha \right) \ \left( \alpha _i\ge 0 \right) ω,bminαi≥0 max L(ω,b,α) (αi≥0)
首先,我们第一步先执行max,即最大化 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) ,那就有两种情况:
- 当 y i ( ω ⋅ x i + b ) > 1 y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) >1 yi(ω⋅xi+b)>1,函数的第二部分 ∑ i = 1 N α i ( y i ( ω ⋅ x i + b ) − 1 ) \sum_{i=1}^N{\alpha _i\left( y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) -1 \right)} ∑i=1Nαi(yi(ω⋅xi+b)−1) 就一定为正,式子 1 2 ∥ ω ∥ 2 \frac{1}{2}\lVert \omega \rVert ^2 21∥ω∥2 就要减去一个正数,此时若要最大化 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) ,则 α \alpha α 必须取到0。
- 当 y i ( ω ⋅ x i + b ) < 1 y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) <1 yi(ω⋅xi+b)<1 ,函数的第二部分 ∑ i = 1 N α i ( y i ( ω ⋅ x i + b ) − 1 ) \sum_{i=1}^N{\alpha _i\left( y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) -1 \right)} ∑i=1Nαi(yi(ω⋅xi+b)−1) 就一定为负,式子 1 2 ∥ ω ∥ 2 \frac{1}{2}\lVert \omega \rVert ^2 21∥ω∥2 就要减去一个负数,相当于加上一个正数,此时若要最大化 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) ,则 α \alpha α 必须取到正无穷。
若把函数第二部分当作一个惩罚项来看待,则
y i ( ω ⋅ x i + b ) > 1 y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) >1 yi(ω⋅xi+b)>1 时函数没有受到惩罚,
y i ( ω ⋅ x i + b ) < 1 y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) <1 yi(ω⋅xi+b)<1 时函数受到了极致的惩罚,即加上了一个正无穷项,函数整体永远不可能取到最小值。
所以第二步,我们执行min的命令,求解函数整体的最小值,我们就永远不能让 α \alpha α 必须取到正无穷的状况出现,即是说永远不让 y i ( ω ⋅ x i + b ) < 1 y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) <1 yi(ω⋅xi+b)<1 的状况出现,从而实现了求解最小值的同时让约束条件被满足。
现在, L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 就是新的损失函数,我们的目标是要通过先最大化,再最小化它来求解参数向量 ω \omega ω 和截距 b b b 的值。
2.1.3.2 将拉格朗日函数转换为拉格朗日对偶函数
- 为什么要进行转换?
要求极值,最简单的方法还是对参数求导后让一阶导数等于0。
先来试试看对拉格朗日函数求极值,在这里对参数向量 ω \omega ω 和截距 b b b 分别求偏导并且让其等于0。这个求导过程比较简单:
由于两个求偏导结果中都带有未知的拉格朗日乘数 ,因此我们还是无法求解出参数向量 ω \omega ω 和截距 b b b ,必须想出一种方法来求解拉格朗日乘数 。
幸运地是,拉格朗日函数可以被转换成一种只带有 α \alpha α ,而不带有参数向量 ω \omega ω 和截距 b b b 的形式,这种形式被称为拉格朗日对偶函数。
在对偶函数下,就可以求解出拉格朗日乘数 α \alpha α,然后带入到上面推导出的(1)和(2)式中来求解参数向量 ω \omega ω 和截距 b b b 。
- 为什么能够进行转换?
对于任何一个拉格朗日函数 L ( x , α ) = f ( x ) + ∑ i = 1 q α i h i ( x ) L\left( x,\alpha \right) =f\left( x \right) +\sum_{i=1}^q{\alpha _ih_i\left( x \right)} L(x,α)=f(x)+i=1∑qαihi(x) 都存在一个与它对应的对偶函数 g ( α ) g\left( \alpha \right) g(α) ,只带有拉格朗日乘数 α \alpha α 作为唯一的参数。
如果 L ( x , α ) L\left( x,\alpha \right) L(x,α) 的最优解存在并可以表示为 min x L ( x , α ) \underset{x}{\min}L\left( x,\alpha \right) xminL(x,α) ,并且对偶函数的最优解也存在并可以表示为 max α g ( α ) \underset{\alpha}{\max}g\left( \alpha \right) αmaxg(α) ,
则可以定义对偶差异(dual gap),即拉格朗日函数的最优解与其对偶函数的最优解之间的差值:
Δ = min x L ( x , α ) − max α g ( α ) \varDelta =\underset{x}{\min}L\left( x,\alpha \right) -\underset{\alpha}{\max}g\left( \alpha \right) Δ=xminL(x,α)−αmaxg(α)
如果 Δ = 0 \varDelta =0 Δ=0,则称 L ( x , α ) L\left( x,\alpha \right) L(x,α) 与其对偶函数之间存在强对偶关系(strong duality property),此时我们就可以通过求解其对偶函数的最优解来替代求解原始函数的最优解。
那强对偶关系什么时候存在呢?
拉格朗日函数必须满足KKT(Karush-Kuhn-Tucker)条件:
这里的条件其实都比较好理解。首先是所有参数的一阶导数必须为0,然后约束条件中的函数本身需要小于等于0,拉格朗日乘数需要大于等于0,以及约束条件乘以拉格朗日乘数必须等于0,即不同 i i i 的取值下,两者之中至少有一个为0。
当所有限制都被满足,则拉格朗日函数 L ( x , α ) L\left( x,\alpha \right) L(x,α) 的最优解与其对偶函数的最优解相等,我们就可以将原始的最优化问题转换成为对偶函数的最优化问题。
而不难注意到,对于损失函数 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 而言,KKT条件都是可以操作的。如果我们能够人为让KKT条件全部成立,就可以求解出 的对偶函数来解出 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α)。
之前我们已经让拉格朗日函数上对参数w和b的求导为0,得到了式子:
∑ i = 1 N α i y i x i = ω ( 1 ) \sum_{i=1}^N{\alpha _iy_i\boldsymbol{x}_{\boldsymbol{i}}=\boldsymbol{\omega \ \ }\left( 1 \right)} i=1∑Nαiyixi=ω (1)
∑ i = 1 N α i y i = 0 ( 2 ) \sum_{i=1}^N{\alpha _iy_i=0\ \ \left( 2 \right)} i=1∑Nαiyi=0 (2)
并且在函数中,通过先求解最大值再求解最小值的方法使得函数天然满足:
− ( y i ( ω ⋅ x i + b ) − 1 ) ≤ 0 ( 3 ) α i ≥ 0 ( 4 ) -\left( y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) -1 \right) \le 0\ \ \left( 3 \right) \ \ \boldsymbol{\alpha }_{\boldsymbol{i}}\ge 0\ \ \left( 4 \right) −(yi(ω⋅xi+b)−1)≤0 (3) αi≥0 (4)
所以接下来,只需要再满足一个条件:
α i ( y i ( ω ⋅ x i + b ) − 1 ) = 0 \alpha _i\left( y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) -1 \right) =0 αi(yi(ω⋅xi+b)−1)=0
这个条件其实很容易满足,能够让 y i ( ω ⋅ x i + b ) − 1 = 0 y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b \right) -1=0 yi(ω⋅xi+b)−1=0 的就是落在虚线的超平面上的样本点,即支持向量。
所有不是支持向量的样本点则必须满足 α i = 0 \alpha _i=0 αi=0 。满足这个式子说明求解的参数参数向量 ω \omega ω 和截距 b b b以及求解的超平面的存在,只与支持向量相关,与其他样本点都无关。
现在KKT的五个条件都得到了满足,可以使用 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 的对偶函数来求解 α \alpha α。
…
- 怎样进行转换?
首先让拉格朗日函数对参数 ω \omega ω 和截距 b b b 求导后的结果为0,本质是在探索拉格朗日函数的最小值。然后:
整理

∑ i = 1 N α i y i x i = ω ( 1 ) \sum_{i=1}^N{\alpha _iy_i\boldsymbol{x}_{\boldsymbol{i}}=\boldsymbol{\omega \ \ }\left( 1 \right)} i=1∑Nαiyixi=ω (1)
∑ i = 1 N α i y i = 0 ( 2 ) \sum_{i=1}^N{\alpha _iy_i=0\ \ \left( 2 \right)} i=1∑Nαiyi=0 (2)


函数 L d L_d Ld 就是我们的对偶函数。对所有存在对偶函数的拉格朗日函数我们有对偶差异如下表示:
Δ = min x L ( x , α ) − max α g ( α ) \varDelta =\underset{x}{\min}L\left( x,\alpha \right) -\underset{\alpha}{\max}g\left( \alpha \right) Δ=xminL(x,α)−αmaxg(α)
对于 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 和 L d L_d Ld ,则有:
Δ = min ω , b max α i ≥ 0 L ( ω , b , α ) − max α i ≥ 0 L d \varDelta =\underset{\omega ,b}{\min}\underset{\alpha _i\ge 0}{\max}L\left( \omega ,b,\alpha \right) -\underset{\alpha _i\ge 0}{\max}L_d Δ=ω,bminαi≥0maxL(ω,b,α)−αi≥0maxLd
求解对偶函数的过程其实是在求解 L ( ω , b , α ) L\left( \omega ,b,\alpha \right) L(ω,b,α) 的最小值,所以又可以把公式写成:
max α i ≥ 0 ( ∑ i = 1 N α i − 1 2 ∑ i , j = 1 N α i α j y i y j x i ⋅ x j ) \underset{\alpha _i\ge 0}{\max}\left( \sum_{i=1}^N{\alpha _i}-\frac{1}{2}\sum_{i,j=1}^N{\alpha _i\alpha _jy_iy_j\boldsymbol{x}_{\boldsymbol{i}}\cdot \boldsymbol{x}_{\boldsymbol{j}}} \right) αi≥0max(i=1∑Nαi−21i,j=1∑Nαiαjyiyjxi⋅xj)
2.1.3.3 求解拉格朗日对偶函数极其后续过程
到了这一步,我们就需要使用梯度下降,SMO或者二次规划来求解 α \alpha α
一旦求得了 α \alpha α 值,就可以使用求导后得到的(1)式求解 ω \omega ω,并可以使用(1)式和决策边界的表达式结合,得到下面的式子来求解 b b b :
∑ i = 1 N α i y i x i ∗ x + b = 0 \sum_{i=1}^N{\alpha _iy_i\boldsymbol{x}_{\boldsymbol{i}}*x}+b=0 i=1∑Nαiyixi∗x+b=0
当求得特征向量 ω \omega ω 和 b b b,我们就得到了决策边界的表达式,也就可以利用决策边界和其有关的超平面来进行分类了,决策函数就可以被写作:
f ( x t e s t ) = s i g n ( ω ⋅ x t e s t + b ) = s i g n ( ∑ i = 1 N α i y i x i ⋅ x t e s t + b ) f\left( x_{test} \right) =sign\left( \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{test}}+b \right) =sign\left( \sum_{i=1}^N{\alpha _iy_i\boldsymbol{x}_{\boldsymbol{i}}\cdot \boldsymbol{x}_{\boldsymbol{test}}+b} \right) f(xtest)=sign(ω⋅xtest+b)=sign(i=1∑Nαiyixi⋅xtest+b)
其中 x t e s t x_{test} xtest 是任意测试样本, s i g n sign sign 是 h > 0 h>0 h>0 时返回1, h < 0 h<0 h<0 时返回-1的符号函数。
2.1.4 线性SVM决策过程的可视化
可以使用sklearn中的式子来为可视化决策边界,支持向量,以及决策边界平行的两个超平面。
1. 导入需要的模块
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
2. 实例化数据集,可视化数据集
X,y = make_blobs(n_samples=50, centers=2, random_state=0,cluster_std=0.6)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.xticks([])
plt.yticks([])
plt.show()
matplotlib.axes.Axes.contour([X, Y,] Z, [levels], **kwargs)
Contour是专门用来绘制等高线的函数。
等高线,本质上是在二维图像上表现三维图像的一种形式,其中两维 X 和 Y 是两条坐标轴上的取值,而 Z 表示高度。
Contour就是将由 X 和 Y 构成平面上的所有点中,高度一致的点连接成线段的函数,在同一条等高线上的点一定具有相同的 Z 值。可以利用这个性质来绘制我们的决策边界。

我们的决策边界是 ω ⋅ x + b = 0 \boldsymbol{\omega }\cdot \boldsymbol{x}+b=0 ω⋅x+b=0 ,并在决策边界的两边找出两个超平面,使得超平面到决策边界的相对距离为1。
那其实,只需要在样本构成的平面上,把所有到决策边界的距离为0的点相连,就是我们的决策边界,而把所有到决策边界的相对距离为1的点相连,就是两个平行于决策边界的超平面了。此时,Z就是平面上的任意点到达超平面的距离。
那首先,我们需要获取样本构成的平面,作为一个对象。
#首先要有散点图
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
有了这个平面,我们需要在平面上制作一个足够细的网格,来代表我们“平面上的所有点”。
计算每一个网格数据点到决策边界的距离,这样就不用在两处样本点中去找满足条件的两个点来构成这个直线,解决没有两个点到这个直线的距离一致的话,就画不出这条等高线的问题
- 画决策边界:制作网格,理解函数meshgrid
两两组合
理解函数meshgrid和vstack的作用
a = np.array([1,2,3])
b = np.array([7,8])
#两两组合,会得到多少个坐标?
#答案是6个,分别是 (1,7),(2,7),(3,7),(1,8),(2,8),(3,8)
v1,v2 = np.meshgrid(a,b)
v1
'''
array([[1, 2, 3],
[1, 2, 3]])
'''
v2
'''
array([[7, 7, 7],
[8, 8, 8]])
'''
v = np.vstack([v1.ravel(), v2.ravel()]).T
v
'''
array([[1, 7],
[2, 7],
[3, 7],
[1, 8],
[2, 8],
[3, 8]])
'''
#获取平面上两条坐标轴的最大值和最小值
xlim = ax.get_xlim() # (-0.7425578984849813, 3.3721920271976598)
ylim = ax.get_ylim() # (-0.41872382476349596, 5.754870487889891)
#在最大值和最小值之间形成30个规律的数据
axisx = np.linspace(xlim[0],xlim[1],30)
'''
array([-0.7425579 , -0.60066997, -0.45878204, -0.31689411, -0.17500618,
-0.03311826, 0.10876967, 0.2506576 , 0.39254553, 0.53443346,
0.67632139, 0.81820931, 0.96009724, 1.10198517, 1.2438731 ,
1.38576103, 1.52764896, 1.66953689, 1.81142481, 1.95331274,
2.09520067, 2.2370886 , 2.37897653, 2.52086446, 2.66275238,
2.80464031, 2.94652824, 3.08841617, 3.2303041 , 3.37219203])
'''
axisy = np.linspace(ylim[0],ylim[1],30)
'''
array([-0.41872382, -0.20584126, 0.0070413 , 0.21992386, 0.43280643,
0.64568899, 0.85857155, 1.07145411, 1.28433668, 1.49721924,
1.7101018 , 1.92298436, 2.13586693, 2.34874949, 2.56163205,
2.77451461, 2.98739718, 3.20027974, 3.4131623 , 3.62604486,
3.83892743, 4.05180999, 4.26469255, 4.47757511, 4.69045768,
4.90334024, 5.1162228 , 5.32910536, 5.54198793, 5.75487049])
'''
axisy,axisx = np.meshgrid(axisy,axisx)
#我们将使用这里形成的二维数组作为我们contour函数中的X和Y
#使用meshgrid函数将两个一维向量转换为特征矩阵
#核心是将两个特征向量广播,以便获取y.shape * x.shape这么多个坐标点的横坐标和纵坐标
axisx
'''
array([[-0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 ,
-0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 ,
-0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 ,
-0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 ,
-0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 ,
-0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 , -0.7425579 ],
[-0.60066997, -0.60066997, -0.60066997, -0.60066997, -0.60066997,
-0.60066997, -0.60066997, -0.60066997, -0.60066997, -0.60066997,
-0.60066997, -0.60066997, -0.60066997, -0.60066997, -0.60066997,
-0.60066997, -0.60066997, -0.60066997, -0.60066997, -0.60066997,
-0.60066997, -0.60066997, -0.60066997, -0.60066997, -0.60066997,
-0.60066997, -0.60066997, -0.60066997, -0.60066997, -0.60066997],
[-0.45878204, -0.45878204, -0.45878204, -0.45878204, -0.45878204,
-0.45878204, -0.45878204, -0.45878204, -0.45878204, -0.45878204,
....
'''
# 也就是
'''
-0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558 -0.742558
-0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067 -0.60067
-0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782 -0.458782
....
'''
axisx.shape # (30, 30)
xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
#其中ravel()是降维函数,vstack能够将多个结构一致的一维数组按行堆叠起来
#xy就是已经形成的网格,它是遍布在整个画布上的密集的点
xy.shape # (900, 2) 30*30=900 两两组合

有了网格后,我们需要计算网格所代表的“平面上所有的点”到我们的决策边界的距离。
所以需要模型和决策边界。
5. 建模,计算决策边界并找出网格上每个点到决策边界的距离
#建模,通过fit计算出对应的决策边界
clf = SVC(kernel = "linear").fit(X,y)
Z = clf.decision_function(xy).reshape(axisx.shape) # # 900个点计算出的到决策边界的所有距离
#重要接口decision_function,返回每个输入的样本所对应的到决策边界的距离
#然后再将这个距离转换为axisx的结构,这是由于画图的函数contour要求Z的结构必须与X和Y保持一致
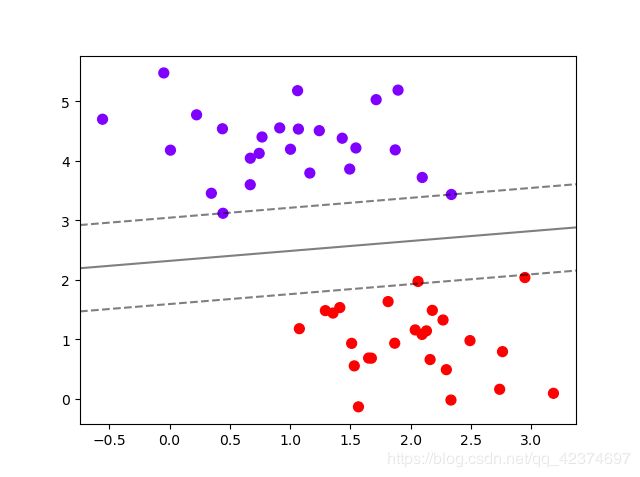
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
#画决策边界和平行于决策边界的超平面
ax.contour(
axisx,
axisy,
Z,
colors="k",
levels=[-1,0,1] #画三条等高线,分别是Z为-1,Z为0和Z为1的三条线
,alpha=0.5, # 透明度
linestyles=["--","-","--"])
ax.set_xlim(xlim) # (-0.7425578984849813, 3.3721920271976598)
ax.set_ylim(ylim) # (-0.41872382476349596, 5.754870487889891)
记得Z的本质么?是输入的样本到决策边界的距离,而contour函数中的level其实是输入了这个距离
随便用一个点来试试看
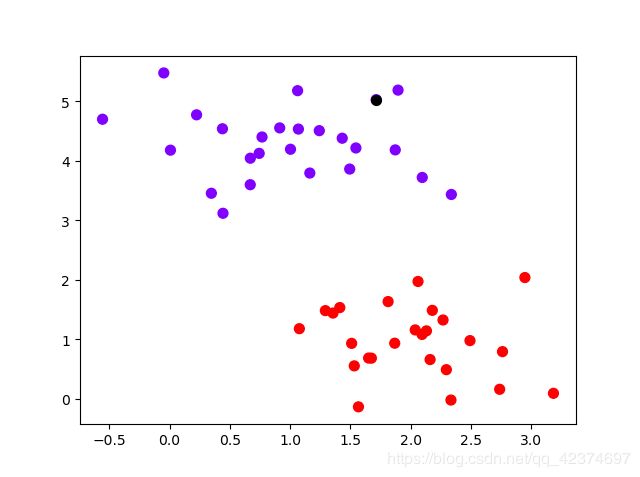
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
# 取第10的个点,让其为黑色
plt.scatter(X[10,0],X[10,1],c="black",s=50,cmap="rainbow")
# 计算这个点到决策边界的距离
clf.decision_function(X[10].reshape(1,2)) # array([-3.33917354])
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca()
ax.contour(
axisx,
axisy,
Z,
colors="k",
levels=[-3.33917354],
alpha=0.5,
linestyles=["--"])
- 将绘图过程包装成函数
#将上述过程包装成函数:
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
#则整个绘图过程可以写作:
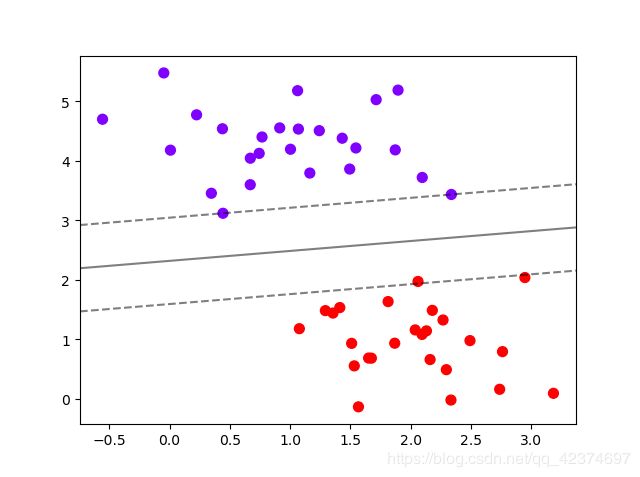
clf = SVC(kernel = "linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
clf.predict(X)
#根据决策边界,对X中的样本进行分类,返回的结构为n_samples
'''
array([1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1,
1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1,
0, 1, 1, 0, 1, 0])
'''
clf.score(Xtest,ytest)
# 返回给定测试数据和标签的平均准确度
clf.support_vectors_
#返回支持向量
# 这里是三个点
'''
array([[0.44359863, 3.11530945],
[2.33812285, 3.43116792],
[2.06156753, 1.96918596]])
'''
clf.n_support_
#返回每个类中支持向量的个数
# array([2, 1]) 第一个类中有两个支持向量,第二个中有两个支持向量
8. 推广到非线性情况
from sklearn.datasets import make_circles
X,y = make_circles(100, factor=0.1, noise=.1)
X.shape # (100, 2)
y.shape # (100,)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.show()
clf = SVC(kernel = "linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
clf.score(X,y)
# 0.7
明显,现在线性SVM已经不适合于我们的状况了,无法找出一条直线来划分我们的数据集,让直线的两边分别是两种类别。
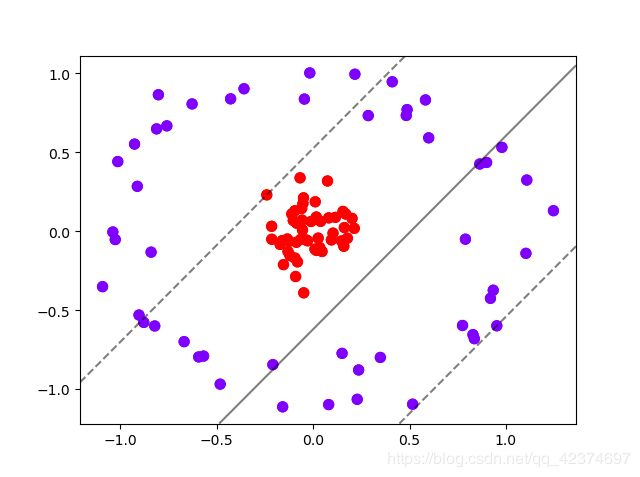
这个时候,如果我们能够在原本的X和y的基础上,添加一个维度r,变成三维,我们可视化这个数据,来看看添加维度让我们的数据如何变化。
9. 为非线性数据增加维度并绘制3D图像
#定义一个由x计算出来的新维度r
r = np.exp(-(X**2).sum(1))
rlim = np.linspace(min(r),max(r),100)
from mpl_toolkits import mplot3d
#定义一个绘制三维图像的函数
#elev表示上下旋转的角度
#azim表示平行旋转的角度
def plot_3D(elev=30,azim=30,X=X,y=y):
ax = plt.subplot(projection="3d")
ax.scatter3D(X[:,0],X[:,1],r,c=y,s=50,cmap='rainbow')
ax.view_init(elev=elev,azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("r")
plt.show()
plot_3D()

可以看见,此时此刻我们的数据明显是线性可分的了:我们可以使用一个平面来将数据完全分开,并使平面的上方的所有数据点为一类,平面下方的所有数据点为另一类。
将上述过程放到Jupyter Notebook中运行
from ipywidgets import interact,fixed
interact(plot_3D,elev=[0,30],azip=(-180,180),X=fixed(X),y=fixed(y))
plt.show()
此时数据在三维空间中,超平面就是一个二维平面。
明显我们可以用一个平面将两类数据隔开,这个平面就是我们的决策边界了。我们刚才做的,计算r,并将r作为数据的第三维度来将数据升维的过程,被称为“核变换”,即是将数据投影到高维空间中,以寻找能够将数据完美分割的超平面,即是说寻找能够让数据线性可分的高维空间。
引入SVM中的核心概念:核函数
2.2 非线性SVM与核函数
2.2.1 SVC在非线性数据上的推广
为了能够找出非线性数据的线性决策边界,需要将数据从原始的空间 x x x 投射到新空间 中 Φ ( x ) \varPhi \left( x \right) Φ(x)。
Φ \varPhi Φ 是一个映射函数,它代表了某种非线性的变换,如同我们之前所做过的使用 r r r 来升维一样,这种非线性变换看起来是一种非常有效的方式。使用这种变换,线性SVM的原理可以被很容易推广到非线性情况下,其推导过程和逻辑都与线性SVM一模一样,只不过在定义决策边界之前,我们必须先对数据进行升维度,即将原始的 x x x 转换成 Φ ( x ) \varPhi \left( x \right) Φ(x) 。
如此,非线性SVM的损失函数的初始形态为:
min ω , b 1 2 ∥ ω ∥ 2 \underset{\omega ,b}{\min}\ \frac{1}{2}\lVert \omega \rVert ^2 ω,bmin 21∥ω∥2
s t . y i ( ω ⋅ Φ ( x i ) + b ≥ 1 ) , i = 1 , 2 , ⋯ , N st.\ y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{i}} \right) +b\ge 1 \right) \ ,\ i=1,2,\cdots ,N st. yi(ω⋅Φ(xi)+b≥1) , i=1,2,⋯,N
同理,非线性SVM的拉格朗日函数和拉格朗日对偶函数也可得:
L ( ω , b , α ) = 1 2 ∥ ω ∥ 2 − ∑ i = 1 N α i ( y i ( ω ⋅ Φ ( x i ) + b ) − 1 ) L\left( \omega ,b,\alpha \right) =\frac{1}{2}\lVert \omega \rVert ^2-\sum_{i=1}^N{\alpha _i}\left( y_i\left( \boldsymbol{\omega }\cdot \boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{i}} \right) +b \right) -1 \right) L(ω,b,α)=21∥ω∥2−i=1∑Nαi(yi(ω⋅Φ(xi)+b)−1)
L d = ∑ i = 1 N α i − 1 2 ∑ i , j α i α j y i y j Φ ( x i ) Φ ( x j ) L_d=\sum_{i=1}^N{\alpha _i}-\frac{1}{2}\sum_{i,j}{\alpha _i\alpha _jy_iy_j\boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{i}} \right) \boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{j}} \right)} Ld=i=1∑Nαi−21i,j∑αiαjyiyjΦ(xi)Φ(xj)
使用同样的推导方式,让拉格朗日函数满足KKT条件,并在拉格朗日函数上对每个参数求导,经过和线性SVM相同的变换后,就可以得到拉格朗日对偶函数。同样使用梯度下降或SMO等方式对 α \alpha α 进行求解,最后可以求得决策边界,并得到最终的决策函数:
2.2.2 重要参数kernel
这种变换非常巧妙,但也带有一些实现问题。
首先,我们可能不清楚应该什么样的数据应该使用什么类型的映射函数来确保可以在变换空间中找出线性决策边界。极端情况下,数据可能会被映射到无限维度的空间中,这种高维空间可能不是那么友好,维度越多,推导和计算的难度都会随之暴增。
其次,即使已知适当的映射函数,我们想要计算类似于 Φ ( x i ) ⋅ Φ ( x t e s t ) \boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{i}} \right) \cdot \boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{test}} \right) Φ(xi)⋅Φ(xtest) 这样的点积,计算量可能会无比巨大,要找出超平面所付出的代价是非常昂贵的。
关键概念:核函数
而解决这些问题的数学方式,叫做“核技巧”(Kernel Trick),是一种能够使用数据原始空间中的向量计算来表示升维后的空间中的点积结果的数学方式。具体表现为, K ( u , v ) = Φ ( u ) ⋅ Φ ( v ) K\left( \boldsymbol{u,v} \right) =\boldsymbol{\Phi }\left( \boldsymbol{u} \right) \cdot \boldsymbol{\Phi }\left( \boldsymbol{v} \right) K(u,v)=Φ(u)⋅Φ(v) 。而这个原始空间中的点积函数 ,就被叫做“核函数”(Kernel Function)。
核函数能够解决三个问题:
第一,有了核函数之后,无需去担心 Φ \varPhi Φ 究竟应该是什么样,因为非线性SVM中的核函数都是正定核函数,它们都满足美世定律(Mercer’s theorem),确保了高维空间中任意两个向量的点积一定可以被低维空间中的这两个向量的某种计算来表示(多数时候是点积的某种变换)。
第二,使用核函数计算低维度中的向量关系比计算原本的 Φ ( x i ) ⋅ Φ ( x t e s t ) \boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{i}} \right) \cdot \boldsymbol{\Phi }\left( \boldsymbol{x}_{\boldsymbol{test}} \right) Φ(xi)⋅Φ(xtest) 要简单太多了。
第三,因为计算是在原始空间中进行,所以避免了维度诅咒的问题。
选用不同的核函数,就可以解决不同数据分布下的寻找超平面问题。
在SVC中,这个功能由参数“kernel”和一系列与核函数相关的参数来进行控制。参数“kernel"在sklearn中可选以下几种选项:
可以看出,除了选项"linear"之外,其他核函数都可以处理非线性问题。多项式核函数有次数d,
- 当d为1的时候,它就是在处理线性问题;
- 当d为更高次项的时候,它就是在处理非线性问题。
我们来看看模型找出的决策边界时什么样:
# 1. 导入需要的模块
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
# 2. 实例化数据集,可视化数据集
X,y = make_blobs(n_samples=50, centers=2, random_state=0,cluster_std=0.6)
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
clf = SVC(kernel = "rbf").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
from sklearn.datasets import make_circles
X,y = make_circles(100, factor=0.1, noise=.1)
X.shape # (100, 2)
y.shape # (100,)
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
clf = SVC(kernel = "rbf").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
2.2.3 探索核函数在不同数据集上的表现
除了"linear"以外的核函数都能够处理非线性情况,那究竟什么时候选择哪一个核函数呢?
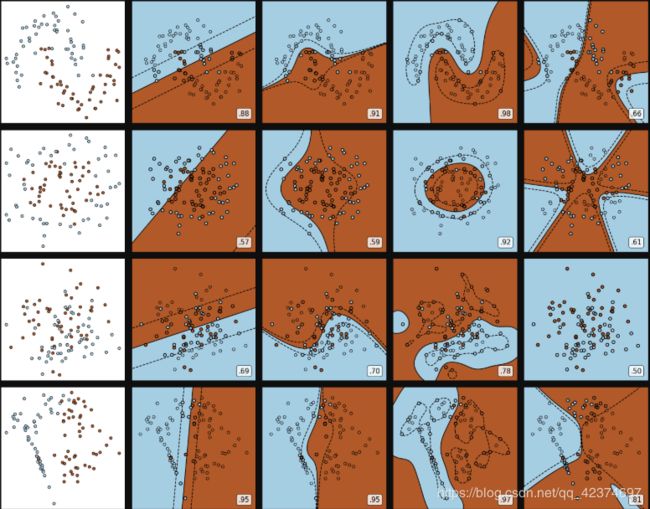
通过一个例子,来探索一下不同数据集上核函数的表现。我们现在有一系列线性或非线性可分的数据,我们希望通过绘制SVC在不同核函数下的决策边界并计算SVC在不同核函数下分类准确率来观察核函数的效用。
1. 导入所需要的库和模块
import numpy as np
import matplotlib.pyplot as plt
# 色彩块
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles, make_moons, make_blobs,make_classification
2. 创建数据集,定义核函数的选择
n_samples = 100
datasets = [
# 月亮
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
# 环
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
# 簇
make_blobs(n_samples=n_samples, centers=2, random_state=5),#分簇的数据集
# 分类
make_classification(n_samples=n_samples,n_features = 2,n_informative=2,n_redundant=0, random_state=5)
#n_features:特征数,n_informative:带信息的特征数,n_redundant:不带信息的特征数
]
Kernel = ["linear","poly","rbf","sigmoid"]
#四个数据集分别是什么样子呢?
for X,Y in datasets:
plt.figure(figsize=(5,4))
plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")
3. 构建子图
总共有四个数据集,四种核函数,我们希望观察每种数据集下每个核函数的表现。以核函数为列,以图像分布为行,我们总共需要16个子图来展示分类结果。而同时,我们还希望观察图像本身的状况,所以我们总共需要20个子图,其中第一列是原始图像分布,后面四列分别是这种分布下不同核函数的表现。
nrows=len(datasets)
ncols=len(Kernel) + 1
# 创建子图
fig, axes = plt.subplots(nrows, ncols,figsize=(20,16))
4. 开始进行子图循环
a = np.array([1,2,3])
b = np.array([7,8])
#两两组合,会得到多少个坐标?
#答案是6个,分别是 (1,7),(2,7),(3,7),(1,8),(2,8),(3,8)
v1,v2 = np.meshgrid(a,b)
v1
'''
array([[1, 2, 3],
[1, 2, 3]])
'''
v2
'''
array([[7, 7, 7],
[8, 8, 8]])
'''
v1.ravel() # array([1, 2, 3, 1, 2, 3])
v2.ravel() # array([7, 7, 7, 8, 8, 8])
v = np.vstack([v1.ravel(), v2.ravel()]).T
v
'''
array([[1, 7],
[2, 7],
[3, 7],
[1, 8],
[2, 8],
[3, 8]])
nrows=len(datasets)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(20,16))
#第一层循环:在不同的数据集中循环
# datasetsj结构
[*enumerate(datasets)] # enumerate、map、zip都可以使用 *+[] 展开
# index,(X,Y) = [(索引, array([特矩阵征X],[标签Y]))]
# 特矩阵征X (100.2)
# 标签Y (100,)
for ds_cnt, (X,Y) in enumerate(datasets):
#在图像中的第一列,放置原数据的分布
# ds_cnt 取0,1,2,3
ax = axes[ds_cnt, 0]
if ds_cnt == 0:
ax.set_title("Input data")
ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k')
ax.set_xticks(())
ax.set_yticks(())
#第二层循环:在不同的核函数中循环
#从图像的第二列开始,一个个填充分类结果
# enumerate(Kernel) 就是 索引+Kernel
for est_idx, kernel in enumerate(Kernel):
#定义子图位置
ax = axes[ds_cnt, est_idx + 1] # 行不动,列从第二列开始
#建模
clf = svm.SVC(kernel=kernel, gamma=2).fit(X, Y)
score = clf.score(X, Y)
#绘制图像本身分布的散点图
ax.scatter(X[:, 0], X[:, 1], c=Y
,zorder=10
,cmap=plt.cm.Paired,edgecolors='k')
#绘制支持向量
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=50,
facecolors='none', zorder=10, edgecolors='k')# facecolors='none':透明的
#绘制决策边界 ——网格 多一点点
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
#np.mgrid,合并了我们之前使用的np.linspace和np.meshgrid的用法
#一次性使用最大值和最小值来生成网格
#表示为[起始值:结束值:步长] j值把结束值包含在内
#如果步长是复数,则其整数部分就是起始值和结束值之间创建的点的数量,并且结束值被包含在内
# 网格
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
#np.c_,类似于np.vstack的功能 # ravel拉平 np.c_ 组合配对
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
#填充等高线不同区域的颜色
ax.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
#绘制等高线
ax.contour(XX,
YY,
Z,
colors=['k', 'k', 'k'],
linestyles=['--', '-', '--'],
levels=[-1, 0, 1])
#设定坐标轴为不显示
ax.set_xticks(())
ax.set_yticks(())
#将标题放在第一行的顶上
if ds_cnt == 0:
ax.set_title(kernel)
#为每张图添加分类的分数
ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0')
, size=15
, bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
#为分数添加一个白色的格子作为底色
, transform=ax.transAxes #确定文字所对应的坐标轴,就是ax子图的坐标轴本身
, horizontalalignment='right' #位于坐标轴的什么方向
)
plt.tight_layout() # 图像间隔紧缩
plt.show()
可以观察到,线性核函数和多项式核函数在非线性数据上表现会浮动,如果数据相对线性可分,则表现不错,如果是像环形数据那样彻底不可分的,则表现糟糕。
在线性数据集上,线性核函数和多项式核函数即便有扰动项也可以表现不错,可见多项式核函数是虽然也可以处理非线性情况,但更偏向于线性的功能。
Sigmoid核函数就比较尴尬了,它在非线性数据上强于两个线性核函数,但效果明显不如rbf,它在线性数据上完全比不上线性的核函数们,对扰动项的抵抗也比较弱,所以它功能比较弱小,很少被用到。
rbf,高斯径向基核函数基本在任何数据集上都表现不错,属于比较万能的核函数。
2.2.4 探索核函数的优势和缺陷
看起来,除了Sigmoid核函数,其他核函数效果都还不错。但其实rbf和poly都有自己的弊端,我们使用乳腺癌数据集作为例子来展示一下:
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from time import time
import datetime
data = load_breast_cancer()
X = data.data
y = data.target
X.shape # (569, 30)
np.unique(y) # array([0, 1])
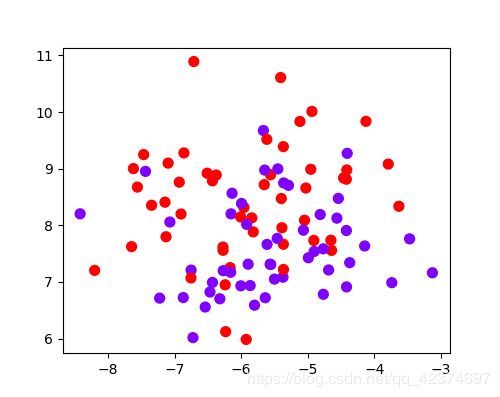
plt.scatter(X[:,0],X[:,1],c=y)
plt.show()
for kernel in Kernel:
time0 = time()
# 建模 实例化
clf= SVC(kernel = kernel
, gamma="auto"
# , degree = 1
, cache_size=10000#使用计算的内存,单位是MB,默认是200MB
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
多项式核函数此时此刻要消耗大量的时间,运算非常的缓慢。让我们在循环中去掉多项式核函数,再试试看能否跑出结果:
Kernel = ["linear","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
# , degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
The accuracy under kernel linear is 0.929825
0.8275289535522461
The accuracy under kernel rbf is 0.596491
0.07195615768432617
The accuracy under kernel sigmoid is 0.596491
0.007994651794433594
有两个发现。
首先,乳腺癌数据集是一个线性数据集,线性核函数跑出来的效果很好。rbf和sigmoid两个擅长非线性的数据从效果上来看完全不可用。
其次,线性核函数的运行速度远远不如非线性的两个核函数。如果数据是线性的,那如果我们把degree参数调整为1,多项式核函数应该也可以得到不错的结果:
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
, degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
The accuracy under kernel linear is 0.929825
0.7765562534332275
The accuracy under kernel poly is 0.923977
0.1239321231842041
The accuracy under kernel rbf is 0.596491
0.058963775634765625
The accuracy under kernel sigmoid is 0.596491
0.007994413375854492
多项式核函数的运行速度立刻加快了,并且精度也提升到了接近线性核函数的水平。
但是,之前的实验中,rbf 在线性数据上也可以表现得非常好,那在这里,为什么跑出来的结果如此糟糕呢?
其实,这里真正的问题是数据的量纲问题。
回忆一下如何求解决策边界,如何判断点是否在决策边界的一边?
是靠计算”距离“,虽然我们不能说SVM是完全的距离类模型,但是它严重受到数据量纲的影响。让我们来探索一下乳腺癌数据集的量纲:
import pandas as pd
data = pd.DataFrame(X)
data.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T#描述性统计
'''
count mean std ... 90% 99% max
0 569.0 14.127292 3.524049 ... 19.530000 24.371600 28.11000
1 569.0 19.289649 4.301036 ... 24.992000 30.652000 39.28000
2 569.0 91.969033 24.298981 ... 129.100000 165.724000 188.50000
3 569.0 654.889104 351.914129 ... 1177.400000 1786.600000 2501.00000
4 569.0 0.096360 0.014064 ... 0.114820 0.132888 0.16340
5 569.0 0.104341 0.052813 ... 0.175460 0.277192 0.34540
6 569.0 0.088799 0.079720 ... 0.203040 0.351688 0.42680
7 569.0 0.048919 0.038803 ... 0.100420 0.164208 0.20120
8 569.0 0.181162 0.027414 ... 0.214940 0.259564 0.30400
....
'''
#从mean列和std列可以看出严重的量纲不统一
#从1%的数据和最小值相对比,90%的数据和最大值相对比,查看是否是正态分布或偏态分布,如果差的太多就是偏态分布,谁大方向就偏向谁
#可以发现数据大的特征存在偏态问题
#这个时候就需要对数据进行标准化
数据存在严重的量纲不一的问题。使用数据预处理中的标准化的类,对数据进行标准化:
from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(X)#将数据转化为0,1正态分布
data = pd.DataFrame(X)
data.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T#均值很接近,方差为1了
'''
count mean std ... 90% 99% max
0 569.0 -3.162867e-15 1.00088 ... 1.534446 2.909529 3.971288
1 569.0 -6.530609e-15 1.00088 ... 1.326975 2.644095 4.651889
2 569.0 -7.078891e-16 1.00088 ... 1.529432 3.037982 3.976130
3 569.0 -8.799835e-16 1.00088 ... 1.486075 3.218702 5.250529
...
'''
标准化完毕后,再次让SVC在核函数中遍历,此时我们把degree的数值设定为1,观察各个核函数在去量纲后的数据上的表现:
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
, degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
The accuracy under kernel linear is 0.976608
0.01799154281616211
The accuracy under kernel poly is 0.964912
0.006995201110839844
The accuracy under kernel rbf is 0.970760
0.011993169784545898
The accuracy under kernel sigmoid is 0.953216
0.0059967041015625
量纲统一之后,可以观察到,所有核函数的运算时间都大大地减少了,尤其是对于线性核来说,而多项式核函数居然变成了计算最快的。其次,rbf表现出了非常优秀的结果。经过我们的探索,我们可以得到的结论是:
- 线性核,尤其是多项式核函数在高次项时计算非常缓慢
- r b f rbf rbf 和多项式核函数都不擅长处理量纲不统一的数据集
这两个缺点都可以由数据无量纲化来解决。因此,SVM执行之前,非常推荐先进行数据的无量纲化!到了这一步,我们是否已经完成建模了呢?虽然线性核函数的效果是最好的,但它是没有核函数相关参数可以调整的,rbf和多项式却还有着可以调整的相关参数,接下来我们就来看看这些参数。
2.2.5 选取与核函数相关的参数:degree & gamma & coef0
在知道如何选取核函数后,还要观察一下除了kernel之外的核函数相关的参数。
对于线性核函数,"kernel"是唯一能够影响它的参数,但是对于其他三种非线性核函数,还受到参数gamma,degree以及coef0的影响。
- 参数 gamma 就是表达式中的 γ \gamma γ
- 参数 degree 就是多项式核函数的次数 d d d
- 参数 coef0 就是常数项 r r r
其中,高斯径向基核函数受到 gamma 的影响,而多项式核函数受到全部三个参数的影响。
往往避免去真正探究这些参数如何影响了核函数,而直接使用学习曲线或者网格搜索来帮助我们查找最佳的参数组合。
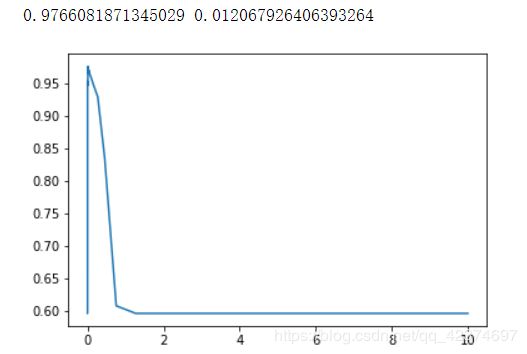
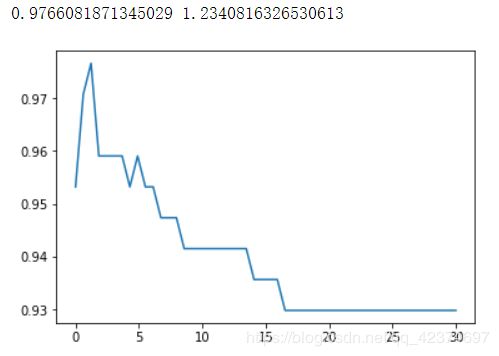
对于高斯径向基核函数,调整 gamma 的方式其实比较容易,那就是画学习曲线。我们来试试看高斯径向基核函数 rbf 的参数 gamma 在乳腺癌数据集上的表现:
score = []
gamma_range = np.logspace(-10, 1, 50) #返回在对数刻度上均匀间隔的数字
for i in gamma_range:
clf = SVC(kernel="rbf",gamma = i,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), gamma_range[score.index(max(score))])
plt.plot(gamma_range,score)
plt.show()
通过学习曲线,很容就找出了 rbf 的最佳 gamma 值。
但对于多项式核函数来说,一切就没有那么容易了,因为三个参数共同作用在一个数学公式上影响它的效果,因此,我们往往使用网格搜索来共同调整三个对多项式核函数有影响的参数。依然使用乳腺癌数据集。
from sklearn.model_selection import StratifiedShuffleSplit#用于支持带交叉验证的网格搜索
from sklearn.model_selection import GridSearchCV#带交叉验证的网格搜索
time0 = time()
gamma_range = np.logspace(-10,1,20)
coef0_range = np.linspace(0,5,10)
param_grid = dict(gamma = gamma_range
,coef0 = coef0_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.3, random_state=420)#将数据分为5份,5份数据中测试集占30%
grid = GridSearchCV(SVC(kernel = "poly",degree=1,cache_size=5000
,param_grid=param_grid
,cv=cv)
grid.fit(X, y)
print("The best parameters are %s with a score of %0.5f" % (grid.best_params_,
grid.best_score_))
print(time()-time0)
The best parameters are {'coef0': 0.0, 'gamma': 0.18329807108324375} with a score of 0.96959
13.360332727432251
可以发现,网格搜索返回了参数 coef0=0,gamma=0.18329807108324375,但整体的分数是0.96959,虽然比调参前略有提高,但依然没有超过线性核函数核rbf的结果。可见,如果最初选择核函数的时候,你就发现多项式的结果不如 rbf 和线性核函数,那就不要挣扎了,试试看调整 rbf 或者直接使用线性。
2.3 硬间隔与软间隔:重要参数C
2.3.1 SVM在软间隔数据上的推广
目前已经了解了线性SVC的基本原理,以及SVM如何被推广到非线性情况下,还了解了核函数的选择和应用。
但实际上,依然没有完全了解sklearn当中的SVM用于二分类的全貌。
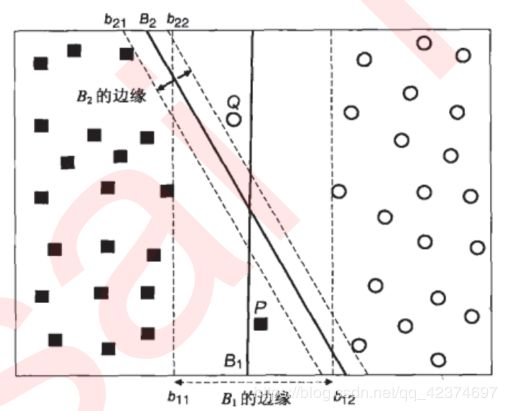
我们之前在理论推导中使用的数据都有一个特点,那就是它们或是完全线性可分,或者是非线性的数据。在对比核函数时,实际上用到了一种不同的数据,那就是不完全线性可分的数据集。比如说如下数据集:
这个数据集和最开始介绍SVM如何工作的时候的数据集一模一样,除了多了P和Q两个点。
注意到,虽然决策边界 B 1 B_1 B1 的间隔已经非常宽了,然而点 P 和 Q 依然被分错了类别,相反,边际比较小的 B 2 B_2 B2 却正确地分出了点 P 和 Q 的类别。
这里并不是说 B 2 B_2 B2 此时此刻就是一条更好的边界了,与之前的论述中一致,如果我们引入更多的训练数据,或引入测试数据, 更加宽敞的边界可以帮助它又更好的表现。但是,和之前不一样,现在即便是让边际最大的决策边界 B 1 B_1 B1 的训练误差也不可能为0了。此时,需要引入“软间隔”的概念:
关键概念:硬间隔与软间隔
-
当两组数据是完全线性可分,我们可以找出一个决策边界使得训练集上的分类误差为0,这两种数据就被称为是存在”硬间隔“的。
-
当两组数据几乎是完全线性可分的,但决策边界在训练集上存在较小的训练误差,这两种数据就被称为是存在”软间隔“。
可以通过调整对决策边界的定义,将硬间隔时得出的数学结论推广到软间隔的情况上,让决策边界能够忍受一小部分训练误差。这个时候决策边界就不是单纯地寻求最大边际了,因为对于软间隔地数据来说,边际越大被分错的样本也就会越多,因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。
在上图,原始的决策边界 ω ⋅ x + b = 0 \boldsymbol{\omega }\cdot \boldsymbol{x}+b=0 ω⋅x+b=0原本的平行于决策边界的两个虚线超平面 ω ⋅ x + b = 1 \boldsymbol{\omega }\cdot \boldsymbol{x}+b=1 ω⋅x+b=1 和 ω ⋅ x + b = − 1 \boldsymbol{\omega }\cdot \boldsymbol{x}+b=-1 ω⋅x+b=−1 都依然有效。
原始判别函数为:
{ ω ⋅ x i + b ≥ 1 , i f y i = 1 ω ⋅ x i + b ≤ − 1 , i f y i = − 1 \left\{ \begin{array}{l} \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b\ge 1\text{,}if\ \ y_i=1\\ \\ \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b\le -1\text{,}if\ \ y_i=-1\\ \end{array} \right. ⎩⎨⎧ω⋅xi+b≥1,if yi=1ω⋅xi+b≤−1,if yi=−1
不过,这些超平面现在无法让数据上的训练误差等于0了,因为此时存在了一个混杂在红色点中的紫色点 。
因此,需要放松原始判别函数中的不等条件,来让决策边界能够适用于异常点,于是引入松弛系数 ζ \zeta ζ 来帮助我们优化原始的判别函数:
{ ω ⋅ x i + b ≥ 1 − ζ i , i f y i = 1 ω ⋅ x i + b ≤ − 1 + ζ i , i f y i = − 1 \left\{ \begin{array}{l} \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b\ge 1-\zeta _i\text{,}if\,\,\,\,y_i=1\\ \\ \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b\le -1+\zeta _i\text{,}if\,\,\,\,y_i=-1\\ \end{array} \right. ⎩⎨⎧ω⋅xi+b≥1−ζi,ifyi=1ω⋅xi+b≤−1+ζi,ifyi=−1
其中 ζ i > 0 \zeta _i>0 ζi>0 。可以看得出,这其实是将原本的虚线超平面向图像的上方和下方平移,其符号的处理方式和原本的把符号放入 ω \boldsymbol{\omega } ω 是一模一样的方式。
ζ \boldsymbol{\zeta } ζ 可以作为点 x p x_p xp 在原始的决策边界上的分类错误的程度的表示,隔得越远,分得越错。但 ζ \boldsymbol{\zeta } ζ 并不是点到决策超平面的距离本身。
不难注意到,让 ω ⋅ x i + b ≥ 1 − ζ \boldsymbol{\omega }\cdot \boldsymbol{x}_{\boldsymbol{i}}+b\ge 1-\boldsymbol{\zeta } ω⋅xi+b≥1−ζ 作为新决策超平面,是由一定的问题的,虽然我们把异常的紫色点分类正确了,但同时也分错了一系列红色的点。
所以,必须在我们求解最大边际的损失函数中加上一个惩罚项,用来惩罚具有巨大松弛系数的决策超平面。拉格朗日函数,拉格朗日对偶函数,也因此都被松弛系数改变。现在,损失函数为:
拉格朗日函数为(其中 μ \mu μ 是第二个拉格朗日乘数):
以上所有的公式,是以线性硬间隔数据为基础,考虑了软间隔存在的情况和数据是非线性的状况而得来的。
而这些公式,就是sklearn类SVC背后使用的最终公式。公式中现在唯一的新变量,松弛系数的惩罚力度C,由参数C来进行控制。
2.3.2 重要参数C
参数C用于权衡”训练样本的正确分类“与”决策函数的边际最大化“两个不可同时完成的目标,希望找出一个平衡点来让模型的效果最佳。
| 参数 | 含义 |
|---|---|
| C | 浮点数,默认1,必须大于等于0,可不填 松弛系数的惩罚项系数。如果C值设定比较大,那SVC可能会选择边际较小的,能够更好地分类所有训练点的决策边界,不过模型的训练时间也会更长。如果C的设定值较小,那SVC会尽量最大化边界,决策功能会更简单,但代价是训练的准确度。换句话说,C在SVM中的影响就像正则化参数对逻辑回归的影响。 |
在实际使用中,C和核函数的相关参数(gamma,degree等等)们搭配,往往是SVM调参的重点。与gamma不同,C没有在对偶函数中出现,并且是明确了调参目标的,所以我们可以明确我们究竟是否需要训练集上的高精确度来调整C的方向。默认情况下C为1,通常来说这都是一个合理的参数。
如果数据很嘈杂,那往往减小C。当然,也可以使用网格搜索或者学习曲线来调整C的值。
#调线性核函数
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
clf = SVC(kernel="linear",C=i,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
#换 rbf
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
clf = SVC(kernel="rbf",C=i,gamma = 0.012742749857031322,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
#进一步细化 5-7
score = []
C_range = np.linspace(5,7,50)
for i in C_range:
clf = SVC(kernel="rbf",C=i,gamma =
0.012742749857031322,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()