数据结构图的实现,优先搜索和迪杰斯特拉算法(单源最短路径),Kruskal算法(最小生成树)的实现
1.图的分类
图分为无权无向图,加权无向图,无权有向图和加权有向图。
我们可以让加权有向图作为超类,其他的图作为他的派生类。
当权值都相同时就相当是无权图了,当凡是有边(i,j)总是有边(j,i)就相当于是无向图了。
为了讨论迪杰斯特拉和Kruskal算法简单,这里我们选用加权无向图。
2.图的实现:
通常图的实现方式有邻接矩阵,邻接链表和邻接数组三种方式。我这选用的邻接矩阵最容易实现。
代码实现如下:
template <class T>
class adjacencyWGraph{
protected:
int n;
int e;
T noEdge;//表示不存在的边的表示方法
public:
T **a;//邻接矩阵
int *reach;//记录是否经历过的数组
int *path_dfs;//记录深度优先搜索的路径
//1.带有默认参数的构造器
adjacencyWGraph(int nV = 0,T theNoEdge =0){
if(nV < 0){
throw "顶点个数必须大于0!";
}
n = nV;
e = 0;
noEdge = theNoEdge;
//创建邻接矩阵
a = new T*[n+1];//数组的数组是二维数组
for (int j = 1; j <=n ; ++j) {
a[j] = new T[n+1];
}
//初始化邻接矩阵
for (int i = 1; i <= n ; ++i) {
for (int j = 1; j <=n ; ++j) {
a[i][j] = noEdge;
}
}
//对reach初始化
reach = new int[n+1];
for (int i = 1; i <= n; ++i) {
reach[i] = 0;
}
//初始化path
path_dfs = new int[n];
for (int k = 0; k < n ; ++k) {
path_dfs[k] = 0;
}
}
~adjacencyWGraph(){
//二维数组的析构方法
for (int i = 1; i <= n; ++i)
{
delete [] a[i];
}
delete [] a;
a = NULL;
delete [] reach;
}
用二维数组a来表示矩阵。在构造函数中对图进行了初始化。reach和path_dfs是记录优先搜索的辅助变量。
其中构造器theNoEdge表示的是(i,j)之间无边有用户给定,一般是一个很大的值。
3.图的一些常规操作
插入边,判断边是否存在,删除边,计算顶点的度
int numberOfVertices() const { return n;}
int numberOfEdges() const { return e;}
bool directed() const { return false;}
bool weighted() const { return true;}
//2.判断(i,j)边是否存在
bool existsEdge(int i,int j) const{
if (i<1||j<1||i>n||j>n||a[i][j] == noEdge){
return false;
} else{
return true;
}
}
//3.插入边 参数是起点终点和权重
void insertEdge(int v1,int v2,T weight){
if(v1<1||v2<1||v1>n||v2>n||v1==v2){
throw "如此插入非法!";
} else{
if (a[v1][v2] == noEdge){
e++;
}
a[v1][v2] = weight;
a[v2][v1] = weight;
}
}
//4.删除边
void easeEdge(int i,int j){
if(existsEdge(i,j)){
a[i][j] = noEdge;
a[j][i] = noEdge;
e--;
}
}
//5.顶点的度
int degree(int theV) const{
int sum = 0;
for (int i = 1; i <=n ; ++i) {
if (a[theV][i] != noEdge){
sum++;
}
}
return sum;
}
4.图的遍历
1)广度优先搜索
类似于完全二叉树的层次遍历完全二叉树的四种遍历方式见这里图的广度优先搜索也要用到队列这种数据结构。搜索原理是从起点i开始,将与i邻接的点全部存入队列,直至i没有邻接的点为止,然后如果队列不为空从队列中取出点,重复上边的操作。
代码如下:
//1.bfs遍历(广度优先搜索 用到队列)
//参数 起始点和标记数字
void bfs(int v,int label){
arrayQueue<int> q(10);
int reach[n+1] ;
for (int i = 1; i <= this->n+1; ++i) {
reach[i] = 0;
}
reach[v] = label;//先将v其实元素标记!
q.push(v);
while (!q.empty()){
int w = q.front();
q.pop();
for (int u = 1; u <= this->n ; ++u) {
//w,u之间有边并且u没有被遍历过
if(this->a[w][u] != this->noEdge&&reach[u] == 0){
q.push(u);
reach[u] = label;
}
}
}
}
2)深度优先搜索
同完全二叉树的前序遍历类似,深度优先搜索也要使用递归的方法。
原理,从起点i开始找到与i邻接的某一点,将该点作为起点重复深度优先搜索,如果该点没有邻接的顶点或者邻接的顶点都被经历过了,则返回。
代码如下:
//2.dfs 深度优先搜索任意起点的
int path_number=0;
void dfs(int v,int label){
path_dfs[path_number] = v;//将路径记录下来
reach[v] = label;
path_number++;
for (int i = 1; i <=n ; ++i) {
if (a[v][i]!=noEdge&&reach[i]==0){
dfs(i,label);
}
}
}
可见深度优先搜索实现非常简单并且不需要借助队列这种数据结构,和我们想的一样,要想获取更高效的图的算法,深度优先搜索使用的更多。
5.迪杰斯特拉算法
在图中我们经常遇到这样的问题,求从i到j的最短路径,这就是单源最短路径问题,解决的一种思路就是迪杰斯特拉算法。
原理:每次从一条最短路径还没有到达的顶点中,选择一个可以产生最短路径的目的顶点。
伪代码:计算并保留图G中原点s到每一顶点v的最短距离d[v],同时找出并保留v在此最短路径上的“前趋”,即沿此路径由s前往v,到达v之前所到达的顶点。其中,函数Extract_Min(Q) 将顶点集合Q中有最小d[u]值的顶点u从Q中删除并返回u。
1 function Dijkstra(G, w, s)
2 for each vertex v in V[G] // 初始化
3 d[v] := infinity // 将各点的已知最短距离先设成无穷大
4 previous[v] := undefined // 各点的已知最短路径上的前趋都未知
5 d[s] := 0 // 因为出发点到出发点间不需移动任何距离,所以可以直接将s到s的最小距离设为0
6 S := empty set
7 Q := set of all vertices
8 while Q is not an empty set // Dijkstra算法主体
9 u := Extract_Min(Q)
10 S.append(u)
11 for each edge outgoing from u as (u,v)
12 if d[v] > d[u] + w(u,v) // 拓展边(u,v)。w(u,v)为从u到v的路径长度。
13 d[v] := d[u] + w(u,v) // 更新路径长度到更小的那个和值。
14 previous[v] := u // 纪录前趋顶点
C++代码实现:
//3.迪杰斯特拉算法
void Dijkstra(int n, int v){
int **c = a;
int dist[n+1];//记录距离
int prev[n+1];//记录前驱
bool s[maxnum]; // 判断是否已存入该点到S集合中
//对距离和前驱进行初始化
for(int i=1; i<=n; ++i)
{
dist[i] = c[v][i];
s[i] = 0; // 初始都未用过该点
if(dist[i] == noEdge)
prev[i] = 0;//与v不邻接
else
prev[i] = v;
}
dist[v] = 0;
s[v] = 1;
// 依次将未放入S集合的结点中,取dist[]最小值的结点,放入结合S中
// 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度
// 注意是从第二个节点开始,第一个为源点
for(int i=1; i<=n; ++i){
int tmp = noEdge;
int u = v;
// 找最短路径
for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]<tmp)
{
u = j; // u保存当前邻接点中距离最小的点的号码
tmp = dist[j];
}
s[u] = 1; // 表示u点已存入S集合中
// 更新dist
for(int j=1; j<=n; ++j)
if((!s[j]) && c[u][j]<noEdge)
{
int newdist = dist[u] + c[u][j];//计算通过新的点到达j能否经过更短的距离
if(newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
for (int k = 1; k <= n ; ++k) {
if (dist[k]==noEdge){
cout<<0;
} else{
cout<<v<<"-"<<k<<":"<<dist[k]<<endl;
}
}
}
关键步骤就是第二个for循环,程序可以完美的输出图的任意顶点的单源最短路径。
6.最小生成树Kruskal算法
基于贪婪策略的最小生成树算法有三种,这里着重介绍第一种,Kruskal算法。
原理:每步选择一条边,这条边的权值最小并且不能与已选择的边构成环路。
结果如图:
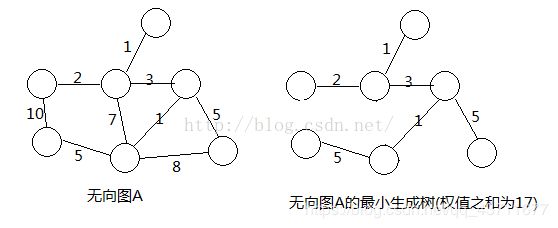
这个问题的难点就是如何区分边能否与已选择的边构成环路,这时我们想到了等价类和并查集,将边的两个顶点作为代表元素,如果这两个顶点不是等价类就合并,如果是等价类就不选择这条边。
并查集没学好的同学请移步大佬的详细讲解。
并查集的实现类
class fastUnionFind{
private:
int n;//节点数目
int *node; //每个节点
int *rank; //树的高度
public:
//初始化n个节点
void Init(int n){
for(int i = 0; i < n; i++){
node[i] = i;
rank[i] = 0;
}
}
//构造函数
fastUnionFind(int n) : n(n) {
node = new int[n];
rank = new int[n];
Init(n);
}
//析构函数
~fastUnionFind(){
delete [] node;
delete [] rank;
}
//查找当前元素所在树的根节点(代表元素)
int find(int x){
if(x == node[x])
return x;
return node[x] = find(node[x]); //在第一次查找时,将节点直连到根节点
}
//合并元素x, y所处的集合
void unite(int x, int y){
//查找到x,y的根节点
x = find(x);
y = find(y);
if(x == y)
return ;
//判断两棵树的高度,然后在决定谁为子树
if(rank[x] < rank[y]){
node[x] = y;
}else{
node[y] = x;
if(rank[x] == rank[y]) rank[x]++;
}
}
//判断x,y是属于同一个集合
bool same(int x, int y){
return find(x) == find(y);
}
};
图边的实现类:
为了实现方便我已重载了运算符==和输出流“<<”
class Edges{
public:
int start;
int end;
int weight;
//运算符的重载
bool operator == (const Edges& b)
{
return ((b.start==this->start)&&(b.end==this->end)&&(b.weight==this->weight));
}
//输出符号的重载
friend ostream &operator<< (std::ostream&, const Edges&);
};
ostream &operator << (ostream& os, const Edges& e)
{
os << e.start<<"-"<<e.end<<":"<<e.weight<<endl;
return os;
}
算法实现:
//4.Ktuskal算法 计算最小生成树
bool kruskal(Edges spanning[]){
int n = this->n;
int e = this->e;
//边集合E
Edges edges[e];
//对边集合E初始化
int k = 0;
for (int i = 1; i <= n ; ++i) {
for (int j = 1; j <= n ; ++j) {
if(existsEdge(i,j)&&i<j){
edges[k].start = i;
edges[k].end = j;
edges[k].weight = a[i][j];
k++;
}
}
}
//并查集问题!
fastUnionFind uf(n+1);
k =0;
while (e>0&&k<n-1){
Edges x = min_from(edges,this->numberOfEdges());
e--;
int a = x.start;
int b = x.end;
if(uf.find(a) != uf.find(b)){//!!!!!!!!!!!!!!!!!!!判断新加入的边是否成环
//加入生成树中
spanning[k++] = x;
uf.unite(a,b);
}
}
return (k == n-1);
}
**while (e>0&&k 辅助方法min_from pEdges[index].weight = 10000;//相当于删除最小的边粗样式这一行就对应着从边集中删除最短的边。 //最小生成树的辅助方法
Edges min_from(Edges pEdges[],int bianshu) {
Edges temp = pEdges[0];
int index = 0;
for (int i = 1; i < bianshu; ++i) {
if (pEdges[i].weight<temp.weight){
temp = pEdges[i];
index = i;
}
}
pEdges[index].weight = 10000;//相当于删除最小的边
return temp;
}