tf.nn.conv2d() / tf.nn.depthwise_conv2d() 和 Batchsize效益

1. 卷积函数tf.nn.conv2d() 

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=True, 
             data_format='NHWC',dilations=[1, 1, 1, 1], name=None)

对于给定的4-D张量输入，利用给定的filter执行2-D卷积运算。

• input : [batch, in_height, in_width, in_channels]
• filter : [filter_height, filter_width, in_channels, out_channels]
• padding: "SAME" / "VALID"
• data_format: Defaults to "NHWC".

算法执行过程：
1.filter压平成2D矩阵，[filter_height * filter_width * in_channels, output_channels]
2.input中提取图像块， [batch, out_height, out_width, filter_height * filter_width * in_channels]
3.对于每一个图像块，右乘滤波器矩阵和图像块向量。

实例：

    

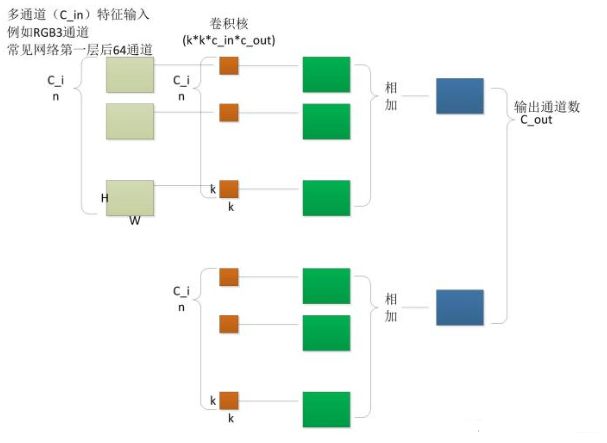
左边代表input：[BatchSize, H, W, in_Channels]=[24,255,255,3];

右侧代表filter：Batch_size*[Filter_H, Filter_W, in_Channels, out_Channels]=[127,127,3,1]; 

所以，程序循环24次，即可以完成对一个BatchSize=24的卷积/相关操作，输出结果为：

这个过程是比较复杂的，Tensorflow中提供了更好的深度卷积deep_wise_conv2d()函数可以执行类似的功能。

2. 深度卷积tf.nn.depthwise_conv2d()

深度卷积最早出现在Google的Xception系列的文章，具体的算法实现可以参考xf_mao博主的这边文章：https://blog.csdn.net/mao_xiao_feng/article/details/78003476。这里我仅仅应用该函数实现了BatchSize图像的对应(Channel-Wise)卷积工作。

tf.nn.depthwise_conv2d(input, filter, strides, padding, rate=None, name=None, data_format=None)

给定4D的输入张量input=[batch, in_height, in_width, in_channels]，滤波器filter=[filter_height, filter_width, in_channels, channel_multiplier]。 该滤波器包括深度为1的in_channels个卷积滤波器。depthwise_conv2d()对每个输入通道(从1到channel_multiplier通道)施加一个不同的filter。然后将输出结果concatenate到一起。输出的通道数=[in_channels * channel_multiplier]。

对照我们的任务。input：[BatchSize, H, W, in_Channels]=[24,255,255,3]; filter：Batch_size*[Filter_H, Filter_W, in_Channels, out_Channels] = [127,127,3,1]; 如果想实现对应图层采用对应核图像进行卷积[Channel-Wise]，我们需要将input和filter的shape进行调整。具体为 input=[1, H, W, BatchSize*in_Channels]; filter=[Filter_H, Filter_W, Batch_Size*in_Channels,1].

核心代码：

Bz, Hz, Wz, Cz = z.shape
Bx, Hx, Wx, Cx = x.shape; 
zf = tf.reshape(zf, (Hz, Wz, Bz*Cz, 1))
xf = tf.reshape(xf, (1, Hx, Wx, Bx*Cx))
print("zf= ", zf.get_shape().as_list(), "    ", "xf=", xf.get_shape().as_list())
    
res_ = tf.nn.depthwise_conv2d(xf, zf, strides=[1,1,1,1], padding='VALID')
res_ = tf.concat(tf.split(res_, 24, axis=3), axis=0)
res_ = tf.reduce_mean(res_, axis=3, keep_dims = False)
print("the results of deep_wise_conv2d:", res_.get_shape().as_list())

输出结果和循环tf.nn.conv2d()的结果一致。

3. 关于mini-batch的作用

3.1 为什么需要有 Batch_Size 这个参数? 

• 合理的范围，越大的 batch size 使下降方向越准确，震荡越小
• batch size 过大，各batch梯度修正值可能消失，出现取得局部最优的情况
• bath size 过小，引入的随机性更大，难以达到收敛，极少数情况下可能会效果变好

Batch的选择决定了优化函数梯度的下降方向。如果数据集比较小，完全可以采用全数据集 ( Full Batch Learning )的形式，这样做至少有 2 个好处：

• 由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向
• 由于不同权重的梯度值差别巨大，因此选取一个全局的学习率很困难。Full Batch Learning 可以使用Rprop只基于梯度符号并且针对性单独更新各权值。

对于类似于ImageNet等超大数据集，以上 2 个好处又变成了 2 个坏处：

• 随着数据集的海量增长和内存限制,一次性载入所有的数据进来变得越来越不可行
• 以 Rprop 方式迭代，由于各个 Batch 间的采样差异，各次梯度修正值相互抵消，这才有了后来RMSProp的妥协

如果每次只训练一个样本,即 Batch_Size = 1。这就是在线学习(Online Learning)。线性神经元在均方误差代价函数的错误面是一个抛物面,横截面是椭圆。对于多层神经元、非线性网络,在局部依然近似是抛物面。使用在线学习,每次修正方向以各自样本的梯度方向修正,横冲直撞各自为政,难以达到收敛。如上图所示。

3.2 Mini-Batch 可以解决什么问题？

如果数据集足够充分,那么用一半(甚至少得多)的数据训练算出来的梯度与用全部数据训练出来的梯度是几乎一样的。这就是批梯度下降法(Mini-batches Learning)。

在合理范围内,增大 Batch_Size 有何好处?内存利用率提高了,大矩阵乘法的并行化效率提高。 跑完一次 epoch(全数据集)所需的迭代次数减少,对于相同数据量的处理速度进一步加快。 在一定范围内,一般来说 Batch_Size 越大,其确定的下降方向越准,引起训练震荡越小。 盲目增大 Batch_Size 有何坏处?内存利用率提高了,但是内存容量可能撑不住了。 跑完一次 epoch(全数据集)所需的迭代次数减少,要想达到相同的精度,其所花费的时间大大增加了,从而对参数的修正也就显得更加缓慢。 

3.3 调节 Batch_Size 对训练效果影响到底如何? 

Batch_Size 增大到一定程度,其确定的下降方向已经基本不再变化。 调节 Batch_Size 对训练效果影响到底如何? 这里展示了在 MNIST 数据集上的效果。如图所示:

算法架构：

 

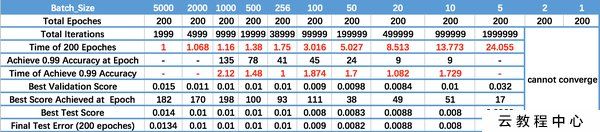
Batch_Size对训练结果的影响：

结论：

• Batch_Size 太小,算法在 200 epoches 内不收敛。 
• 随着 Batch_Size 增大,处理相同数据量的速度越快。 
• 随着 Batch_Size 增大,达到相同精度所需要的 epoch 数量越来越多。 
• 由于上述两种因素的矛盾, Batch_Size 增大到某个时候,达到时间上的最优。 由于最终收敛精度会陷入不同的局部极值,因此 Batch_Size 增大到某些时候,达到最终收敛精度上的最优。