2019年上海市数学建模讲座笔记(1)竞赛真题讲解
《竞赛真题》
2018年国赛A题讲解:《数学建模及其应用》杂志,第一期,复旦大学蔡志杰老师
关于选题
竞赛规则的变化
开始时间:礼拜四,9.12晚上6点开始。下载题目
去年40000多个队伍,
两个文件的码上传,星期五的晚上,需要匹配。生成码之后不要修改,做一个备份。
提交时间:不要在10点钟后上传,截止时间是15号八点。最晚9:30上传。
选题:
本科组 ABC三个题
评奖规则变化:
去年5分一等奖,10个二等奖。
今年是6+6,按照题目分配,每个题目4个
选题需要注意:不要选择太容易的,校内就pk掉了,可能失去评优的资格。
有一条:不允许公开选的题目,不能校内公开讨论。
B题题目难懂。A题读题简单,结果:模型结果算不出来。
150个一等奖,
A题60%获奖率
B题获奖率80%
题目需要有想法,太平淡没有特色。
选题:不能选没有完全没有想法的题目。
以上是关于选题的问题。
《高温作业专用服装设计》
复旦大学 蔡志杰
以下是听课笔记:包括部分照片,如有侵权,请联系删除。该博客请不要用于商业用途,仅供学习参考使用。当然,这是笔者学习的笔记记录。
去年的A题
热量传递模型
问题重述:
防热服,参数设置,三层
存在第四层:空气层衣服和皮肤之间
测量假人皮肤温度
问题一
计算温度分布。
考虑:温度和什么因素有关
生成电脑文件,文件名,格式等需要注意。
数据1:参数:密度,比热,热传导率,厚度,给定(数据来源:公开资料)
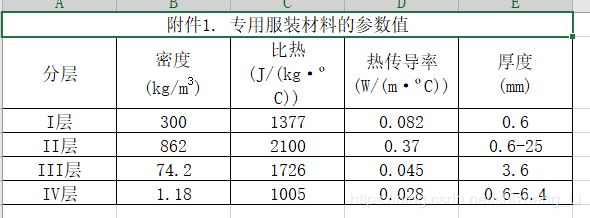
两个值厚度第二层和第四层给定范围。需要自己给出最佳厚度
数据2:测量数据,皮肤温度(数据来源:竞赛公开资料)
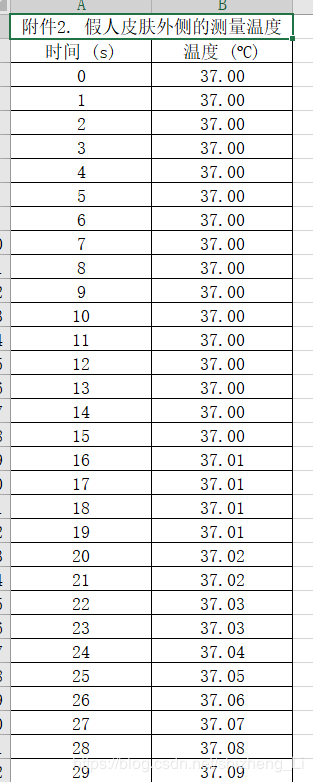
阅卷的时候:很多人数据插值拟合,这个数据不是这么用的。
老师忠告:涉及一个时候插值拟合的问题,需要知道做这个的目的,有用的话才要做。
问题2:
确定第二层的最有厚度 ,两个条件:皮肤外侧温度不能超过四十七度,还有时间问题
问题三:确定两层的最优厚度
第二板块:热量传递模型
三维问题,厚度很薄,转化为一维问题
两维半:圆柱体 也可以
简化:一维问题
建系:高温环境和衣服作为坐标原点,朝向人为x轴
模型的建立:
微元法
三维 热量守恒定律,现在是一维的,跟y,z有关的项去掉
热传导微分方程的建立;
比热,密度,k热传导系数
偏微分方程 ,扩散方程,热传导
书上一般不会讲多层介质,需要进行形式变化,每一层需要分别建立模型
得到的是一个方程组
注意:不包括五个点,边界和层和层的交界点
补充条件进去
问题难点:不在于建模型本身,关键问题在于:定解条件
任意常数,确定需要条件
常微分方程:
偏微分方程有任意函数
确定任意函数两类条件:初始条件,假人的温度可控u0可设置
更复杂的条件:边界条件
一般有三类边界条件:竞赛的模型错了,边界条件的选择错了 80%的队伍
热量和服装进行热交换:热量传递的边界条件:
牛顿冷却定律,傅里叶热传导定律
给我的思考是什么:确定理论,查找资料,需要钻进去,用三天的时间学习一个知识,需要特别注意使用的条件,知识的变异用法。
现在确定外法线方向 区间左端点外法线方向是-x方向
需要注意符号,下标e是环境的意思
思考:需要数学公式的编写,软件需要下载(这方面能力我还是欠缺的)
如果模型是对的,需要注意符号,这里是对公式的理解
还有一个难的地方:
五个点没有方程:交界点
过渡信息没有,额外给出来
称之为交界面条件,
思考:跟应用偏微分方程有关的书籍才会讲到,大多数是不讲的,查资料的时候需要多找
建模最难的地方:交界面条件,书上没有
两个:每个都缺少一定信息,需要组合起来
第一个:温度连续u-等于u+
很多同学认为i:导数连续
但是不对
热传导率不相等,乘以k之后连续
左边传过去 的热量等于右边的热量
比较完整的模型
第三部分计算方法
程序不好的话,半个小时算不出来
方法:有限差分法:差商代替导数,微分方程用
导数的定义,一个极限
可以去掉极限符号,称之为差商,一阶向前差商
时间方向前面的值
另外的形式
h变为负号也可以:一阶向后差商
需要用上面的两个形式
h为步长
两阶导数:一阶导数的一阶导数
一阶差商的一阶差商
一阶向前差商的一阶向后差商
整理之后得到 二阶差商
空间,时间有关,两阶,偏导数,差商近似
其他所有自变量给定,只有一个变量在变
得到关于x的偏导数一阶差商:y是固定的
同样可以求关于y的差商
关于时间用一阶差商
关于空间需要两阶差商
两种可能:向前或者向后,两种形式原则上都是可以的
具体怎么处理
第一步,确定步长,时间步长和空间步长
时间:delta,等分,
空间步长 每个区间不一样,区间等分,
可以求坐标
向后差商
两阶差商
得到方程,相等得到,对于方程的差分格式
方程组,线性方程组
高斯消去法求解
n这个时间的所有点温度想要知道的
需要知道n-1
递推公式
模型需要知道初始条件
算的时候
是一个循环,关于时间的循环
假设5400s,
循环体是解决方程组
方程的问题:无穷多解
左边没有东西,对内点成立
补充条件:五个点
边界条件:左边边界:
一阶向前差商
右边边界:一阶向后差商
补充上两个方程已经
再补充
交界点需要补充
温度连续:隐含着用掉了
到这里:方程个数和变量个数相等了,方程可解
问题:方程的阶数很高
用到吸收矩阵的方式,求解方程
计算时间4s,优化的算法,一次计算
还要考虑方程的特点,可以优化
Ax=b
方程组:三对角线性方程组
用的是追赶法来处理的
A=LU
A是一个矩阵
L是下三角 U是上三角
其中一个矩阵对角线全部是1,单位三角矩阵
右边两个矩阵相乘,对应左边的矩阵的对应位置的元素
矩阵结合律,
两次来求解
最大的好处:每一个变量都可以直接做出来
没有听清y是什么,这里用了换元法
后面算u用的是从后往前算
ly=b
求y1,然后地推求yi
求x
ux=y
矩阵分解,两次的矩阵方程组,若干次循环可以做掉
高斯消去法 时间复杂度n3
追赶法:时间复杂度 On
不同的线性方程组,选择不同的计算方法
怎么看温度关于空间的单调性
x和t互换一下画图
固定一个时间,看单调性
需要对结果的分析,用数据进行分析,把单调性表达出来
老师:因为主观上好理解,很多队伍没有给出来单调性。
温度单调性的图
第四部分:稳态模型
这里略讲
没有时间t
为什么用这个模型
对于一维情况,存在解析解
需要用公式解对结果进行检验
得到绝对误差
这个题目有陷阱
第五部分:热交换系数的确定
ke和ks
没有提到这两个参数的存在
难度在这里,东西没告诉
问题:确定最佳参数,使得解出来的结果和方程测量值尽可能接近
平方误差最小
怎么计算呢?
最速下降法,牛顿法
穷举法:离散化,每一个离散点选择最优的
变步长的枚举
找到最优解然后加密,在附近继续寻找
使用条件:两个变量可以用,三个变量是极限,4个绝对不能用
随着变量的个数指数增长
反过来:如果变量可以减少的话,可以用穷举法,计算量大大减少
借用稳态模型,减少变量个数
给出了每一个点的温度
利用稳态模型公式得到ks和ke的关系,用ke标识ks
只有一个变量了现在
问题转变成为只有一个优化变量的优化问题
第一个问题解决了,现在。
第二个问题
第六部分:第二层厚度的最优设计
关键点:写出来模型
优化问题,目标
还有约束条件
s.t T=5400s给出的终止时间
只要这一个点,利用单调性
下面 超过44度时间不能超过300s
积分,对1积分,积分区域,大于等于44度这个约束条件,不是显示条件
离散化,1s算一次
总的累加不超过300s
计算量也是有的
可以变成一个简单的条件:
在结束时候之前300s不超过44度:利用的是单调性
思考:好好利用单调性,多做一些东西,可以产生很好的优化
还需要另外一个单调性
皮肤外侧温度和厚度单调递减
用两分法来做
log2n 复杂度
计算一次十几秒
记号:第二层厚度d2
思路完整性用思维导图来分类思考
找中点
两种情况
满足约束,不满足条件
算法结束:dmax-dmin《伊普瑟隆
第七部分:多目标优化
第三个问题:
两层都不知道厚度
模型难度转化,转化为多目标优化问题
思路:转化为单目标问题,找一个折中方案
加权平均是多数同学用的方法
更多是是阿利法去0.5,但是是没有理论依据的,是凭空猜测的
相对好的取到 密度,重量最小,这个加权有理由
思考:选取需要结合题目,对结果进一步分析
温度和厚度单调递减
第四层厚度和第二层厚度负相关
最薄,只能一个厚一点,一个薄一点,存在一个优先级的问题,这是另外一个解法
这个问题的优先级呢?第二层需要薄,第四层是空气,可以厚一点
结合实际情况,
直接取到第四层最厚,第二层最薄
这种方法用这样来做。
第八部分,讲评
1.边界条件
第一类边界条件
不是系统
第二类
不能用,没有偏导数的值
等于零是绝热条件,不传递
使用的是第三类边界条件
2差分格式
向后,隐式格式
向后差商是显示格式,显式格式:条件稳定 拉姆达小于二分之一
只能用隐式格式来做,无条件稳定
3解析解
分离变量法
傅里叶变换都不能用:有界限区间,不能用
4检验
热交换系数未知
通过计算得到,存在误差
误差有影响吗影响多大
检验
方法:对测量值加上随机误差,得到新的交换系数,通过第二问第三问做最优设计,比较,考察是否有很大变化
检验
参数的影响 比如0-1 变化看影响
微小变化有什么变化
至少要做一个检验。
【总结一下】
1.复旦大学蔡志杰老师讲解的深入浅出,数学思想的讲解收获很大。
2.以2018年A题为例,讲解了整个建模的过程,是如何进行思考的,遇到这个问题应该怎么办,遇到那个问题应该怎样解决。一步一步有理有据,论据充分,这是我们需要着重学习的。
3.关于知识点。
微分方程,解的情况,边界条件,如何求解:分离变量,傅里叶变换等等不一定有用
差分格式:向前差分,向后差分
参数检验:不是所有的数据都要用,留下几组用来检验。
多目标规划:注意加权平均数使用
求单调性:用二分法,时间复杂度logn
确定最佳参数,使得解出来的结果和方程测量值尽可能接近:
高阶矩阵的计算:考虑矩阵的特点,使用追赶法来处理。
备注:笔记需要结合优秀论文来看。
写作这篇博客的目的:把上课的知识进行复习,进行查漏补缺,复习提高相应的方法,相应的知识。




