支持向量机（SVM）——斯坦福CS229机器学习个人总结（三）

鉴于我刚开始学习支持向量机（Support vector machines，简称SVM）时的一脸懵逼，我认为有必要先给出一些SVM的定义。

下面是一个最简单的SVM：

图一

• 分类算法：支持向量机（SVM）是一个分类算法（机器学习中经常把算法称为一个“机器”），它的目标是找到图中实线所表示的决策边界，也称为超平面（Hyperplane）
• 支持向量（Support vectors）：支持向量就是图中虚线穿过的数据点（两个×与一个O），直观上来看，它们确定了超平面的位置——超平面与过同一类的两个支持向量（两个×）的直线平行，并且两类支持向量到超平面的距离相等
• 与logistic回归的对比：SVM与logistic回归用的是相同的模型，但是处理方式不一样——logistic回归用概率的方式求解模型（最大似然估计），SVM从几何的角度解析；另外在logistic回归中，每一个数据点都会对分类平面产生影响，在SVM中它却只关注支持向量（如果支持向量无变化，增加或者删除一些远处的数据点，产生的超平面还是一样的）——所以产生了这两个不同的算法，但是它们还是比较相似的

明明是SVM算法却在这里提到logistic回归模型是为了作为源头引出SVM的推导，至于更深的背景，比如SVM被认为几乎是最好的监督学习啦，SVM是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的啦，SVM作为统计机器学习与传统机器学习的本质区别啦……目前的我还没有形成一个整体的、完善的认识，虽然下一份总结里就要说到学习理论与结构风险最小化，但是对于海面之下的冰山，我暂时还没法看到。在这里我只是想老老实实地把SVM从推导，到转换与优化，到最后求解的过程做一个总结写下来。

还需要说明的是，图一是最简单的SVM，它是线性可分的，并且从图一上来看它是没有噪点的，第一章“SVM的推导”可以把这个漂亮的线性可分的模型推导出来。
但是实际的情况不可能这么完美。当数据线性不可分的时候，我们需要引入核函数在更高维的空间里去寻找这个超平面（数据在更高维的空间里会更加线性可分）；当噪点存在的时候，我们引入软间隔分类器，这时候在支持向量附近，允许有一些噪点被分错，即允许误差的存在。而这两点都是在将目标函数转化为对偶问题之后实现的。这些都会在第二章“SVM转换与优化”中介绍。

1、SVM的推导

1.1、起源

SVM与logistic回归使用了相同的模型，现在让我们来回顾一下熟悉的logistic回归模型：

hθ(x)=g(θTx)=11+e−θTx(1)

其中：

g(z)=11+e−z(2)

并且其图像如下图：

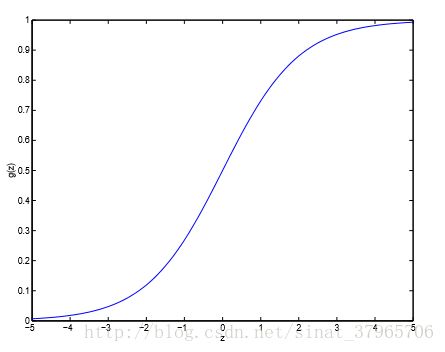
图二
图像的输出是“分类结果 g(z) 是1的 概率”，它的取值范围是 (0,1) ，一般来说以0.5为界，当 g(z) 是1的概率大于0.5的时候，把 x 分类为1，当 g(z) 是1的概率小于0.5的时候，把 x 分类为0，这样，虽然它的直接输出是 (0,1) 之间的概率，却有感知器那样的分类效果。
同时可以看到当 z 在0附近时，输出概率在0.5附件徘徊，而且比较敏感，但是当 z=θTx>>0 时它的输出很接近1，当 z=θTx<<0 时它的输出很接近0。所以如果我们能够让 z>>0 或者 z<<0 ，我们就会更加确信这个样本被正确分类了。
换句话说，如果把 z=0 这条直线当做决策边界，那么数据点 z 距离这条直线越远，就越不可能被分错。
SVM就是从几何的角度，在这方面下功夫的。

下面是在logistic回归模型下，因为SVM这个算法的特点而引起的符号改变：

y=hθ(x)=g(θTx)=g(wTx+b)=hw,b(x)(3)

直观点的改变是：

θTx=θ0+θ1x1+θ2x2+⋯+θnxn=b+w1x1+w2x2+⋯+wnxn=wTx+b(4)

截距b就是截距 θ0 ，向量 w 就是除了 θ0 外，剩下的向量 θ ，而且这里的向量 x 应该是差了一个 x0=1 （ xθ,θ∈Rn+1 ， xw,w∈Rn ），但是不影响…它们表达的意思是一样的，只是换了些符号而已。
另外，这里的 g(z) 不再是式（2）中的形式，而是：

g(z)={1−1if(z≥0)if(z<0)(5)

恩…长得很像感知器。
式（3）与式（5）就是SVM模型了，参数是 θ 与 b ，当这两个参数确定了，我们就可以做出分类超平面，对数据进行分类。

对同一个模型，logistic模型用概率的方式求解，下面就要引入函数间隔与几何间隔来从几何的角度来解析SVM了。

1.2、函数间隔（Functional margins）与几何间隔（Geometric margins）

给定一个训练样本 (x(i),y(i)) ，我们将其函数间隔定义为：

γ^(i)=y(i)(wTx(i)+b)(6)

函数间隔的作用有两个。
一个是 确认样本点有没有被正确分类：
由式（3）与式（5）可以知道， y(i) 的取值为{ 1,−1 }，那么在 w,b 确定了，并且样本被正确分类的情况下， wTx+b 与 y(i) 是同号的，即 γ^(i)=∣∣(wTx+b)∣∣ ，所以当函数间隔 γ^(i)>0 ，即 γ^(i) 是正数的时候，我们就认为这个点被正确地分类了（错误分类时 γ^(i)<0 ）。
另一个是 衡量该样本点被正确分类的确信度：
在起源中由sigmoid函数 g(z) 我们注意到，一个点离超平面越远，其输出就越接近1，同样地， γ^(i) 越大，这个样本被分对的也确信度越大。

进一步地，相比只有一个训练样本的情况，如果给定一个训练集 S= { (x(i),y(i);i=1,2,⋯,m) }，那么整个训练集合的函数间隔为：

γ^=mini=1,2,⋯,mγ^(i)(7)

有了函数间隔我们就可以去选择超平面了，在判断数据点有没有被正确分类这一点上，函数间隔没有问题。当所有样本点的函数间隔都是正数的时候，它们就全都被正确分类了（在这里讨论的是数据集线性可分的情况，如图一所示）。
需要注意的是，此时的超平面不一定就是最优的，所以我们还要最大化其被分类正确的确信度，这时候就需要依赖到函数间隔的第二个作用了。

但是在使得确信度最大这一点上，函数间隔却存在着缺陷。我们希望在样本点全部被正确分类的前提下，它们被分对的确信度最大，即让 γ^ 尽可能地大（这与式（7）中选取最小（即确信度最小）的 γ^(i) 来作为整个训练集的函数间隔 γ^ 并不矛盾，还有点在确立最大下界的意思）。
可是我们发现，只要成比例地改变 w 与 b ，比如把它们变成 2w 与 2b ，超平面并没有发生改变，但是函数间隔 γ^ 却变成了原来的两倍，这意味着，我们可以成比例地增大 w 与 b ，使得函数间隔 γ^ 变得无限大。这显然没有意义，因为超平面的位置并没有发生改变。

这时候就轮到几何间隔出场了，它是增加了约束的函数间隔，使函数间隔变得唯一，用符号 γ 表示。
直观上来看几何间隔是样本点到超平面的距离。
此时改变几何间隔就能够移动超平面，同时几何间隔仍然能反映样本被正确分类的确信度，所以对几何间隔的最大化，就是对超平面的最优化。

下面我们借助图三来寻找几何间隔：

图三
设点B是向量 x ，点B在超平面上，点A为样本点向量 x(i) 。
因为点A与点B在法向量 w 上的距离就是几何间隔 γ(i) ，所以我们有：

x(i)−γ(i)w∥w∥=x(8)

因为 γ(i) 只是一个距离常量，所以需要乘上法向量 w 的单位向量 w∥w∥ （ ∥w∥ 是向量 w 的长度， ∥w∥=w21+w22+w23+⋯+w2n+−−−−−−−−−−−−−−−−−−−−−√ ），才能在向量间直接做加减。
因为点B在超平面上，所以我们有：

wTx+b=wT(x(i)−γ(i)w∥w∥)+b=0(9)

对式（9）进行求解即可得到几何间隔的形式化定义：

γ(i)=wTx(i)+b∥w∥=(w∥w∥)Tx(i)+b∥w∥(10)

这是样本点在正侧的情形，如果样本点在负的一侧，那就是：

γ(i)=−((w∥w∥)Tx(i)+b∥w∥)(11)

所以为使公式一般化，几何间隔如下表示：

γ(i)=y(i)((w∥w∥)Tx(i)+b∥w∥)(12)

几何间隔与函数间隔的关系是：

γ(i)=γ^(i)∥w∥(13)

所以说几何间隔是增加了约束的函数间隔，是对函数间隔的完善，这时如果成比例地改变 w 与 b ，几何间隔是不会改变的。

类似地，相比只有一个训练样本的情况，如果给定一个训练集 S= { (x(i),y(i);i=1,2,⋯,m) }，那么整个训练集合的几何间隔为：

γ=mini=1,2,⋯,mγ(i)(14)

1.3、最优间隔分类器（The optimal margin classifier）

有了几何间隔，我们就可以确定最优超平面的位置，即最优间隔分类器了：

maxγ,w,bγs.t.y(i)((w∥w∥)Tx(i)+b∥w∥)≥γ,i=1,2,⋯,m(15)

把图一再贴上来一次，并且默认上方的叉叉为正实例，下方的圈圈为负实例：

为什么说满足了式（15）的超平面就是最优间隔分类器，即图中的实线？
首先，在 正确分类的情况下，我们要承认 几何间隔 γ 是正数（如果 γ 是负数，证明分类都不正确，那就没有讨论下去的必要了，更不用提什么最优），所以如果每个样本点都服从了式（15）中 y(i)((w∥w∥)Tx(i)+b∥w∥)≥γ 这个式子，那么我们就可以认为“所有样本点的几何间隔都大于一个正数”，即这些样本点都被正确分类了。这正是函数间隔的第一个作用。于是在这个前提下，我们发现超平面只能画在图一的两条虚线即支持向量之间，而且要跟虚线平行。

其次，我们来考虑最优的问题。虽说确定了超平面一定在两条虚线之间，但是那里面仍然有无数个超平面，如何确定最优？
综合几何间隔与函数间隔的第二个作用，我们有这样的结论：“几何间隔越大，样本被正确分类的确信度越大”，当式（15）中 maxγ,w,bγ 这个式子满足的时候，我们发现超平面正好处于两条虚线的中线位置，它也是我们直观上能想象到的最好的位置了。为什么这么巧？
直观上来说，支持向量是最靠近超平面的存在，所以由式（14）可以知道，支持向量的几何间隔，就是整个样本集的几何间隔，因为其它的点离超平面更远，不在考虑范围之内了。
我们可以想象一下这条实线（超平面）沿着平行的方向上下移动，举个极端的例子，超平面移动到支持向量上，与某一条虚线重合了，这时候所有样本点也是分类正确的，但是此时的几何间隔 γ=0 ，它是不满足“几何间隔最大”这个要求的，然后我们慢慢将超平面从虚线向另一侧的虚线移动，每移动一分几何间隔 γ 就增大一分，直到达到中线的位置，支持向量到超平面的距离相等， γ 才达到最大，超平面达到最优（如果超平面继续向另一侧虚线移动， γ 又会变小）。

解释了这么多是为了说明，满足了式（15）的参数 w,b 可以确定最优超平面，所以它就是我们的目标函数了。那是不是就可以开始对式（15）进行求解了，求解得到了 w,b ，SVM的工作就完成了。

嗯，是的，求解得到 w,b ，SVM的工作就完成了。但是，工作还没有开始。因为这个样子的目标函数没法求解，或者直接求解难度太大，因为它不是一个凸函数，没法用常规的梯度下降或者牛顿法求解。目前的我也不知道如果不用讲义上给的方法，还有没有别的方法可以手动求解。所以，按着给出的方法接着往下走吧。

由函数间隔与几何间隔的关系 γ(i)=γ^(i)∥w∥ ，我们可以对 式（15）进行如下的改写：

maxγ^,w,bγ^∥w∥s.t.y(i)(wTx(i)+b)≥γ^,i=1,2,⋯,m(16)

因为函数间隔的改变不影响超平面的位置，所以为了进一步化简目标函数，我们给函数间隔一个约束 γ^=1 使其变得唯一，此时 γ^∥w∥=1∥w∥ ，又因为最大化 1∥w∥ 与最小化 12∥w∥2 是一样的，所以有：

minγ,w,b12∥w∥2subject toy(i)(wTx(i)+b)≥1,i=1,2,⋯,m(17)

这样，目标函数就变成式（17）的样子了，接下来就可以对这个函数进行求解了。

2、SVM的转换与优化

2.1、SVM转换——引入拉格朗日对偶与KKT条件

2.1.1、目标函数转化为原始问题（Primal problem）

现在，我们将目标函数式（17）改写一下 ：

令f(w)令g(wi)=12∥w∥2=−y(i)(wTx(i)+b)+1≤0(18)

然后引入 拉格朗日乘子（Lagrange multipliers） αi≥0(i=1,2,⋯,n) 得到如下 原始问题：

minw,bmaxα≥0(12∥w∥2−∑i=1mαi[y(i)(wTx(i)+b)−1])=minw,bmaxα≥0(f(w)+∑i=1mαig(wi))=minw,bmaxα≥0L(w,b,α)=minw,bθp(w)(19)

下标 p 被称为原始问题，即：

θp(w)=maxα≥0L(w,b,α)=maxα≥0(f(w)+∑i=1mαig(wi))=maxα≥0(12∥w∥2−∑i=1mαi[y(i)(wTx(i)+b)−1])(20)

虽然很突兀，式（19）与式（17）是等价的。这是因为有被称为 栅栏（Barrier）的带有拉格朗日乘子的那个加项 maxα≥0∑mi=1αig(wi) 的存在，它的作用是将不可行域的 w 排除掉，只留下了可行域内的 w ，式（19）与式（17）一样，都表达了“在 y(i)(wTx(i)+b)≥1(即g(wi)=≤0) 的约束下，对 12∥w∥2(即f(w))求最小值 ”的意思。
我们先来考虑 不可行域的情况。
不可行域指的是不满足约束 y(i)(wTx(i)+b)≥1 的 w ，此时 y(i)(wTx(i)+b)<1 ，即 g(wi)>0 。然后我们看向 maxα≥0∑mi=1αig(wi) 这个加项，因为 α≥0 且 g(wi)>0 ，所以此时求最大值是没有意义的，它的最大值就是无限大。
再来考虑 可行域的情况。
可行域就是 y(i)(wTx(i)+b)≥1 这个区域，此时 g(wi)≤0 。同样地，对 ∑mi=1αig(wi) 求最大值，此时的条件是 α≥0 且 g(wi)≤0 ，明显地，最大值为0。
所以在可行域下有：

θp(w)=maxα≥0(f(w)+∑i=1mαig(wi))=maxα≥0f(w)+maxα≥0∑i=1mαig(wi)=maxα≥0f(w)+0=f(w)(21)

结合起来就是：

θp(w)={f(w)∞w满足原始约束其他(22)

所以引入了拉格朗日乘子的原始问题式（19） minw,bθp(w) 与目标函数式（17）是等价的：

minθp(w)=⎧⎩⎨min12∥w∥2无意义满足y(i)(wTx(i)+b)≥1其他(23)

2.1.2、原始问题与对偶问题（Dual problem）的关系

对于原始问题有：

minw,bθp(w,b)θp(w,b)=minw,bmaxα≥0L(w,b,α)=maxα≥0L(w,b,α)(24)

下标 D 被称为对偶问题，在上式中将 minw,b 与 maxα≥0 的顺序交换一下就变成了对偶问题：

maxα≥0θD(α)θD(α)=maxα≥0minw,bL(w,b,α)=minw,bL(w,b,α)(25)

弱对偶性（Weak duality）

对于一对原始问题与对偶问题，如果它们都存在最优解，并且分别将其表示为 p∗=minw,bθp(w,b) 与 d∗=maxα≥0θD(α) ，那么它们必定有如下关系：

d∗≤p∗(26)

这被称为弱对偶性。有如下证明：

θD(α)=minw,bL(w,b,α)≤L(w,b,α)⟹θD(α)≤maxα≥0L(w,b,α)=θp(w,b)≤θp(w,b)(27)

也可以这么理解：

maxy∈{0,1}(minx∈{0,1}I{x=y})0≤minx∈{0,1}(maxy∈{0,1}I{x=y})1

因为它们都有最优解，所以有：

d∗=maxα≥0θD(α)⟹d∗≤minw,bθp(w,b)=p∗≤p∗(28)

强对偶性（Strong duality）

对于一对原始问题与对偶问题， w∗,b∗ 是原始问题的解， α∗ 是对偶问题的解，并且它们满足KKT条件，有 d∗=p∗ 。这被称为强对偶性，此时可以通过求解对偶问题得到原始问题的解。
KKT条件如下：

拉格朗日平稳(Stationarity):∇wiL(w∗,b∗,α∗)∇biL(w∗,b∗,α∗)=0,i=1,2,⋯,n=0,i=1,2,⋯,l(29)

互补松弛(Complementary slackness):α∗igi(w∗)=0,i=1,2,⋯,k(30)

原始可行性(Primal feasibility):gi(w∗)≤0,i=1,2,⋯,k(31)

对偶可行性(Dual feasibility):α∗≥0,i=1,2,⋯,k(32)

互补松弛其实已经包含了原始可行性与对偶可行性。
当 gi(w∗)<0 ，只有当 α∗=0 ，互补松弛才成立；
当 α∗>0 ，只有当 gi(w∗)=0 ，互补松弛才成立。

我们的求解目标经历了以下转化：

通过几何分析（几何间隔的意义）得到式（15）最初始的目标函数⟹通过几何间隔与函数间隔的关系与一些约束与手段，从式（15）得到常用的且较正规的目标函数式（17），此时它是一个凸函数⟹引入拉格朗日算子将目标函数式（17）变成式（19）的原始问题⟹每个原始问题都有对应的对偶问题，满足KKT条件后对偶问题的解与原始问题的解相等，可通过求解对偶问题式（25）来获得原始问题式（19）的解

经过这一系列转化，结论就是，求解得到对偶问题的解之后，就能得到目标函数的参数 w,b ，获得最后的SVM分类函数。为什么要绕这么一大圈去求解对偶问题？
一是对偶问题往往比原始问题更容易求解，二是对偶问题有一些优良的结构，可以在内积中自然而然地引入核函数，进而推广到非线性分类问题，而且还可以用软间隔分类器来解决非线性问题。

2.1.3、对偶问题的初步求解

接下来讨论如何求解对偶问题。
回到式（25）的对偶问题：

maxα≥0θD(α)=maxα≥0minw,bL(w,b,α)

要求解得到最后的参数，对偶问题的求解方法分成两步。
第一步， minw,bL(w,b,α) 。把 α 当成常数，对 w,b 求 L(w,b,α) 的最小值，然后把用 α 表示的 w,b 代回 L(w,b,α) 中，此时的 L(w,b,α) 成为了参数 α 的函数，实际上是 L(α) ，形式上用 W(α) 表示。
第二步， maxα≥0minw,bL(w,b,α)=maxα≥0W(α) 。对 W(α) 求最大值，此时解出来的 α 是确切的常数，再把这些常数代回第二步中“用 α 表示的 w,b ”中，即可得到最终的参数 w,b 。
本小节只做第一步的处理，第二步的处理将在第三章“SVM的求解”中介绍。

对 w,b 求 L(w,b,α) 的最小值的方式是，分别对 w,b 求偏导，然后让它们的结果为0。
把 L(w,b,α) 的原式（见式（19））稍微展开（ w 被认为是常数 ，所以 wT=w ）：

L(w,b,α)=12∥w∥2−∑i=1mαi[y(i)(wTx(i)+b)−1]=12∥w∥2−∑i=1mαiy(i)wTx(i)+b∑i=1mαiy(i)+∑i=1mαi(33)

对 w 求偏导可以简单得到：

∇wL(w,b,α)=w−∑i=1mαiy(i)x(i)=0⟹w=∑i=1mαiy(i)x(i)(34)

同样，对 b 求偏导可以得到：

∇bL(w,b,α)=∑i=1mαiy(i)=0(35)

这里， x(i) 与 y(i) 是样本点，是已知数，所以我们就有了“用 α 表示的 w与b ”。接下来我们把式（34）与式（35）代回到式（33）中，需要注意的地方是 ∥w∥2=wTw ，其它的正常展开就行，得到：

L(w,b,α)=∑i=1mαi−12∑i,j=1my(i)y(j)αiαj(x(i))Tx(j)=W(α)(36)

再把 (x(i))Tx(j) 用 ⟨x(i),x(j)⟩ 表示，同时把上面与 α 有关的约束条件加上，就到了要求解的对偶问题的第二步：

maxαs.t.W(α)=∑i=1mαi−12∑i,j=1my(i)y(j)αiαj⟨x(i),x(j)⟩αi≥0,i=1,2,⋯,m∑i=1mαiy(i)=0(37)

注意，我们的目标是求得参数 w,b ， w 在式（34）中有描述，当我们把 maxαW(α) 求解出来，得到 αi 配合上样本点，即可计算出 w 的实际值，那么， b 是如何计算的？
这里是 b 的计算方法：

b∗=−maxi:y(i)=−1w∗Tx(i)+mini:y(i)=1w∗Tx(i)2(38)

再一次把图一贴上来：

式（38）中， −maxi:y(i)=−1w∗Tx(i) 表示，过分类为-1的支持向量的超平面的截距，对应图中过圈圈的下面那条虚线的截距； −mini:y(i)=1w∗Tx(i) 表示，过分类为1的支持向量的超平面的截距，对应图中过叉叉的上面那条虚线的截距。
实线即超平面的截距是这两个截距的和的一半。

到这里，我们完成了 minw,bL(w,b,α) 的过程，对偶问题的第一步求解就完成了。要求得截距 b 我们需要知道 w ，而 w 需要用 α 计算得到，所以整个SVM分类器的求解只剩下最后一步了。
对偶问题的第二步 maxα≥0W(α) ，求解 α 的介绍将在第三章中进行（第三章中将要求解的是经过优化的 W(α) ，不是现在这个），因为接下来要介绍两个内容，核函数与软间隔分类器。

2.2、SVM优化一——引入核函数（Kernel）

2.2.1、核函数的作用

核函数的作用：把原坐标系里线性不可分的数据投影到另一个空间，尽量使得数据在新的空间里线性可分。
为了有一个直观感受可以看这个视频：https://www.youtube.com/watch?v=3liCbRZPrZA

低维空间（这里是二维）里有红色与蓝色两种不同的分类点，可以看到在这里它们线性不可分：

图四

用核函数把低维空间里的数据投影到高维空间（这里是三维）中去：


图五

在高维空间中做一个超平面将数据分类：


图六

高维空间中的分类超平面，表现在低维空间中，就是那个发光的圆：


图七

可以看到，即使原空间中的数据线性不可分，也可以获得很好的分类超平面，这就是核函数在SVM中的作用。

2.2.2、核函数本身

将数据映射到高维空间

让我们来看式（37）中可以使用核函数的地方：

W(α)=∑i=1mαi−12∑i,j=1my(i)y(j)αiαj⟨x(i),x(j)⟩

令 x(i)=x ， x(j)=z ，我们可以将尖括号中的内积 ⟨x(i),x(j)⟩ 替换成 ⟨ϕ(x),ϕ(z)⟩ ， ϕ(x) 表示向量之间的映射，一般是从低维到高维：

W(α)=∑i=1mαi−12∑i,j=1my(i)y(j)αiαj⟨ϕ(x),ϕ(z)⟩(39)

给定了一个特征映射 ϕ ，我们将相应的核函数定义为：

K(x,z)=⟨ϕ(x),ϕ(z)⟩=ϕ(x)Tϕ(z)(40)

这是李航老师《统计学习方法》SVM章节中给出的例子，我来简述一下：

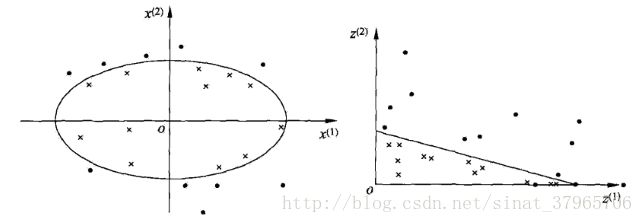
图八
x 是原空间的数据， x=[x(1)x(2)] ；
同时， z=ϕ(x)=[(x(1))2(x(2))2] （这里的 z 指的是 映射后的向量，跟 x(j)=z 的设定—— 原空间中的向量——冲突了，但是因为图上给的是 z ，所以还是这么用了，请读者自行区分一下）。
映射过后，原空间中的点相应地变为新空间中的点，原空间中的椭圆：

w1(x(1))2+w2(x(2))2+b=0(41)

变成了新空间中的直线：

w1z(1))+w2z(2))+b=0(42)

线性不可分问题一般来说不好求解。所以我们将数据映射到高维空间，在高维空间里使用求解线性可分问题的方法，来求解在原空间中线性不可分的问题。
我们看到虽然样本点经过了映射，但是参数 w,b 却没变，因为式（39）与式（40）中的 w,b 本来就是相同的，只是在不同维度中表现出不同的样子而已（在（这里的）高维空间里表现为一条直线，在低维空间里表现为一个椭圆）。
这些跟图四到图七所表达的意思也是很吻合的。

化解计算量问题

将数据映射到高维空间，在高维空间中去寻找线性超平面的这个方式固然好，但是却引来了新的问题。
ϕ(x) 是映射后的数据，一般比原数据更高维，而真正使用的时候，还是在计算它的内积 ϕ(x)Tϕ(z) ，这样的计算代价太高昂了。
核函数的一个巧妙之处在于，可以通过计算低维向量内积的平方，得到高维向量的内积，下面是一个例子。
如果我们有一个核函数如下，并且 x,z 都是 n<