图形变换之旋转变换公式推导
文章目录
- 齐次坐标[^3]
- 二维旋转变换
- 三维旋转变换
- 绕 z 轴旋转
- 绕 x 轴旋转
- 绕 y 轴旋转
- 总结
- 例子
齐次坐标1
齐次坐标表示法就是用 n+1 维向量表示一个 n 维向量。
n 维空间中的点的位置向量用非齐次坐标表示时, ( P 1 , P 2 , … , P n ) (P_1,P_2,…, P_n) (P1,P2,…,Pn) 具有 n 个坐标分量,并且是唯一的。如果用齐次坐标表示时,该向量有 n+1 个坐标分量, ( h P 1 , h P 2 , … , h P n , h ) (hP_1, hP_2,…, hP_n, h) (hP1,hP2,…,hPn,h) 并且是不唯一的。2
通常都使 h=1。如果 h≠0,就可以用除齐次坐标的各分量,这一方法称之为齐次坐标的规范化。经过规范化后的齐次坐标就是唯一的。
h = 0 时,该点表示一无穷远点3。三元组 (0, 0, 0) 不表示任何点。原点表示为 (0, 0, 1)
如二维点 (x,y) 的齐次坐标表示为 ( h x , h y , h ) (h_x,h_y,h) (hx,hy,h) ,则 ( h 1 x , h 1 y , h 1 ) , ( h 2 x , h 2 y , h 2 ) , … , ( h m x , h m y , h m ) (h_1x,h_1y,h_1) , (h_2x,h_2y,h_2) ,…, (h_mx,h_my,h_m) (h1x,h1y,h1),(h2x,h2y,h2),…,(hmx,hmy,hm) 都是表示二维空间中的同一个点三维空间中的坐标点的齐次坐标可表示为 (x,y,1) 。
应用齐次坐标可以有效地用矩阵运算把二维、三维甚至更高维空间中点集从一个坐标系转换到另一个坐标系中。
二维齐次坐标变换矩阵的形式为
T 2 D = [ a d g b e h c f i ] T_{2D} = \begin{bmatrix} a & d & g \\ b & e & h \\ c & f & i \\ \end{bmatrix} T2D=⎣⎡abcdefghi⎦⎤

三维齐次坐标变换矩阵的形式为
T 3 D = [ a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 ] T_{3D} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{bmatrix} T3D=⎣⎢⎢⎡a11a21a31a41a12a22a32a42a13a23a33a43a14a24a34a44⎦⎥⎥⎤

二维旋转变换
下面是一个简单的绕原点旋转变换的图。

本文我们关注的是怎么得到变换之后的坐标,而对于变换后的坐标,很多教材上都只有一个简略的结果,并不会给出详细的推导过程。今天学习旋转变换的时候,对怎么得出变换后的坐标产生了疑惑,花了几分钟才想明白,特此记录一下。

我们不妨设变换前图形上任意一点的坐标为 P ( x , y ) P(x, y) P(x,y),变换后图形上对应点坐标为 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 。
对于旋转变换来说,我们不妨设旋转角度为 θ,即 ∠ P O P ′ = θ \angle POP' = \theta ∠POP′=θ。我们现在就来推导一下 x ′ x' x′ 和 y ′ y' y′ 关于 x, y 的表示法。(应该还有更好的证法)
由旋转的性质易知 O P = O P ′ = x 2 + y 2 = d OP = OP' = \sqrt{x^2 + y^2} = d OP=OP′=x2+y2=d
不妨设 ∠ P O x = α \angle POx = \alpha ∠POx=α,有 s i n α = y d sin\alpha = \dfrac{y}{d} sinα=dy, c o s α = x d cos\alpha = \dfrac{x}{d} cosα=dx。又有下面这两个方程:
s i n ( α + θ ) = y ′ d c o s ( α + θ ) = x ′ d sin(\alpha + \theta) = \dfrac{y'}{d} \newline cos(\alpha + \theta) = \space \space \dfrac{x'}{d} sin(α+θ)=dy′cos(α+θ)= dx′
把这两个方程解出来就可以得到 x’ 和 y’ 的值了(把 sin(a+θ),cos(a+θ) 拆开后,sin a 和 cos a 都已知,把 d 乘过去就行,这里打方程不方便就不敲出具体拆解过程了):
x ′ = x c o s θ − y s i n θ y ′ = x s i n θ + y c o s θ x' = xcos\theta - ysin\theta \newline y' = xsin\theta + ycos\theta \newline x′=xcosθ−ysinθy′=xsinθ+ycosθ
因此有如下推导
P ′ = [ x ′ y ′ 1 ] = [ x c o s θ − y s i n θ x s i n θ + y c o s θ 1 ] = [ x y 1 ] [ c o s θ s i n θ 0 − s i n θ c o s θ 0 0 0 1 ] = P ・ R ( θ ) P' = [x'\space\space y'\space\space 1]=[xcos\theta - ysin\theta \space\space xsin\theta + ycos\theta \space\space 1]=[x\space\space y \space\space 1]\begin{bmatrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}=P・R(\theta) P′=[x′ y′ 1]=[xcosθ−ysinθ xsinθ+ycosθ 1]=[x y 1]⎣⎡cosθ−sinθ0sinθcosθ0001⎦⎤=P・R(θ)4
其坐标变换矩阵 R ( θ ) R(\theta) R(θ) 如下
[ c o s θ s i n θ 0 − s i n θ c o s θ 0 0 0 1 ] \begin{bmatrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} ⎣⎡cosθ−sinθ0sinθcosθ0001⎦⎤
三维旋转变换
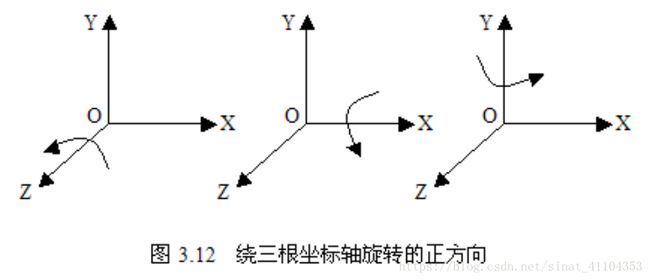
分别绕三根坐标轴旋转的时候,有一个坐标是不变的,然后我们把另外两个当成二维的算就行,我们可以分别得出对应的坐标变换矩阵:
绕 z 轴旋转
[ c o s θ s i n θ 0 0 − s i n θ c o s θ 0 0 0 0 1 0 0 0 0 1 ] \begin{bmatrix} cos\theta & sin\theta & 0 & 0 \\ -sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡cosθ−sinθ00sinθcosθ0000100001⎦⎥⎥⎤
绕 x 轴旋转
[ 1 0 0 0 0 c o s θ s i n θ 0 0 − s i n θ c o s θ 0 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\theta & sin\theta & 0 \\ 0 & -sin\theta & cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡10000cosθ−sinθ00sinθcosθ00001⎦⎥⎥⎤
绕 y 轴旋转
[ c o s θ 0 − s i n θ 0 0 1 0 0 s i n θ 0 c o s θ 0 0 0 0 1 ] \begin{bmatrix} cos\theta & 0 & -sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ sin\theta & 0 & cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡cosθ0sinθ00100−sinθ0cosθ00001⎦⎥⎥⎤
如果说要记得话,一个简单的记法是绕哪个轴旋转哪个轴上就没有 cos sin 之类的。
总结
这个总结可以不看,现在我也看不懂了。
我们不难发现核心部分基本和二维都是差不多的,除了绕 y 轴旋转的那个 sinθ 的正负号反了。那么我们有没有想过为什么就它是反的呢?一个歪理如下:因为核心部分 [ c o s θ s i n θ − s i n θ c o s θ ] \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \\ \end{bmatrix} [cosθ−sinθsinθcosθ]被分开了
- 对于绕 z 轴旋转,观察到 x 一直在减小
- 对于绕 x 轴旋转,观察到 y 一直在减小
- 对于绕 y 轴旋转,观察到 z 一直在减小
而坐标变换矩阵中,谁减小,负号就在谁的 sinθ 那里。
例子
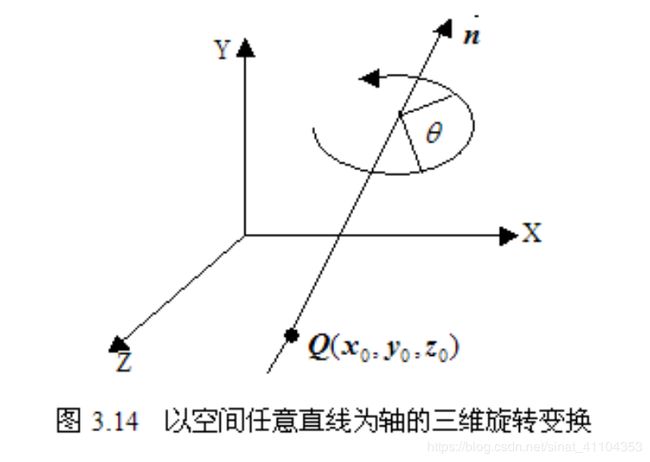
例:设三维空间中有一条任意直线,它由直线上一点 Q 和沿直线方向的单位方向向量 n 确定。Q 点坐标为 ( x 0 , y 0 , z 0 ) (x_0, y_0, z_0) (x0,y0,z0),直线向量 n = [ n 1 , n 2 , n 3 ] [n_1, n_2, n_3] [n1,n2,n3] ,|n| = n 1 2 + n 2 2 + n 3 2 \sqrt{{n_1}^2+{n_2}^2+{n_3}^2} n12+n22+n32 = 1。求绕这条直线旋转 θ \theta θ 角的旋转变换矩阵
- 实现该变换可以先做平移变换,使旋转轴成为通过坐标原点的一条直线,然后做绕通过坐标原点的旋转轴旋转 θ \theta θ 角的旋转变换,最后再做平移变换,即开始所作平移变换的逆变换,使旋转轴平移回到原来的位置。
- 过坐标原点的任意直线为旋转轴的旋转变换可分为五步实现:
- 做绕 X 轴旋转 α \alpha α 角的变换,使旋转轴落在 Y=0 上。
- 做绕 Y 轴旋转 β \beta β 角的变换,使旋转轴与 Z 轴重合。
- 做绕 Z 轴旋转 θ \theta θ 角的旋转变换。
- 做第 2 步的逆变换,即做绕 Y 轴 - α \alpha α 旋转变换。
- 做第 1 步的逆变换,即做绕 X 轴 - β \beta β 旋转变换。
我们不妨假设由向量 ON 表示直线向量 n = [ n 1 , n 2 , n 3 ] [n_1, n_2, n_3] [n1,n2,n3],其中 O 为原点,N 坐标为 ( n 1 , n 2 , n 3 ) (n_1, n_2, n_3) (n1,n2,n3)。对题中直线平移到原点后,绕题中的直线旋转就相当于绕 ON 旋转。
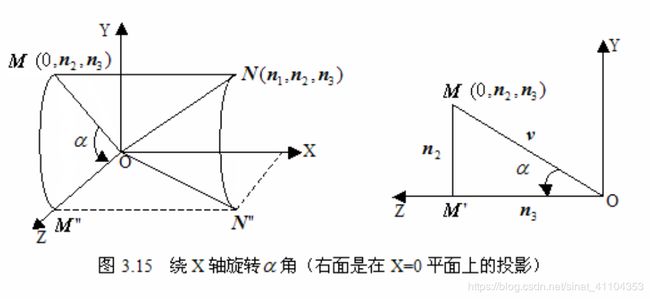
我们要确定的值是 α \alpha α 和 β \beta β 这两个角,首先我们来看 α \alpha α
α \alpha α 是绕 X 轴旋转的变换的角,使平面 OMN 落在 Y=0 上成为 O M ′ ′ N ′ ′ OM''N'' OM′′N′′
s i n α = M ′ M O M = n 2 v sin\alpha = \dfrac{M'M}{OM} = \dfrac{n_2}{v} sinα=OMM′M=vn2
c o s α = M ′ O O M = n 3 v cos\alpha = \dfrac{M'O}{OM} = \dfrac{n_3}{v} cosα=OMM′O=vn3
其中 O M = v = n 2 2 + n 3 2 OM = v = \sqrt{{n_2}^2+{n_3}^2} OM=v=n22+n32,M’ 为 M 到 OZ 的垂足。
由于是绕 X 轴旋转,故其旋转矩阵为
R x ( α ) = [ 1 0 0 0 0 c o s α s i n α 0 0 − s i n α c o s α 0 0 0 0 1 ] = [ 1 0 0 0 0 n 3 v n 2 v 0 0 − n 2 v n 3 v 0 0 0 0 1 ] R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\alpha& sin\alpha& 0 \\ 0 & -sin\alpha& cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \dfrac{n_3}{v} & \dfrac{n_2}{v} & 0 \\ 0 & -\dfrac{n_2}{v} & \dfrac{n_3}{v} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rx(α)=⎣⎢⎢⎡10000cosα−sinα00sinαcosα00001⎦⎥⎥⎤=⎣⎢⎢⎢⎢⎡10000vn3−vn200vn2vn300001⎦⎥⎥⎥⎥⎤
N ′ = [ n 1 , n 2 , n 3 , 1 ] R x ( α ) = [ n 1 , 0 , v , 1 ] N' = [n_1, n_2, n_3, 1] R_x(\alpha) = [n_1, 0, v, 1] N′=[n1,n2,n3,1]Rx(α)=[n1,0,v,1]
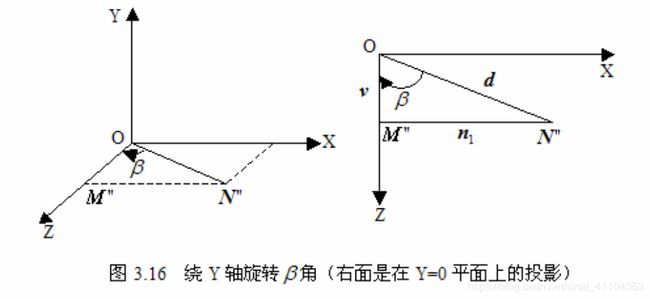
然后我们再来看 β \beta β, β \beta β 是在第一步的基础上绕 Y 轴旋转 O N ′ ′ ON'' ON′′ 使得 O N ′ ′ ON'' ON′′ 落在 Z 轴上
由第一步我们已经知道 M ′ ′ N ′ ′ = M N = n 1 M''N'' = MN = n_1 M′′N′′=MN=n1, d = O N ′ ′ = O N = n 1 2 + n 2 2 + n 3 2 = 1 d = ON'' = ON = \sqrt{{n_1}^2+{n_2}^2+{n_3}^2} = 1 d=ON′′=ON=n12+n22+n32=1,所以有
s i n β = − M ′ ′ N ′ ′ O N ′ ′ = − n 1 d = − n 1 sin\beta= -\dfrac{M''N''}{ON''} = -\dfrac{n_1}{d}=-n_1 sinβ=−ON′′M′′N′′=−dn1=−n15
c o s β = M ′ ′ O O N ′ ′ = d 2 − n 1 2 d = d 2 − n 1 2 = n 2 2 + n 3 2 = v cos\beta= \dfrac{M''O}{ON''} = \dfrac{\sqrt{d^2-{n_1}^2}}{d}=\sqrt{d^2-{n_1}^2}=\sqrt{n_2^2+n_3^2}=v cosβ=ON′′M′′O=dd2−n12=d2−n12=n22+n32=v
由于 β \beta β 是绕 Y 轴旋转,故其旋转矩阵为
R y ( β ) = [ c o s β 0 − s i n β 0 0 1 0 0 s i n β 0 c o s β 0 0 0 0 1 ] = [ v 0 n 1 0 0 1 0 0 − n 1 0 v 0 0 0 0 1 ] R_y(\beta) = \begin{bmatrix} cos\beta & 0 & -sin\beta& 0 \\ 0 & 1 & 0 & 0 \\ sin\beta& 0 & cos\beta& 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} v & 0 & n_1 & 0 \\ 0 & 1 & 0 & 0 \\ -n_1 & 0 & v & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Ry(β)=⎣⎢⎢⎡cosβ0sinβ00100−sinβ0cosβ00001⎦⎥⎥⎤=⎣⎢⎢⎡v0−n100100n10v00001⎦⎥⎥⎤
N ′ ′ = [ n 1 , 0 , v , 1 ] R y ( β ) = [ 0 , 0 , 1 , 1 ] N'' = [n_1, 0, v, 1]R_y(\beta)=[0,0,1,1] N′′=[n1,0,v,1]Ry(β)=[0,0,1,1]
R z ( θ ) = [ c o s θ s i n θ 0 0 − s i n θ c o s θ 0 0 0 0 1 0 0 0 0 1 ] R_z(\theta)=\begin{bmatrix} cos\theta & sin\theta & 0 & 0 \\ -sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rz(θ)=⎣⎢⎢⎡cosθ−sinθ00sinθcosθ0000100001⎦⎥⎥⎤
回到 5 个步骤
- 做绕 X 轴旋转 α \alpha α 角的变换,使旋转轴落在 Y=0 上。
- 做绕 Y 轴旋转 β \beta β 角的变换,使旋转轴与 Z 轴重合。
- 做绕 Z 轴旋转 θ \theta θ 角的旋转变换。
- 做第 2 步的逆变换,即做绕 Y 轴 - α \alpha α 旋转变换。
- 做第 1 步的逆变换,即做绕 X 轴 - β \beta β 旋转变换。
五个步骤用旋转矩阵表示出来如下:
R ( θ ) = R x ( α ) ・ R y ( β ) ・ R z ( θ ) ・ R y ( − β ) ・ R x ( − α ) = R(\theta)=R_x(\alpha)・R_y(\beta)・R_z(\theta)・R_y(-\beta) ・R_x(-\alpha) = R(θ)=Rx(α)・Ry(β)・Rz(θ)・Ry(−β)・Rx(−α)=
[ 1 0 0 0 0 n 3 v n 2 v 0 0 − n 2 v n 3 v 0 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \dfrac{n_3}{v} & \dfrac{n_2}{v} & 0 \\ 0 & -\dfrac{n_2}{v} & \dfrac{n_3}{v} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎢⎢⎡10000vn3−vn200vn2vn300001⎦⎥⎥⎥⎥⎤ ・ [ v 0 n 1 0 0 1 0 0 − n 1 0 v 0 0 0 0 1 ] \begin{bmatrix} v & 0 & n_1 & 0 \\ 0 & 1 & 0 & 0 \\ -n_1 & 0 & v & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡v0−n100100n10v00001⎦⎥⎥⎤ ・ [ c o s θ s i n θ 0 0 − s i n θ c o s θ 0 0 0 0 1 0 0 0 0 1 ] \begin{bmatrix} cos\theta & sin\theta & 0 & 0 \\ -sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡cosθ−sinθ00sinθcosθ0000100001⎦⎥⎥⎤ ・ [ v 0 − n 1 0 0 1 0 0 n 1 0 v 0 0 0 0 1 ] \begin{bmatrix} v & 0 & -n_1 & 0 \\ 0 & 1 & 0 & 0 \\ n_1 & 0 & v & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡v0n100100−n10v00001⎦⎥⎥⎤ ・ [ 1 0 0 0 0 n 3 v − n 2 v 0 0 n 2 v n 3 v 0 0 0 0 1 ] = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \dfrac{n_3}{v} & -\dfrac{n_2}{v} & 0 \\ 0 & \dfrac{n_2}{v} & \dfrac{n_3}{v} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}= ⎣⎢⎢⎢⎢⎡10000vn3vn200−vn2vn300001⎦⎥⎥⎥⎥⎤=
[ n 1 2 + ( 1 − n 1 2 ) c o s θ n 1 n 2 ( 1 − c o s θ ) + n 3 s i n θ n 1 n 3 ( 1 − c o s θ ) − n 2 s i n θ 0 n 1 n 2 ( 1 − c o s θ ) − n 3 s i n θ n 2 2 + ( 1 − n 2 2 ) c o s θ n 2 n 3 ( 1 − c o s θ ) + n 1 s i n θ 0 n 1 n 3 ( 1 − c o s θ ) + n 2 s i n θ n 2 n 3 ( 1 − c o s θ ) − n 1 s i n θ n 3 2 + ( 1 − n 3 2 ) c o s θ 0 0 0 0 1 ] \begin{bmatrix} n_1^2+(1-n_1^2)cos\theta & n_1n_2(1-cos\theta)+n_3sin\theta & n_1n_3(1-cos\theta)-n_2sin\theta & 0 \\ n_1n_2(1-cos\theta)-n_3sin\theta & n_2^2+(1-n_2^2)cos\theta & n_2n_3(1-cos\theta)+n_1sin\theta & 0 \\ n_1n_3(1-cos\theta)+n_2sin\theta & n_2n_3(1-cos\theta)-n_1sin\theta & n_3^2+(1-n_3^2)cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡n12+(1−n12)cosθn1n2(1−cosθ)−n3sinθn1n3(1−cosθ)+n2sinθ0n1n2(1−cosθ)+n3sinθn22+(1−n22)cosθn2n3(1−cosθ)−n1sinθ0n1n3(1−cosθ)−n2sinθn2n3(1−cosθ)+n1sinθn32+(1−n32)cosθ00001⎦⎥⎥⎤
齐次坐标可让包括无穷远点的点坐标以有限坐标表示 ↩︎
[计算机图形学 第四版]: 齐次坐标(homogeneous coordinate)这一术语在数学中用来指出笛卡尔方程的表达效果。当笛卡尔点 (x, y) 转换成齐次坐标 ( x h , y h , h ) (x_h, y_h, h) (xh,yh,h) 时,包含 x 和 y 的方程 f(x, y) = 0 变成了三个参数 x h , y h 和 h x_h, y_h 和 h xh,yh和h 的齐次方程。这恰好说明,假如三个参数均被各自乘上值 v 后的值替换,那么 v 可以从方程中作为因子提取出来。 ↩︎
[维基百科,齐次坐标]: 一条通过原点 (0, 0) 的线之方程可写作 nx+my = 0,其中 n 及 m 不能同时为 0。以参数表示,则能写成 x=mt, y=-nt。令 Z=1/t,则线上的点之笛卡尔坐标可写作 (m/Z, -n/Z)。在齐次坐标下,则写成 (m, -n, Z)。当 t 趋向无限大,亦即点远离原点时,Z 会趋近于 0,而该点的齐次坐标则会变成 (m, -n, 0)。因此,可定义 (m, -n, 0) 为对应 nx+my=0 这条线之方向的无穷远点之齐次坐标。因为欧式平面上的每条线都会与透过原点的某一条线平行,且因为平行线会有相同的无穷远点,欧式平面每条线上的无穷远点都有其齐次坐标。 ↩︎
[维基百科,齐次坐标]: 有些作者会使用不同的符号表示齐次坐标,以与笛卡尔坐标相区别,如以冒号代替逗号,如以 (x:y:z) 代替 (x, y, z),以强调该坐标有着比例的性质。亦有以方括号代替括弧,如以 [x, y, z] 来强调有多个坐标表示同一个点。有些作者则会同时使用冒号与方括号,如 [x:y:z]。 ↩︎
这里 s i n β sin\beta sinβ 是负的是因为 β \beta β 是顺时针旋转,我们默认逆时针方向为正方向。 ↩︎