【数学建模】数据处理问题

一、插值与拟合

常用于数据的补全以及趋势分析

1、插值

总的思想，就是利用函数f (x)若干已知点的函数值，求出适当的特定函数g(x)。这样f(x)其他未知点上的值，就可以用g(x)在这一点的值来近似。这种通过已知求未知的方法称为-----插值。

插值方法有很多，个人感觉样条插值spline最常用吧。。。其他感觉要么复杂要么不靠谱。

对了，二维散乱插值有个方法叫v4，效果不错，拿来用就是了。。。

基本内容：

• 一维插值
• 二维有序插值
• 二维散乱插值

基本语法：

y = interp1（x0,y0,x,'spline'）;		%一维插值
%x0必须单调；x要落在x0区间范围内；x指的是待求的值

%示例
hours=1:12;
temps=[5 8 9 15 25 29 31 30 22 25 27 24];
h=1:0.1:12;
t=interp1(hours,temps,h,'spline'); 

y = interp2（x0,y0,z0,x,y,'spline'）;		%二维插值--规则点
%x0,y0必须单调；x,y是一个是行向量一个是列向量;x,y要落在x0,y0区间范围内；(x,y)指的是待求的坐标

%示例
x=1:5;
y=1:3;
temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
xi=1:0.2:5;
yi=1:0.2:3;
zi=interp2(x,y,temps,xi',yi,'spline');

y = interp2（x0,y0,z0,x,y,'v4'）;		%二维插值--散乱点

%示例
x=[129.0  140.0  103.5  88.0  185.5  195.0  105.5 157.5  107.5  77.0  81.0  162.0  162.0  117.5 ];
y=[ 7.5  141.5  23.0  147.0  22.5  137.5  85.5      -6.5  -81  3.0  56.5  -66.5  84.0  -33.5 ];
z=[ 4  8  6  8  6  8  8  9  9  8  8  9  4  9 ];
x1=75:1:200;
y1=-50:1:150;
[x1,y1]=meshgrid(x1,y1);
z1=griddata(x,y,z,x1,y1,'v4');

2、拟合：

总的的说，已知一组已知数据，寻求一个函数y = f (x)，使 f (x)在某种准则下与所有数据点最为接近，即曲线拟合得最好。
按照函数的不同，可以将拟合问题进行分类。
感觉多项式拟合比线性最小二乘法实用多了，就合并了吧23333

基本内容：

• 多项式拟合（合并线性最小二乘法）
• 指定函数拟合

基本语法：

a=polyfit(x0,y0,m)		%多项式拟合，线性最小二乘法就是使m=1
%m是最高次项系数，a返回m+1维向量（还有一个常数项系数）

%示例：
x=[1 2 3 4 5 6 7 8 9];
y=[9 7 6 3 -1 2 5 7 20];
P=polyfit(x,y,3)

%指定函数拟合---看着头晕，贴一段代码要用直接调参就行
syms t;
x=[0 0.4 1.2 2 2.8 3.6 4.4 5.2 6 7.2 8 9.2 10.4 11.6 12.4 13.6 14.4 15];
y=[1 0.85 0.29 -0.27 -0.53 -0.4 -0.12 0.17 0.28 0.15 -0.03 -0.15 -0.071 0.059 0.08 0.032 -0.015 -0.02];
f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});	%输入要拟合的函数，以及参数，自变量等，自定义拟合函数
cfun=fit(x',y',f)  %显示拟合后的结果
xi=0:.1:20;
yi=cfun(xi);
plot(x',y','r*',xi,yi,'b--')；

区别：
插值一般经过所有数据点，拟合不一定经过所有数据点
插值不一定得到近似函数的表达形式，仅找到未知点对应值。拟合要求得到一个具体的近似函数表达式。
通常建议：数据比较准确，用插值；数据误差较大，用拟合

参考资料：

数学建模之拟合插值方法
数学建模-插值与拟合模型
数学建模常规算法：插值和拟合

二、K-means聚类与高斯混合聚类

常用于数据异常值诊断与剔除。
通过聚类检测离群点，进而进行删除

1、 K-means聚类

2、高斯混合聚类

涉及到聚类的知识，怪复杂的，等学到聚类再写吧。。。

三、主成分分析

常用于多维数据的降维，减少数据的冗余

​主成分分析（PCA）， 用于将多个变量通过线性变换以选出较少个数重要变量。

主成分与原始变量之间的关系：

​ （1）主成分保留了原始变量绝大多数信息。

​ （2）主成分的个数大大少于原始变量的数目。

​ （3）每个主成分都是原始变量的线性组合。

​ （4）每个主成分的贡献率不同。

​ （5）各个主成分之间互不相关。

处理步骤：

1. 数据标准化
2. 计算相关系数矩阵
3. 计算特征值与特征向量
4. 求出贡献率与累计贡献率（一般累计贡献率达到85%即可）
5. 计算主成分载荷（即线性系数）与主成分得分

代码：

%示例：
da=xlsread('data.xlsx');
%%标准化矩阵 
da=zscore(da);
fprintf('相关系数矩阵：\n') 
std=corrcoef(da)     	 %计算相关系数矩阵 
[vec,val]=eig(std);  	 %求特征值(val)及特征向量(vec) 
newval=diag(val) ;    
[y,i]=sort(newval) ;   	%对特征根进行排序，y 为排序结果，i 为索引 
fprintf('特征根排序：\n')
for   z=1:length(y)     
    newy(z)=y(length(y)+1-z); 
end
fprintf('%g\n',newy)  	%%显示特征根
rate=y/sum(y); 
fprintf('贡献率：\n') 
newrate=newy/sum(newy) 
sumrate=0; 
newi=[]; 
for k=length(y):-1:1     
    sumrate=sumrate+rate(k);     
    newi(length(y)+1-k)=i(k);     
    if sumrate>0.85 		%记下累积贡献率大于85%的特征值的序号放入 newi 中 
        break;     
    end
end       
fprintf('主成分数：%g\n\n',length(newi)); 
for p=1:length(newi)     
    for q=1:length(y)      
        vector2(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));%%%主成分载荷     
    end
end
fprintf('显示载荷:\n'); 
disp(vector2); %显示载荷 %%%求各主成分得分 
sco=da*vector2; 
csum=sum(sco,2); 
[newcsum,i]=sort(-1*csum); 
[newi,j]=sort(i); 
fprintf('计算得分：\n') %得分矩阵：sco 为各主成分得分；csum 为综合得分；j 为排序结果 
score=[sco,csum,j]

参考资料：
关于主成分分析matlab代码实现的总结
数学建模算法笔记（2）——主成分分析
数学建模之主成分分析matlab
数学建模之主成分分析法

四、方差分析与协方差分析

常用于数据截取与特征选择。通俗的来说，就是判断某个特征对结果对影响是否显著。

1、方差分析

（1）单因素方差分析

维持其他因素保持不变，仅仅对一个因素进行考虑并计算方差，这称为单因素方差分析。

数据集分为均衡数据（各组数据个数相等）与非均衡数据（各组数据个数不等）。

%均衡数据
p=anova1(x)		%p是一个概率;x每一行代表不同样本，每一列代表特征中的不同序号

%示例
x=[162 158 146 150
167 160 154 155
170 164 162 161
175 172 168 180];

p=anova1(x)

求得 p=0.1109>0.05，所以几种工艺制成的灯泡寿命没有显著差异

%非均衡数据
p=anova1(x,group)	%x为向量，从第1组到第r组数据依次排列;roup为与x同长度的向量，标志x中数据的组别（在于x第i组数据相对应的位置出输入整数i)

%示例
x=[1620 1580 1460 1500
1670 1600 1540 1550
1700 1640 1620 1610
1750 1720 1680 1800];
x=[x(1:4),x(16),x(5:8),x(9:11),x(12:15)];
g=[ones(1,5),2*ones(1,4),3*ones(1,3),4*ones(1,4)];
p=anova1(x,g)

求得 0.01

单因素方差分析结果对应一般如下（单因素显著性水平取0.05）：

p值	结果
p<0.01	非常显著
0.01	显著
p>0.05	不显著

（2）双因素方差分析

与单因素方差分析类似，这次我们探究两个因素。对两个因素的实验可能进行一次，或者很多次。

单一观测值：

p=anova2(x)		%x不同列的数据表示单一因素的变化情况，不同行中的数据表示另一因素的变化情况

%示例
x=[58.2 56.2 65.3
49.1 54.1 51.6
60.1 70.9 39.2
75.8 58.2 48.7];
[p,t,st]=anova2(x)

求得p=0.4491 0.7387，均>0.10，表明两个特征不同数据之间的差异对于结果无显著影响。

多观测值：

p=anova2(x,reps)	%如果每一“单元”有不止一个观测值，则用参数reps来表明每个“单元”多个观测值的不同标号，即reps给出重复试验的次数t

%示例
x0=[58.2 52.6 56.2 41.2 65.3 60.8
49.1 42.8 54.1 50.5 51.6 48.4
60.1 58.3 70.9 73.2 39.2 40.7
75.8 71.5 58.2 51.0 48.7 41.4];
x=x0';
[p,t,st]=anova2(x,2)

求得p = 0.0035 0.0260 0.0001，其中第三个参数表明两个特征联合作用下对结果的影响。结果表明，这两个特征的影响均是显著的。

值得注意的是，上式使用转置，保证x的形式如下图所示（需要注意行列分别代表的含义）：

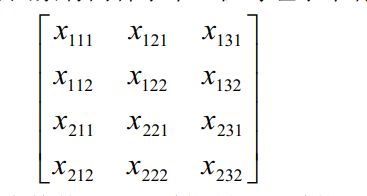
其中，一二维代表特征维，第三维代表样本维。

（3）多因素方差分析

这里用到了正交表的处理方法，我们直接使用anovan函数：

其中，特征样本不同的取值用特征水平1，2，3…来替代。

最后，双因素与多因素方差分析结果对应一般如下（双因素与多因素显著性水平取0.10）：

p值	结果
p<0.01	非常显著
0.01	显著
p>0.10	不显著

2、协方差分析

对于特定的特征，为了寻找那些样本之间差异较大，运用协方差分析。

在进行完方差分析的基础上，进行协方差分析。

%分析列
COMPARISON = multcompare(st,'alpha',0.05, 'estimate','column')
%分析行
COMPARISON = multcompare(st,'alpha',0.05, 'estimate','row')

之后，便可得到答案。

参考资料：
数学建模常用模型19 ：方差分析
数学建模之方差分析