SMO算法实现

数据集以及画图部分代码使用的 https://zhiyuanliplus.github.io/SVM-SMO

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# -- coding: utf-8 --


# 没有使用核函数
def kij(data_x):
    return np.dot(data_x, data_x.T)


def gxi(index, alpha_, y, kij_, b):
    return np.sum(alpha_ * y * (kij_[:, index].reshape(y.shape[0], 1))) + b


def gx(length, alpha_, y, kij_, b):
    g = []
    for i in range(length):
        g.append(gxi(i, alpha_, y, kij_, b))
    return g


def e(g_, y):
    return g_ - y


# 判断是否满足Kkt条件，不满足的话，求出违反的绝对误差
def satisfy_kkt(index, alpha_, eps_, g_, y_, C_, variable_absolute_error):
    val = y_[index] * g_[index]
    if alpha_[index] == 0:
        if val >= 1 - eps_:
            return True
        else:
            variable_absolute_error[index] = abs(1 - eps_ - val)
            return False

    if 0 < alpha_[index] < C_:
        if 1 - eps_ <= val <= 1 + eps_:
            return True
        else:
            variable_absolute_error[index] = max(abs(1 - eps_ - val), abs(val - 1 - eps_))
            return False

    if alpha_[index] == C_:
        if val <= 1 + eps_:
            return True
        else:
            variable_absolute_error[index] = abs(val - 1 - eps)
            return False


def draw(alpha, bet, data, label):
    plt.xlabel(u"x1")
    plt.xlim(0, 100)
    plt.ylabel(u"x2")
    for i in range(len(label)):
        if label[i] > 0:
            plt.plot(data[i][0], data[i][1], 'or')
        else:
            plt.plot(data[i][0], data[i][1], 'og')
    w1 = 0.0
    w2 = 0.0
    for i in range(len(label)):
        w1 += alpha[i] * label[i] * data[i][0]
        w2 += alpha[i] * label[i] * data[i][1]
    w = float(- w1 / w2)

    b = float(- bet / w2)
    r = float(1 / w2)
    lp_x1 = list([10, 90])
    lp_x2 = []
    lp_x2up = []
    lp_x2down = []
    for x1 in lp_x1:
        lp_x2.append(w * x1 + b)
        lp_x2up.append(w * x1 + b + r)
        lp_x2down.append(w * x1 + b - r)
    lp_x2 = list(lp_x2)
    lp_x2up = list(lp_x2up)
    lp_x2down = list(lp_x2down)
    plt.plot(lp_x1, lp_x2, 'b')
    plt.plot(lp_x1, lp_x2up, 'b--')
    plt.plot(lp_x1, lp_x2down, 'b--')
    plt.show()


def smo(X, Y, C, eps, max_iter):
    Kij = kij(X)
    N = X.shape[0]  # 有多少个样本
    
    # 初始值
    alpha = np.zeros(len(X)).reshape(X.shape[0], 1)  # 每个alpha
    b = 0.0
    G = np.array(gx(N, alpha_=alpha, y=Y, kij_=Kij, b=b)).reshape(N, 1)
    G.reshape(N, 1)
    E = e(G, Y)

    visit_j = {}
    visit_i = {}
    loop = 0
    while loop < max_iter:
        # 选择第一个变量
        # 先找到所有违反KKT条件的样本点
        viable_indexes = []  # 所有可选择的样本
        viable_indexes_alpha_less_c = []  # 所有可选择样本中alpha > 0 且 < C的
        viable_indexes_and_absolute_error = {}  # 违反KKT的数量以及违反的严重程度，用绝对值表示
        for i in range(N):
            if not satisfy_kkt(i, alpha, eps, G, Y, C, viable_indexes_and_absolute_error) and i not in visit_i:
                viable_indexes.append(i)
                if 0 < alpha[i] < C:
                    viable_indexes_alpha_less_c.append(i)
        if len(viable_indexes) == 0:  # 找到最优解了，退出
            break
        # 所有可选择样本中 alpha= 0 或 alpha = C的
        viable_indexes_extra = [index for index in viable_indexes if index not in viable_indexes_alpha_less_c]
        i = -1

        # 先选择间隔边界上的支持向量点
        if len(viable_indexes_alpha_less_c) > 0:
            most_obey = -1
            for index in viable_indexes_alpha_less_c:
                if most_obey < viable_indexes_and_absolute_error[index] and index not in visit_i:
                    most_obey = viable_indexes_and_absolute_error[index]
                    i = index
        else:
            most_obey = -1
            for index in viable_indexes_extra:
                if most_obey < viable_indexes_and_absolute_error[index] and index not in visit_i:
                    most_obey = viable_indexes_and_absolute_error[index]
                    i = index
        # 到这里以后，i肯定不为-1
        j = -1

        # 选择|E1 - Ej|最大的那个j
        max_absolute_error = -1
        for index in viable_indexes:
            if i == index:
                continue
            if max_absolute_error < abs(E[i] - E[index]) and index not in visit_j:
                max_absolute_error = abs(E[i] - E[index])
                j = index

        # 找不到j，重新选择i
        if j == -1:
            visit_j.clear()
            visit_i[i] = 1
            continue

        # 假设已经选择到了j
        alpha1_old = alpha[i].copy()  # 这里一定要用copy..因为后面alpha[i]的值会改变，它变了，alpha1_old也随之会变,找了好多原因
        alpha2_old = alpha[j].copy()
        alpha2_new_uncut = alpha2_old + Y[j] * (E[i] - E[j]) / (Kij[i][i] + Kij[j][j] - 2 * Kij[i][j])

        if Y[i] != Y[j]:
            L = max(0, alpha2_old - alpha1_old)
            H = min(C, C + alpha2_old - alpha1_old)
        else:
            L = max(0, alpha2_old + alpha1_old - C)
            H = min(C, alpha2_old + alpha1_old)

        # 剪辑切割
        if alpha2_new_uncut > H:
            alpha2_new = H
        elif L <= alpha2_new_uncut <= H:
            alpha2_new = alpha2_new_uncut
        else:
            alpha2_new = L

        # 变化不大，重新选择j
        if abs(alpha2_new - alpha2_old) < 0.0001:
            visit_j[j] = 1
            continue

        alpha1_new = alpha1_old + Y[i] * Y[j] * (alpha2_old - alpha2_new)

        if alpha1_new < 0:
            visit_j[j] = 1
            continue

        # 更新值
        alpha[i] = alpha1_new
        alpha[j] = alpha2_new

        b1_new = -E[i] - Y[i] * Kij[i][i] * (alpha1_new - alpha1_old) - Y[j] * Kij[i][j] * (alpha2_new - alpha2_old) + b
        b2_new = -E[j] - Y[i] * Kij[i][j] * (alpha1_new - alpha1_old) - Y[j] * Kij[j][j] * (alpha2_new - alpha2_old) + b

        if 0 < alpha1_new < C:
            b = b1_new
        elif 0 < alpha2_new < C:
            b = b2_new
        else:
            b = (b1_new + b2_new) / 2
        # 更新值
        G = np.array(gx(N, alpha_=alpha, y=Y, kij_=Kij, b=b)).reshape(N, 1)
        Y = Y.reshape(N, 1)
        E = e(G, Y)
        print("iter  ", loop)
        print("i:%d from %f to %f" % (i, float(alpha1_old), alpha1_new))
        print("j:%d from %f to %f" % (j, float(alpha2_old), alpha2_new))
        visit_j.clear()
        visit_i.clear()
        loop = loop + 1
        # print(alpha, b)

    return alpha, b


if __name__ == '__main__':
    data = pd.read_csv("data.csv", header=None)
    X = np.array(data.values[:, : -1])
    Y = np.array(data.values[:, -1])
    Y = Y.reshape(X.shape[0], 1)
    C = 1
    eps = 1e-3  # 误差值
    max_iter = 10000  # 最大迭代次数
    alpha, bb = smo(X, Y, C, eps, max_iter)
    print(alpha)
    print(bb)
    draw(alpha, bb, X, Y)
# 注意np.array (n,) 和 (n ,1)是不一样的，（n , 1) - (n, ） = (n, n) 一定要把(n, )转化reshape为(n, 1)

输出结果表明：当迭代到6587次时，所有变量的解都满足KKT条件。

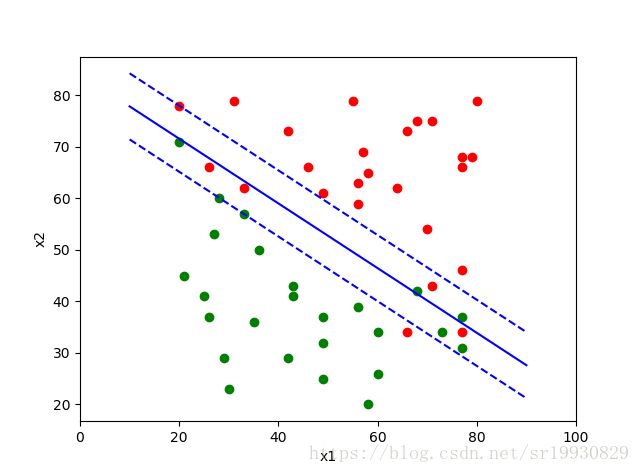
效果图如下：