cs231n作业1--SVM
SVM算法:
1、算法思想:寻找一个超平面来划分不同类别的数据。http://www.cnblogs.com/end/p/3848740.html用图表很好的解释了什么是SVM
2、损失函数公式:
![]() 表示每个样本分类的损失值
表示每个样本分类的损失值
![]() 对所有测试样本的平均损失值
对所有测试样本的平均损失值
3、求导(梯度公式) :
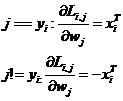
在代码理解过程中遇到了一些问题,为什么一个样本对每个分类都要重复计算一遍第二个公式,这是因为在每一个样本进行损失值计算时,对其他所有非真实类都进行了损失值计算。比如有10个类,就需要计算9次损失函数公式中的第一个公式,相应的在计算梯度过程中就需要叠加计算9次梯度公式中的第一个公式。
4、代码实现:
linear_svm.py:
import numpy as np
from random import shuffle
from past.builtins import xrange
def svm_loss_naive(W, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in xrange(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in xrange(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0:
loss += margin
dW[:,y[i]] += -X[i,:]
dW[:,j] += X[i,:]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /=num_train #
# Add regularization to the loss.
loss += 0.5 * reg * np.sum(W * W)
dW += reg * W
#############################################################################
# TODO: #
# Compute the gradient of the loss function and store it dW. #
# Rather that first computing the loss and then computing the derivative, #
# it may be simpler to compute the derivative at the same time that the #
# loss is being computed. As a result you may need to modify some of the #
# code above to compute the gradient. #
#############################################################################
return loss, dW
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.
Inputs and outputs are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
#############################################################################
# TODO: #
# Implement a vectorized version of the structured SVM loss, storing the #
# result in loss. #
#############################################################################
scores = X.dot(W)
num_train = X.shape[0]
num_classes = W.shape[1]
scores_correct = scores[np.arange(num_train), y]
scores_correct = np.reshape(scores_correct, (num_train, 1))
margins = scores - scores_correct + 1.0
margins[np.arange(num_train), y] = 0.0
margins[margins <= 0] = 0.0
loss += np.sum(margins) / num_train
loss += 0.5 * reg * np.sum(W * W)
#############################################################################
# END OF YOUR CODE #
#############################################################################
#############################################################################
# TODO: #
# Implement a vectorized version of the gradient for the structured SVM #
# loss, storing the result in dW. #
# #
# Hint: Instead of computing the gradient from scratch, it may be easier #
# to reuse some of the intermediate values that you used to compute the #
# loss. #
#############################################################################
# compute the gradient
margins[margins > 0] = 1.0
row_sum = np.sum(margins, axis=1)
margins[np.arange(num_train), y] = -row_sum
dW += np.dot(X.T, margins)/num_train + reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dWsvm.ipynb
# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of about 0.4 on the validation set.
learning_rates = [1e-7, 5e-5]
regularization_strengths = [2.5e4, 5e4]
# results is dictionary mapping tuples of the form
# (learning_rate, regularization_strength) to tuples of the form
# (training_accuracy, validation_accuracy). The accuracy is simply the fraction
# of data points that are correctly classified.
results = {}
best_val = -1 # The highest validation accuracy that we have seen so far.
best_svm = None # The LinearSVM object that achieved the highest validation rate.
################################################################################
# TODO: #
# Write code that chooses the best hyperparameters by tuning on the validation #
# set. For each combination of hyperparameters, train a linear SVM on the #
# training set, compute its accuracy on the training and validation sets, and #
# store these numbers in the results dictionary. In addition, store the best #
# validation accuracy in best_val and the LinearSVM object that achieves this #
# accuracy in best_svm. #
# #
# Hint: You should use a small value for num_iters as you develop your #
# validation code so that the SVMs don't take much time to train; once you are #
# confident that your validation code works, you should rerun the validation #
# code with a larger value for num_iters. #
################################################################################
iters = 2000 #100
for lr in learning_rates:
for rs in regularization_strengths:
svm = LinearSVM()
svm.train(X_train, y_train, learning_rate=lr, reg=rs, num_iters=iters)
y_train_pred = svm.predict(X_train)
acc_train = np.mean(y_train == y_train_pred)
y_val_pred = svm.predict(X_val)
acc_val = np.mean(y_val == y_val_pred)
results[(lr, rs)] = (acc_train, acc_val)
if best_val < acc_val:
best_val = acc_val
best_svm = svm
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)