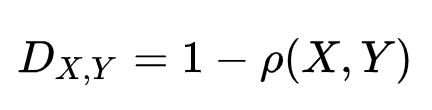支持向量机SVM、高斯核函数_核函数填坑(笔记02）
引入：
输入相同的数据，不同的分类器处理方式不一样，结果也不一样。今天重新填坑核函数，顺便学习一下SVM。
支持向量机，高斯核函数
- 支持向量机的背景介绍
- 核心思想
- 公式和SVM分类
- 公式
- 超平面公式
- 公式推导
- 归一化后的超平面公式
- SVM分类
- 核函数（kernel trick）
- 核心思想
- 为什么要把核函数和SVM结合起来？
- kernel支持向量机的简单流程
- 常见的核函数及其应用
- 名词介绍
- 希尔伯特空间（Hilbert space）
- 内积（inner product）
- 归一化和标准化（normalization vs standardization）
- 内积空间（pre-Hilbert space/欧几里得空间）
- 范数（norm）
- 范数和距离（distance）
- 偏差方差权衡（Bias - Varience Tradeoff)
- 凸函数（convex function）
- 原问题和对偶问题（primal vs dual）
- python实现
- 参考资料
支持向量机的背景介绍
- support vector machine
- 思想直观，但细节复杂，涵盖凸优化，核函数，拉格朗日算子等理论
- 二分类模型，也可用于回归分析
- 最基本表达形式是线性约束的凸二次规划问题，有最优解
核心思想
- 策略：间隔（margin）最大化，最不受到噪音的干扰
- 间隔和软间隔
- 超平面唯一（距离超平面最近的几个点为支持向量（support vector））
- （-1， 1） 0
- 带着以上关键词来理解支持向量分类器，过程如下
- 假设有一种新药物进行小鼠药性实验，药效如下图：坐标轴为药效，所有的点是输入的数据，红色表示药效很差，绿色表示药效很好。现在的目的就是：输入新的药效数据，判断它是好是坏。
- 如果简单的把分界点放在药效最差的最大值是不合理的。如下图，橙色的线表示的是此时的分界点，在此分界点左边的就是药效差，右边就是药效好。当出现新的观测值（黑点）时，由于它处于橙线右侧，所以它被判定为药效好。可实际上，它离药效差的点明明更近，他应该被归为药效差的一类。同理，把分界点放在药效最好的最小值也是不合理的：
- 在以上的基础上，我们能不能把分界点设置在橙点极大值和绿点极小值的中间呢，如下图所示，当出现一个新的黑点时，我们很容易就把它归为药效差的那一组，这样看着也挺合理的：
此时，橙点最大值、绿点最小值 和 分解点之间的距离，称为间隔（margin），如下图橙色虚线和绿色虚线所示，间隔最大化对数据集的橙点和绿点才公平，而此时的间隔称为硬间隔，它所对应的数据是线性可分的：
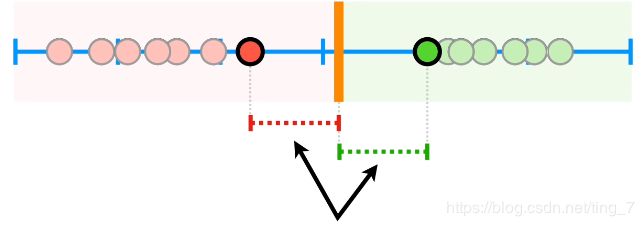
- 但是，如果数据集是下面这张图这样呢？
可以看到：有一个橙点的离群值，虽然它药效不好，但是离药效好的那些点特别近。
此时，允许间隔最大化的分界点离绿点超级近，但是离大多数橙点都超级远
在这种情况下，如果出现了一个新的黑点，即使它离药效好的点很近，也会被判定为药效差：
总结：最大间隔化受训练集异常值的影响非常大。 - 那么，如何让最大间隔化对异常值不那么敏感呢？我们需要允许误分类。通过偏差-方差权衡，就可以选择一个恰当的分界点。
当允许误分类时，分界点和观察点之间的距离，不再称为间隔，而是软间隔（严格来讲，软间隔对应的是线性不可分的情况，但这里因为有明显的异常值，所以还是将其引进）。我们可以通过交叉验证来决定分界点，在此基础上看看多少误分类被允许，确定软间隔的大小，并最终得到最合适的分类器。 - 软间隔分类器就是支持向量分类器，支持向量指的是位于软间隔边缘和内部的观测值，如下图所示
- 以上是一维线上的例子，它的分界点是一个点；如果是二维平面上，那分界就是一维的线；如果是三维空间中，那分解就是二维的线；如果是四维，比如我们加上时间这个维度，那分界就是某个时间点的三维空间，也就是超平面。严格来说，所有的分界，都可以称为超平面。
公式和SVM分类
公式
超平面公式
先看看两个简单的超平面： 二维超平面
三维超平面
d维空间的超平面和二维三维都是一样的，d维空间的超平面维度为（d-1），其超平面公式如下：
其中，ω是超平面的法向量（d维上的列向量），它决定超平面的方向（法向量指向的那一面是它的正面, 另一面则是它的反面）。f(x) = ω * x -b
x也是d维上的列向量，它指的是需要分类的点
ω和b都是超平面参数，b是超平面和原点之间的距离
公式推导
距离公式：和高中点到直线的距离公式基本一样（这里平方写在右下角，意思是一样的）
对于下图公式我的理解：
第一个和第二个公式是根据点到平面距离公式推出来的，为了实现间隔 ω* 最大化，先挑选距离超平面最近的支持向量，计算它们和平面的距离，然后从这些最近的点中挑选最大的距离就是最大间隔。但此时的间隔为函数间隔，它受参数ω和b的影响，如果它俩翻倍，此时超平面还是原来的那个超平面，但间隔会变小。所以说这个间隔不靠谱，需要升级为几何间隔。
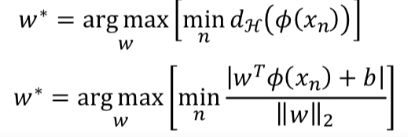
第三个公式中，把ω模的平方拿出来，方便后面计算
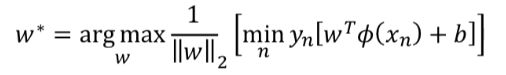
其中
为了方便求解，令：y * f(x) = 1 。比如下图中 s.t = subject to ，表明约束条件就是 y * f(x) = 1
通过以上的推导得到以下的原问题：
当 C = 0 时，边界没有那么复杂
当 C = inf ,即为任意数字时，边界复杂度提高
由于约束条件在电脑中不是那么方便模拟，所以需要转为对偶问题去求。给约束条件加上一个拉格朗日对偶λ，让原函数和约束条件共同组成一条新的函数，此函数包含ω，b, λ这三个参数
经过层层推导
过程太长了不看了，可以得到这最终的对偶问题
归一化后的超平面公式
如果使用归一化或标准化的数据集，则超平面公式为：
- 当 ω * x ≥ 1 时，归为一类，这一类的标签是1
- 当 ω * x ≤ -1时，归为另一类，这一类的标签是-1
如果像我平时做的话是要做归一的，因为我有很多的种类数据，数据的单位不一样，而且有些数据特别大，有另外一些数据都是小数点，这样不归一的话结果就会很诡异了
SVM分类
1. 线性SVM：
- 硬间隔SVM：数据线性可分，没有显著的离群点
在硬间隔中，最靠近超平面的 x 向量，就是该超平面的支持向量，这些支持向量决定了超平面实现间隔最大化。
- 软间隔SVM（数据近似线性可分，比如上文有一个异常的离群值，但是被误分类掉，这个时候需要引进铰链损失函数）。
二. 非线性SVM
引进核函数，分类器在原始输入空间中是非线性的，但在变换后的特征空间中，支持向量机可以拟合出最大间隔超平面。
详见下文核函数部分。
三. 损失函数
由于软间隔分类器的数据线性不可分，所以引进hinge loss，公式如下：
其中的y是分类器的原始输出，而不是预测的标签，所以公式也可以写为：
当（1）满足时，xi位于间隔正确的那一面，则该函数为零：
对于间隔的错误一侧的数据，该函数的值与距间隔的距离成正比。 然后我们希望最小化
（此处，λ用来权衡增加间隔大小与确保xi位于间隔的正确一侧之间的关系)
因此，对于足够小的λ值，如果输入数据是可以线性分类的，则软间隔SVM与硬间隔SVM将表现相同，但即使不可线性分类，仍能学习出可行的分类规则。
注意：hinge loss不是可微函数，而是一种凸函数，它保持了支持向量机解的稀疏性。正是因为hingeloss的零区域对应的正是非支持向量的普通样本，从而所有的普通样本都不参与最终超平面的决定，这才是支持向量机最大的优势所在，对训练样本数目的依赖大大减少，而且提高了训练效率。
核函数（kernel trick）
核心思想
- 核函数只是在希尔伯特空间中描述每对点的联系【包括：点与点之间的距离、对应协方差（即两个变量如何相关变化）】，但它不会做直接的转换。简单讲就是核函数只计算更高维的数据的联系，而不负责把数据转换到更高维，所以不能简单的理解为低维到高维的映射。（这也算是英文名字的由来我感觉，因为trick相当于作弊一样，他没有算最后的数值，而直接计算点间联系）
- 核函数具体功能，是在解SVM对偶问题的最优化问题时，能够使特征向量φ(x)更方便地计算出来，特别是φ(x)维数很高的时候。
为什么要把核函数和SVM结合起来？
- 首先，核函数可以不用让SVM将数据从低维到高维进行转换，它可以直接计算高维数据的联系，这可以大大减少支持向量机的计算量。
- 其次，它可以帮助非线性的数据在更高维的空间构造超平面。
上文核心思想的第七点讲到：所有维度的分界都可以称之为超平面，而且就算有离群的异常值，数据仍然是线性可分的，比如核心思想的第五点，只是它如果太简单粗暴的直接拿中点构建超平面的话不太合理，才采用了软间隔SVM。
接下来这个例子，才是真正的数据非线性，如图，橙点依旧表示药效差的数据，绿点表示药效好的数据。可以看到，服用的剂量过高或过低，都会导致药效变差：
在这种情况下，在这条一维的线中，根本无从下手对超平面进行构造，此时我需要引进核函数，来帮助我计算数据高维形式时的联系。
本例中使用多项式核函数，图中横轴依然时药物剂量，但是纵轴取了药物剂量的二次方，因此很容易地构建超平面，将药效好和差地点分开，当出现预测点（黑点后），也顺应地被分到了超平面的上面，即药效差的那一侧。
kernel支持向量机的简单流程
一. 输入低维数据
二. 将数据从低维到高维进行转换
注：怎么样的转换方式是最合适的？（比如上文为何对数据二次方，而不是三次方，也不是开方后再乘以一个系数）
核函数包括多项式核函数和径向基核函数。比如上文就是用了多项式核函数，多项式核计算了上面二维空间中每一对观测值的关系，而这些关系就被用来寻找合适的SVC。上图的项数d = 2，可以接着增加项数到3，等等，然后最后交叉验证可以发现最合适的d
第二种核函数——径向基核函数，用于无限维的空间，而在上图的这个例子中，如果使用径向核，它发挥的功能和加权近邻其实很像。比如我输入一个新的观测值，它最终被分类到药效好或者坏的那一组，会非常严重的受离它最近的点的影响，距离比较远的话，对它的影响相应就小一些。
三. 通过交叉验证选择最合适的支持向量分类器
常见的核函数及其应用
一. 多项式核函数
二. 高曲双切核函数（神经网络）
三. 高斯径向基核函数（无限维，一般数据没有先验知识就可以用这个）
名词介绍
希尔伯特空间（Hilbert space）
由若干个函数作为独立坐标构成的抽象空间。
内积（inner product）
①向量的内积：
- 测量向量之间的相似性
- 对于两个向量x和y，内积是一个向量到另一个向量的投影
如果 x = (x1,x2,…,xi), y = (y1, y2, …, yi)
②函数的内积：
因为函数由无限的向量组成（当Δx --> 0时），所以函数和向量一样都可以内积。
对于函数f(x)和g(x)，
③向量和函数的不同之处：向量的维度是离散的，我们只有一维、二维、… 、N维向量（N为整数集），没有0.5维，1.5维这些，但是函数的维度是连续的，所以需要用相邻维度之间的不同（比如说Δx）来归一化。
归一化和标准化（normalization vs standardization）
这两种处理都是对数据进行特征缩放
- 归一化：数据归一化后属于(0, 1)或（-1， 1），
- 极值归一化（0， 1）
- 均值归一化（-1，1）
- 极值归一化（0， 1）
一般数据比较稳定，极值不太夸张，或者不知道极值的具体数值，都可以用归一化
- 标准化：数据标准化后符合μ = 0， σ = 1的正态分布
- 标准差标准化（z-score标准化）（提供了原数据的均值和标准差）
一般异常值和噪音太多用标准化
内积空间（pre-Hilbert space/欧几里得空间）
内积空间称为准希尔伯特空间是有他的道理的，因为刚刚上面提到希尔伯特空间是由函数组成的，函数上的点是连续的，但向量是离散的，那在线性空间上定义内积的这个空间就是成为希尔伯特空间的前一步，这个空间就称作内积空间。
范数（norm）
- 定义：向量在内积空间中的“长度”
范数和距离（distance）
- 差异
- 常用距离（竟然发现有我专业里常用的，学这个还是有点用的。。）
-
Bray-Curtis 相异度，它可以用来用来衡量不同样地物种组成差异的测度，公式如下
-
Pearson相关距离
注：ρ（X, Y)是皮尔森相关系数，公式如下：
-
-
欧几里得距离（直线距离，最短）
-
余弦相似度距离：通过测量两个向量的夹角的余弦值来度量它们之间的相似性
-
曼哈顿距离：两个向量在标准坐标系上的绝对轴距总和
下面这个图能非常明显地将欧几里得距离、余弦相似度距离和曼哈顿距离区别开
偏差方差权衡（Bias - Varience Tradeoff)
1.定义（偏差/方差）
偏差：通过学习拟合出来的结果的期望，与真实结果之间的差距。可以通过提高模型的复杂度来降低偏差，但参数过多、模型过于复杂会导致过拟合
方差：通过学习拟合出来的结果自身的不稳定性，也就是不同训练集输出结果的差异
2.定义解释：
-
输入以下数据集，目的是得出身高体重的相互关系
-
将数据分成两组，以下蓝色的点代表训练组（train set），绿色的点代表测试组（test set）。因为是随机分组的，所以可以分很多次，可以有很多个训练组。
-
先用线性回归学习一下，但是线性回归的这条直线无论怎么调试，也不能捕获到身高和体重之间正确的关系。模型输出的结果，和真实样本之间的差异称为偏差。因为线性回归模型的这条直线和真实样本的关系“线”差距很大，所以线性回归模型的偏差就很大。
-
既然直线偏差这么大，那就直接上曲线，把每个点都包含在内，这样偏差就是最小的，是为0
-
如果只比较训练集和真实样本的偏差的话，曲线的这个模型是比线性回归模型更好的。但是如果用刚刚第二个数据集（测试集）来验证，会发现线性回归模型的偏差更小
-
就算曲线模型的偏差用测试集来验证之后发现很小，但是，当输入不同的训练集的时候（如第一点所说，训练集可以有很多个），就会生成很多不同的曲线，这些曲线是不同的模型，它们最终输出的结果也有很大不同。衡量所有训练集输出的所有结果之间的差异，就称之为方差。
3.如何实现权衡
- 从上面直线和曲线的区别可以知道：直线虽然偏差大，但方差小；曲线虽然偏差小，但方差大。换句话说，直线给出的预测可能不是和真实值最接近的，但却是最稳定的。另外，曲线虽然和训练集对应的很好，但和测试集相差甚远，这种情况称之为过拟合。
- 训练一开始，偏差很大，方差很小，因为模型太简单（比如上面那根直线）；但是随着参数的调试和训练次数的增加，偏差降低，方差增大，二者分别形成的曲线的交点就是权衡点。
凸函数（convex function）
维基百科的图感觉有点复杂，但其实它表达的意思和高中数学函数的中点问题基本一个意思，所以我把两个图都放出来方便理解。
凸函数的性质
（1）如果f(x)是凸函数，那-f(x)凹函数
（2）如果满足以下条件，则为凸函数：
（3）在f(x)是凸函数的前提下，如果满足以下条件（最多只有一个最值），则为严格凸函数：
注：***X***是凸集，凸集中任意两个点的连线都被包含在该凸集中。
原问题和对偶问题（primal vs dual）
（1）通常对偶问题指拉格朗日对偶问题
（2）下面这个图很常见到了，红线是原问题的图，蓝线是对偶问题的图。解决对偶问题最优原始解决方案带来一个下限。左边强对偶是因为原问题的最优解就是对偶问题的最优解，右边弱对偶是因为两个最优解之间还有对偶间隙，
python实现
后期爬一下专业文献的数据再来填坑
参考资料
机器学习里的 kernel 是指什么？
如何通俗的解释希尔伯特空间，它具有特别的性质么，如果有是什么？
归一化和标准化以及欧氏距离
向量和距离
Bias and Variance
偏差-方差权衡
Linear Support Vector Machine
怎么样理解SVM中的hinge-loss？
SVM（二）：从凸优化聊到SVM对偶式的推导
Support Vector Machines - THE MATH YOU SHOULD KNOW