感知机学习算法的拓展---非线性可分数据问题

感知机算法中的优化方法的几何解释

本部分参考台湾大学林轩田教授机器学习基石课程—PLA部分

PLA算法只有在出现错误分类的时候，才去调整w和b的值，使得错误分类减少。假设我们遇到的数据点(xn,yn)是我们第t次分类错误，那么就有因为是二分类问题，所以只会出现以下两种错误分类的情况：

• 第一种：当yn=+1 时，则我们的错误结果为wTxn=wt∗xn=||w||∗||xn||∗cosΘ<0，即cosΘ<0 则Θ太大,为了能过纠正错误，决定减小Θ，就让w(t+1)=wt+x,紫色为改正之后的w(t+1)
• 同理，对于第二种情况，当yn=-1的时候，则我们的错误结果为wTxn=wt∗xn=||w||∗||xn||∗cosΘ>0，即cosΘ>0 则Θ太小,为了能过纠正错误，决定增大Θ，就让w(t+1)=wt-x,紫色为改正之后的w(t+1)。

综上所述，当分割线遇到点(xn,yn)时，如果分割正确，那么wt就不变，如果分割错误，那么就令
（注意w是分割线wTx=0的法线，也就是说分割线的方向是与w的方向垂直的。。。）

思考

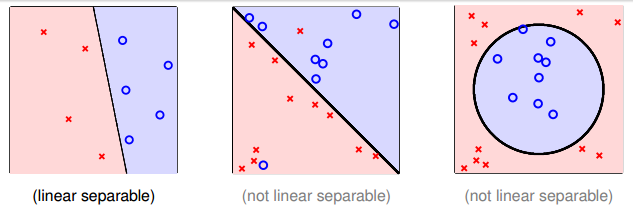
PLA 的优点是算法思路比较简单，易于实现。然而这个算法最大的缺点是假设了数据是线性可分的，然而事先并无法知道数据是否线性可分的。假如将PLA 用在线性不可分的数据中时，会导致PLA永远都无法对样本进行完全正确分开从而陷入到死循环中。
如下图所示，当实例点并不是线性可分的时候，根本找不到一条直线或者一个超平面来完全划分开两类数据，只能利用曲线或者超曲面来划分。

为了避免上面线性不可分的情况，将PLA的条件放宽一点，不再要求所有的样本都能正确的分开，而是要求犯错误的样本尽可能的少，即将问题变为了：

也是就是说去寻找一条犯错误最少的线或者超平面。

其实，从实际意义上，是不能的。这是一个著名的NP hard 问题！！！因为线有无穷多个啊！！！无法求得其最优解，因此只能求尽可能接近其最优解的近似解。林教授的课程讲义中提出的一种求解其近似解的算法 Pocket Algorithm（口袋算法，一种贪心算法）。

Pocket Algorithm（口袋算法）

口袋算法基于贪心的思想，他总是让遇到的最好的线（或者超平面）拿在自己手里。简单介绍一下：首先，我们有一条分割线wt，将数据实例不断带入，发现数据点(xn,yn)再上面出现错误分类，那么我们就纠正分割线得到w(t+1)，然后我们让wt和w(t+1)遍历所有的数据，看一下哪条线犯的错误少，那么就让w(t+1)代替wt，否则wt不变。

那么如何让算法停下来呢？

由于口袋算法得到的线越来越好（PLA就不一定了，PLA是最终结果最好，其他情况就不一定是什么样子，不一定是越来越好），所以我们就自己规定迭代的次数。

思考？

答案是：PLA更好。先不说PLA可以找到最好的那条线。单从效率上来说，PLA也更好些。最主要的原因是，pocket algorithm 每次比较的时候，都要遍历所有的数据点，且两个算法都要遍历一遍，才会决定那个算法好，而这还是比较一次，如果我们让他迭代500次的，那就麻烦了！！！但是，所有前提是，数据是线性可分的。如果线性不可分，只能用pocket algorithm，因为PLA根本不会停下来（而且PLA的wt也不是每更改一次效果就会比之前的好）！！

与PLA的比较：

1、Pocket Algorithm事先设定迭代次数，而不是等着算法自己收敛到最优。
2、随机遍历数据集，而不是循环遍历。
3、遇到错误点校正时，只有当新得到的w对于所有的数据优于旧w的时候（也就是整体错误更少的时候）才更新，而PLA算法中，只要出现错误分类就更新。由此也可知，pocket Algorithm算法是保证每次得到的线或这面是越来越好的，而PLA算法不一定。而且，由于Pocket要比较错误率，需要计算所有的数据点，因此效率要地域PLA。所以在线性可分的数据集上，使用PLA算法，而不选择使用Pocket算法。但是，只要迭代次数足够多，Pocket和PLA的效果是一样的，都能够把数据完全正确分开，只是速度慢。

代码实现

下面，我们用Python来实现pocket Algorithm算法。

# -*- encoding:utf-8 -*-
'''
@author=Ada
Python实现的pocket algoritm
'''

from numpy import vectorize
import numpy as np
import matplotlib.pyplot as plt

class Pocket:

    def __init__(self,random_state=None):
        self.numberOfIter=7000#最大迭代次数
        self.minWeights=None
        self.intercept=None#bias 截距
        self.errorCountArr=np.zeros(7000)#统计每次迭代的出错数
        self.errorCount=[]#统计每次优化或者每个更新权值时候的出错次数
        self.minErrors=7000#出错数量的初始值，一开始一般设置一个比较大的值
        self.random_state=random_state

    def predict(self,z):
        if z<0:
            return -1
        else:
            return 1

    def checkPredictedValue(self,z,actualZ):
        if(z==actualZ):
            return True
        else:
            return False

    def fit(self,X,Y):
        row,col=X.shape
        weights=np.array([1.0,1.0,1.0,1.0])
        vpredict = vectorize(self.predict)
        vcheckPredictedValue=vectorize(self.checkPredictedValue)
        learning_rate=1.0
        bias_val=np.ones((row,1))
        data=np.concatenate((bias_val,X),axis=1)
        np.random.seed(self.random_state)
        count=0
        iter=0
        while self.numberOfIter>0:
            weightedSum=np.dot(data,weights)
            predictedValues=vpredict(weightedSum)
            predictions=vcheckPredictedValue(predictedValues,Y)
            misclassifiedPoints=np.where(predictions==False)#分类错误的数据
            misclassifiedPoints=misclassifiedPoints[0]
            numOfErrors=len(misclassifiedPoints)#分类错误的数据量
            self.errorCountArr[iter]=numOfErrors
            if numOfErrors1
            iter+=1
            misclassifiedIndex=np.random.choice(misclassifiedPoints)#这一步与PLA不同，
                                                                    # 在此是随机从错误数据点里面选择一个点，进行更新权值
            weights+=(Y[misclassifiedIndex]*learning_rate*data[misclassifiedIndex])
            self.numberOfIter-=1
        self.weights=weights[1:]
        self.intercept=weights[0]

def main():
    data=np.loadtxt('classification.txt',dtype='float',delimiter=',',usecols=(0,1,2,4))
    X=data[:,0:3]
    Y=data[:,3]
    p=Pocket(random_state=2308863)
    p.fit(X,Y)
    print "Weights:"
    print p.weights
    print "Intercept Value:"
    print p.intercept
    print "Minimum Number Of Errors:"
    print p.minErrors
    ax1=plt.subplot(121)
    ax1.plot(np.arange(0,7000),p.errorCountArr)
    ax2=plt.subplot(122)
    ax2.plot(np.arange(0,len(p.errorCount)),p.errorCount)
    plt.show()

if __name__ == "__main__":
    main()

实验结果：Weights:[-0.43701921 -0.10683611 0.34784736]
Intercept Value: -1.0
Minimum Number Of Errors:935

上图的第一幅表示的是每次迭代时的出错数，第二幅图表示的每次更新权重时的出错数。通过上图可以观察到，在7000次迭代过程中，每次迭代出错数是不固定的，而每次更新时出错数是递减的。而且，7000词迭代过程中只有十次左右的更新操作。

参考资料：

1、机器学习基石—PLA
2、台湾大学林轩田教授机器学习基石课程理解及python实现—-PLA
3、分类系列之感知器学习算法PLA 和 口袋算法Pocket Algorithm
4、听课笔记（第二讲）： Perceptron-感知机 (台湾国立大学机器学习基石）

《完》

人生如棋，落子无悔！
                       ------- By Ada